中学の図形証明問題(合同･相似)の解き方と証明の書き方ポイント

図形の証明問題の解き方と証明の書き方のポイントをお伝えします。
中学の数学での図形の証明問題は合同か相似を利用することがほとんどです。
長さが等しいことや角度が等しいことを示すのも合同か相似を証明してからになります。
ここでは合同と相似の証明のポイントをまとめておきますので確認しておきましょう。

図形の証明を書くときのポイント

図形の証明をするときには、
証明を書き出す前にすることがあります。

ここが一番のポイントだといっても良いくらいですよ。

イメージをつかむためにまずは簡単な例題を見ておきましょう。

「長さが等しい」ことを証明する問題なので、
三角形の合同を先に証明します。

「合同な三角形では
対応する辺と角がすべて等しくなる」
ことを利用できるからです。

合同を使わず長さが等しいことを証明するということはありません。

例えば三平方の定理を使って具体的な長さを求めて、
それが等しいことをいう場合は
「長さを求めなさい。」
という問題になりますので、
線分の長さが等しいことを示す場合は『合同』だと考えておくとはやいです。

この問題の条件を書きだしてみると、

　\(\,\mathrm{AB=BC=CA}\,\)
　\(\,\mathrm{BP=AQ}\,\)

だけだと思った人はいませんか？

図形問題全般に言えることはそこです。
「そこってどこよ？」
という声が聞こえて来そうですが、
等号などがついた条件式や具体的な数値だけが
問題の条件だと思っている人が多いということです。

日本語で書かれている条件を見逃し、
条件が上の２つであると思っている人は証明ができません。
合同を示すには条件が足りないからです。

最初から問題を読んでいきますが、
ポイントになるのは条件を図示することです。
図示するというのは図に書き込むということですよ。

ここでは何を読み取り切れていないかというと、
“四角形\(\,\mathrm{ABPC}\,\)は円\(\,\mathrm{O}\,\)の周上”という言葉です。

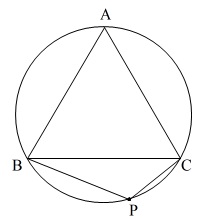
“円\(\,\mathrm{O}\,\)の周上”とあれば、何を思いだしますか？
そうです。

半径が等しいということは当然ですが、
加えて『円周角の定理』です。
※
まだ習っていない人は気にしないでください。
ポイントは定理を知っているかではありませんので。

まずは問題文の順に図示していくことにして、
円周角については後で加えましょう。

具体的な数値である角度についての条件が
問題に書かれていないので見逃してしまうことが多いですが、
　\(\,\mathrm{BA=BC=CA}\,\)

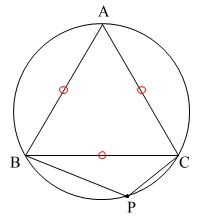
という条件から、
三角形\(\,\mathrm{ABC}\,\)が正三角形と分かるので、
　\(\,\mathrm{∠ABC=∠BCA=∠CAB=60^{\circ}}\,\)
というのも分かりますが、
問題文の次に移りましょう。

「点\(\,\mathrm{Q}\,\)は弦\(\,\mathrm{AP}\,\)上にあって、
\(\hspace{10pt}\,\mathrm{BP=AQ}\hspace{4pt}\,\)」
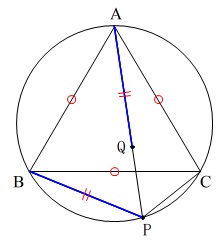さらに、
四角形\(\,\mathrm{ABPC}\,\)が“円\(\,\mathrm{O}\,\)の周上”ということから、
弧\(\,\mathrm{PC}\,\)（または弦\(\,\mathrm{PC}\,\)）の円周角となる
　\(\,\mathrm{∠PBC=∠QAC}\,\)
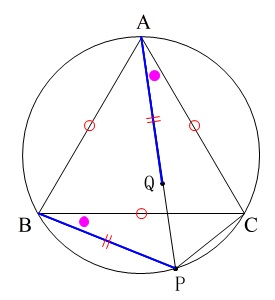も言えることになります。

ここまでの条件を図に書き込んでみて下さい。
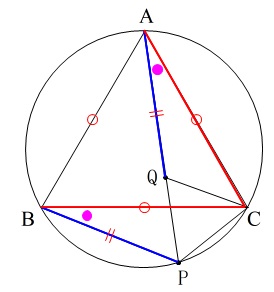明らかではありませんか？
すでに合同を証明出来ていることに気が付くと思います。

証明は
　\(\,\mathrm{BC=AC}\,\)（仮定）
　\(\,\mathrm{BP=AQ}\,\)（仮定）
　\(\,\mathrm{∠PBC=∠QAC}\,\)（弧\(\,\mathrm{PC}\,\)の円周角）

から三角形の合同条件
　『２辺とその間の角がそれぞれ等しい』
が言えるでしょう。

　\(\,\mathrm{△BPC}　≡　\mathrm{△AQC}\,\)

「合同な三角形では対応する辺と角がすべて等しくなる」
ので
　\(\,\mathrm{CP=CQ}\,\)
が証明できました。

図形の証明を書く前にすること、
それは『図の中で証明を終わらせるほど条件を図示する』ということです。

合同の証明の書き方と合同条件

合同の証明はたくさん練習しているでしょう。
ここでは解答の流れと書き方だけ簡単に説明しておきます。

先ず合同を証明したい2つの三角形を書きます。

　\(\,\mathrm{△ABC}\,\)と\(\,\mathrm{△DEF}\,\)において

ここから示していくのは合同条件をいうために必要な条件です。

三角形の合同条件は5つあります。
ここでは取り上げませんので『覚え太郎』で確認しておいて下さい。

注意点は、最初に書いた2つの三角形で、
　左に書いた三角形の辺や角は左辺に
　右に書いた三角形の辺や角は右辺に
書いていくことです。

　\(\,\mathrm{\color{red}{△ABC}}\,\)と\(\,\mathrm{\color{blue}{△DEF}}\,\)について
としたなら
　\(\,\mathrm{\color{red}{AB}=\color{blue}{DE}}\,\)
　\(\,\mathrm{\color{red}{∠ABC}=\color{blue}{∠DEF}}\,\)
のように
　左辺には左に書いた\(\,\mathrm{△ABC}\,\)について
　右辺には右に書いた\(\,\mathrm{△DEF}\,\)について
書き並べていくということです。

合同条件をそろえます。

基本的な証明は、

　\(\,a=b　(仮定)　･･･①\,\)　
　\(\,c=d　(仮定)　･･･②\,\)
　\(\,\color{red}{e}=\color{blue}{f}　(理由)･･･③\,\)
　\(\,\color{magenta}{g}=\color{blue}{f}　(理由)　･･･④\,\)
③④から
　\(\,\color{red}{e}=\color{magenta}{g}　･･･⑤\,\)
①②⑤から
　合同条件の1つが成り立つので
　
という流れです。

書き方は、
　
仮定より
　\(\,a=b　･･･①\,\)　
　\(\,c=d　･･･②\,\)
また、　
(理由)から
　\(\,\color{red}{e}=\color{blue}{f}･･･③\,\)　
(別の理由)から
　\(\,\color{magenta}{g}=\color{blue}{f}　･･･④\,\)

と日本語をうまく使って論理的に組み立てても良いですが、
(理由)を条件の後ろに付け足しても良いです。

(理由)が長くなるときは両方を組み合わせて書いても良いです。
条件と理由が書いてあれば
自分が書きやすい方でかまいません。

条件を図示することができていれば、
証明すべき内容は図の中で完成しているので、
それを書き出していくだけです。

図の中ですら示せていないことは証明できるはずはありません。

図示しても合同条件が見つけにくいときは、
「合同条件5つのうちで言える条件はないか」
を逆に探すという方法もあります。

図示するを忘れている条件に
気づかせてくれることがあるので試して見ると良いですよ。

相似の証明の書き方と相似条件

相似の証明方法や書き方は合同と同じです。

合同は相似な図形の相似比が\(\,1:1\,\)のとき
のことをいうので同じでないとおかしい。
ただし、相似の方が範囲が広いので条件はゆるいです。

相似条件3つは確認しておいて下さい。

図示して
相似条件を図の中で確認してから証明を書き始める
というポイントは合同のときと同じですよ。

相似は高校になると証明しません。
見抜いて当たり前となります。

相似を見抜いて（証明して）その後の問題を解く
というのは高校入試でも同じなので
相似の証明そのものと、
その後の使い方は多めに練習しておくと良いです。

もし、証明できなくても、
その後の問題は「証明できた事実」として利用するのを忘れないでください。

証明できていないから次の問題は採点基準にならない、ということではありません。

証明問題の基本と応用の違いは？

数学の問題には問題作成者がさりげなく隠したヒントがあります。

さりげない条件とは「平行四辺形」という言葉もそうですし、
他にもたくさんあります。

あなたが
「なんでこの問題が解けないのか」
そう悩んだときは、
問題作成者が出してくれている条件が使い切れていないからです。
（基本的な定義や定理は覚えていることが前提ですよ。）

⇒　全国の公立高校入試 数学過去問の解答解説

全国の公立入試過去問から解けない問題を探してみてください。
「すべて解ける。」
というほど解けない問題が無ければ基本ができているということです。

それまでは、
「解けないのは条件が使い切れていないからだ」
と思っておいて下さい。

応用問題は
かくされた条件が１つか２つ多いだけ
なのですよ。

長くなるのでここでは具体的な問題は取り上げませんが、
上で証明した問題では仮定が2つ使えましたが、
仮定が1つだけ使えてつながる条件が2つ、
という場合などがそうです。

合同、相似の証明問題ではどのような場合も、
合同条件や相似条件を満たすように
理由と条件ををそろえる
という流れは同じです。

それから、
普段から図はできるだけ自分で書くようにすると
問題の意味が分かり易くなります。

上で取り上げた問題も簡単に条件だけを書き加えると
となりますが、
書いて見ると意外と簡単に合同条件は見つかるでしょう。

中学生の場合は問題に図が与えられることが多いですが、
自分で書くと問題の条件が足りていない部分はすぐにわかります。
試験の時は時間節約のため与えられた図を利用しても良いですが、
演習のときは自分で図を書くことをお勧めします。

図を書くというのは、
数学の問題を解く際に必要な作業では基本中の基本です。

やってもらえればわかります。
この作業を続けるとあなたの数学の力は確実に上昇します。

条件を見逃せば答えは求まらない。
それが数学の問題なのです。

⇒　中学生ができる数学の応用問題の解き方と解けるようになるコツ

中学、高校の数学全般に言えることですので、
知っておくだけでも変われます。

クラブ活動で忙しい！
塾に通っているのに数学が苦手！
数学の勉強時間を減らしたい！
数学の勉強方法が分からない！

その悩み、『覚え太郎』が解決します！！！