秋田県で2018年(平成30年度)に行われた公立高校入試の数学の第5問-1の解説です。
第5問は学校指定の選択問題になるますが5－2とともに関数と確率の融合です。
前半は関数の基本問題なので確実に得点しておいて、後半の確率は時間配分を考えてチャレンジになりますが、格子点を数え上げればもはや算数に近いです。
問題は秋田県の公式サイトにもあります。
\(\,\large{5-Ⅰ}\,\)
『指示された問題について答えなさい。』
と問題にあります。
受験する学校によって指定されますので秋田県の受験生は間違えないようにしましょう。
良い問題なので他県の受験生は参考にしておくと良いです。
問題に与えられている条件です。
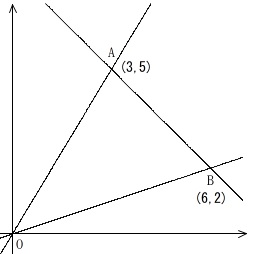
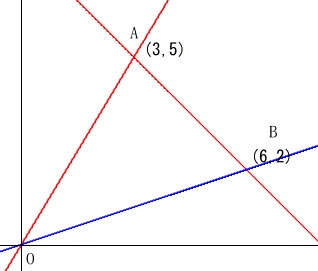
\(\,\mathrm{A\,(\,3\,,\,5\,) , B\,(\,6\,,\,2\,)}\,\)
直線ア：\(\,2\,\)点\(\,\mathrm{A,B}\,\)を通る
直線イ：原点\(\,\mathrm{O}\,\)と点\(\,\mathrm{A}\,\)を通る
直線ウ：原点\(\,\mathrm{0}\,\)と点\(\,\mathrm{B}\,\)を通る
一挙に最後まで答えを出したい、というはやる気持ちをおさえて解説します。
ちなみに短時間で処理するとどれくらいで終わるか、
ここを読んでくれている人に特別にお見せしておきます。
私じゃなくて『超え太郎』マスターの中学生ですよ。
(1)
直線アは\(\,2\,\)点\(\,\mathrm{A,B}\,\)を通るので
\(\begin{eqnarray}\displaystyle
y-5&=&\frac{\,2-5\,}{\,6-3\,}(x-3)\\
&=&-1(x-3)\\
y&=&-x+8
\end{eqnarray}\)
（答え）\(\,\underline{ y=-x+8 }\,\)
(2)
\(\begin{eqnarray}\displaystyle
\mathrm{△AOB}&=&\frac{|\,3\times 2 -5\times 6\,|}{2}\\
&=&\frac{|\,6-30\,|}{2}\\
&=&12
\end{eqnarray}\)
（答え） \(\,\underline{\mathrm{ 12\,cm^2 }}\,\)
(3)\(\,\mathrm{△ABC}\,\)内にある格子点\(\,(m,n)\,\)について
\(\,m=1\,\)のとき\(\,n=1\,\)
\(\,m=2\,\)のとき\(\,n=1,2,3\,\)
\(\,m=3\,\)のとき\(\,n=1,2,3,4,5\,\)
\(\,m=4\,\)のとき\(\,n=2,3,4\,\)
\(\,m=5\,\)のとき\(\,n=2,3\,\)
\(\,m=6\,\)のとき\(\,n=2\,\)
の\(\,15\,\)点あるので
\(\displaystyle \frac{15}{36}=\frac{5}{12}\)
（答え） \(\,\displaystyle \underline{ \frac{5}{12} }\,\)
普通の過去問解説とかはこれくらいで済んでるのでしょう。
楽で良いですね。笑
こんな解き方は一般には役に立たないので解説します。
(1)
\(\,2\,\)点\(\,\mathrm{A\,(\,3\,,\,5\,) , B\,(\,6\,,\,2\,)}\,\)
を通る直線アを求めます。
\(\,(\,3\,,\,5\,)\,\)
\(\,(\,6\,,\,2\,)\,\)
から変化の割合を求めます。
求める直線は定直線ではなく\(\,1\,\)次関数になるので変化の割合が傾きに一致します。
\(\displaystyle \color{red}{(傾き)=(変化の割合)=\frac{ y\,の増加量 }{ x\,の増加量 }}\,\)
増加量を求めるときは、引く方向を変えると傾きの符号が変わりますので、
\(\,x,y\,\)ともに同じ方向に引きます。
このサイトでは下から上を引くと統一しています。
『求める直線の傾きは
\(\,2\,\)点\(\,\mathrm{A\,(\,3\,,\,5\,) , B\,(\,6\,,\,2\,)}\,\)
を通ることより
\(\,(x\,の増加量)=\,6-3\,=\,3\,\)
\(\,(y\,の増加量)=\,2-5\,=\,-3\,\)
から傾きは
\(\displaystyle \frac{-3}{3}\,=\,-1\)
このとき求める直線は
\(\,y=-x+b\,\)
とおけて、\(\,\mathrm{A,B}\,\)を通るので』
どちらでも良いですが、どちらか代入すれば切片が求まります。
『\(\,\mathrm{A(3,5)}\,\)を代入すると、
\(\begin{eqnarray}
(5)&=&-(3)+b\\
5+3&=&b\\
8&=&b
\end{eqnarray}\)
よって
（答え） \(\,\underline{ y=-x+8 }\,\) 』
代入するときは正の値であろうが負の値であろうが（かっこ）をつけて置くと計算ミスは減ります。
『求める過程も書きなさい。』とあるので、『赤かっこ』部分を抜き出してまとめておけば十分です。
(2)\(\,\mathrm{△AOB}\,\)の面積を求めます。
上で示したように答えの直通の方法もありますが、中学生らしく解いて見ましょう。
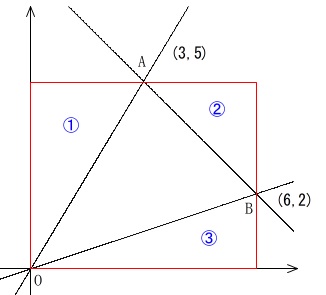図の赤い四角形は長方形で各点の\(\,x,y\,\)座標から縦と横の長さが分かります。
長方形から①②③の三角形の面積を引けば求める\(\,\mathrm{△AOB}\,\)の面積は求まります。
しかし、ここでは(1)を利用する方法を示しておきます。
何のために(1)(2)と続くのかを知っておきましょう。
(1)で\(\,\mathrm{AB}\,\)の方程式は
\(\,y=-x+8\,\)
と求めました。
これは\(\,y\,\)切片が\(\,8\,\)の直線です。
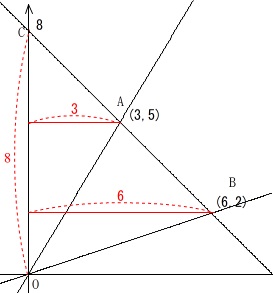この切片を\(\,\mathrm{C}\,\)としたときの\(\,\mathrm{OC}\,\)を底辺とする三角形を考えます。
三角形の高さは\(\,x\,\)座標からそれぞれ分かるので
\(\begin{eqnarray}\displaystyle
\mathrm{△AOB}&=&\mathrm{△OBC}-\mathrm{△OAC}\\
&=&\frac{1}{2}\times 8\times 6-\frac{1}{2}\times 8\times 3\\
&=&24-12\\
&=&\underline{ 12 \mathrm{(cm^2) }}
\end{eqnarray}\)
(3)
大小2つのさいころを同時に\(\,1\,\)回投げたとき、と1つずつ投げたときは同じことです。
大きいさいころの出た目を\(\,m\,\)
小さいさいころの出た目を\(\,n\,\)
とするとき、
座標\(\,(m,n)\,\)が\(\,\mathrm{△OAB}\,\)の周上を含む内部になる確率
を求める問題です。
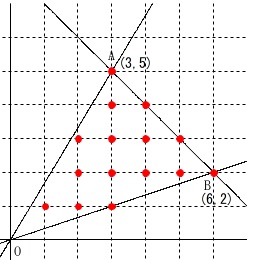この\(\,15\,\)点を探すのですが、内部にあるかは調べてみないと分かりません。
そのために直線\(\,\mathrm{OA}\,\)と直線\(\,\mathrm{OB}\,\)を求めておく必要があります。
直線\(\,\mathrm{OA}\,\)は原点を通るので
\(\displaystyle y=\frac{5}{3}x\,\)
直線\(\,\mathrm{OB}\,\)も原点を通るので
\(\displaystyle y=\frac{1}{3}x\,\)
座標で\(\,x,y\,\)ともに整数の点を格子点というのですが、
さいころを転がして出てきた出目は整数なので\(\,(\,m\,,\,n\,)\,\)は格子点で、
\(\,(\,m\,,\,n\,)\,\)が\(\,\mathrm{△AOB}\,\)の内部または周上にあるには
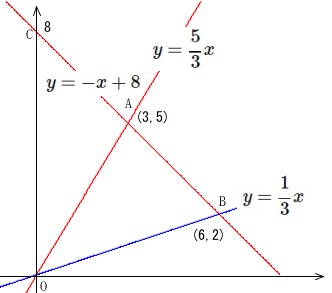
\(\displaystyle \color{blue}{y=\frac{1}{3}x}\,\)
以上で、(下限)
\(\displaystyle \color{red}{y=\frac{5}{3}x} かつ \color{red}{y=-x+8}\,\)
以下(上限)、
にあるかどうかを調べていけば良いのです。
下限を見るのは
\(\displaystyle y=\frac{1}{3}x\,\)
1つで良いですが、
上限を見るのは\(\,\mathrm{A(3,5)}\,\)なので
\(\,1≦m≦3\,\)は\(\,\mathrm{OA}\,\)の\(\,\displaystyle y=\frac{5}{3}x\,\)
\(\,4≦m≦6\,\)は\(\,\mathrm{AB}\,\)の\(\,y=-x+8\,\)
を見ます。
\(\,x=1\,\)のとき、
下限は \(\displaystyle y=\frac{1}{3}\times (1)=\frac{1}{3}\,\)
上限は \(\displaystyle y=\frac{5}{3}\times (1)=\frac{5}{3}\)
\(\,m=\color{red}{1}\,\)のときこれを満たすのは
\(\,n=\color{blue}{1}\,\)
\(\,x=2\,\)のとき、
下限は \(\displaystyle y=\frac{1}{3}\times (2)=\frac{2}{3}\,\)
上限は \(\displaystyle y=\frac{5}{3}\times (2)=\frac{10}{3}\)
\(\,m=\color{red}{2}\,\)のときこれを満たすのは
\(\,n=\color{blue}{1,2,3}\,\)
\(\,x=3\,\)のとき、
下限は \(\displaystyle y=\frac{1}{3}\times (3)=1\,\)
上限は \(\displaystyle y=\frac{5}{3}\times (3)=5\)
\(\,m=\color{red}{3}\,\)のときこれを満たすのは
\(\,n=\color{blue}{1,2,3,4,5}\,\)
\(\,x=4\,\)のとき、
下限は \(\displaystyle y=\frac{1}{3}\times (4)=\frac{4}{3}\,\)
上限は \(\displaystyle y=-(4)+8=4\)
\(\,m=\color{red}{4}\,\)のときこれを満たすのは
\(\,n=\color{blue}{2,3,4}\,\)
(\(\,n=1\,\)は下限を下回るので不適になります。）
\(\,x=5\,\)のとき、
下限は \(\displaystyle y=\frac{1}{3}\times (5)=\frac{5}{3}\,\)
上限は \(\displaystyle y=-(5)+8=3\)
\(\,m=\color{red}{5}\,\)のときこれを満たすのは
\(\,n=\color{blue}{2,3}\,\)
\(\,x=6\,\)のとき、
下限は \(\displaystyle y=\frac{1}{3}\times (6)=2\,\)
上限は \(\displaystyle y=-(6)+8=2\)
\(\,m=\color{red}{6}\,\)のときこれを満たすのは
\(\,n=\color{blue}{2}\,\)
さいころの出目\(\,36\,\)通りすべて調べました。
\(\,36\,\)通り中\(\,15\,\)通りが\(\,\mathrm{△AOB}\,\)の内部または周上にあります。
\(\displaystyle \frac{15}{36}=\frac{5}{12}\)
（答え）\(\,\displaystyle \underline{ \frac{5}{12} }\,\)
\(\,m=1,2,3,4,5,6\,\)を調べるのですが、
明らかに内部と分かる点は数え上げるだけで、
きわどいところの点と境界となる直線との上限を見れば良いですよ。
ただし、格子点問題では格子点に●をつけていくと分かり易くなるというのは大学入試でも同じです。
以上で\(\,\large{5}-Ⅰ\,\)は終わりです。
⇒ 2018年度秋田県公立高校入試数学の過去問第5問-2の解説
もう一つの選択問題\(\,\large{5}-Ⅱ\,\)では直線だけではなく直線と放物線との間にある格子点です。
しかし、問題としては\(\,\large{5}-Ⅰ\,\)と同じです。
解くのは楽だけど、説明するのは手間がかかるってことが分かってもらえたかな？笑
あれこれ手を出さなくて良いから、徹底的に『覚え太郎』に専念してください。
自信をもっておすすめします。
ほとんどが同じ問題に見えてきますよ。
クラブ活動で忙しい！
塾に通っているのに数学が苦手！
数学の勉強時間を減らしたい！
数学の勉強方法が分からない！
その悩み、『覚え太郎』が解決します！！！
