2018年度秋田県公立高校入試数学の過去問第5問-2の解説

秋田県で2018年(平成30年度)に行われた公立高校入試の数学の第5問-2の解説です。
第5問は学校指定の選択問題になるますが5－1とともに関数と確率の融合です。
関数の基本問題部分は簡単ですが、指定された確率の範囲を出すのに苦労しそうな人は数学の問題への取り組み方を変えた方が良いかもしれません。

問題は秋田県の公式サイトにもあります。

⇒　2018年秋田県公立入試数学過去問

　\(\,\large{5-Ⅱ}\,\)

　『指示された問題について答えなさい。』
と問題にあります。
受験する学校によって指定されますので秋田県の受験生は間違えないようにしましょう。

2つの関数が与えられています。

　ア：\(\displaystyle y=\frac{1}{4}x^2\,\)
　イ：\(\,y=-x+b\,\)
イの直線は切片によって移動します。

(1)
放物線ア上の点\(\,\mathrm{A}\,\)は\(\,x\,\)座標が\(\,3\,\)です。

　\(\displaystyle y=\frac{1}{4}x^2\,\)に\(\,x=3\,\)を代入して

　\(\begin{eqnarray}
y&=&\frac{1}{4}\times (3)^2\\
&=&\frac{9}{4}
\end{eqnarray}\)

これから　\(\displaystyle \mathrm{A\,\left(\,3\,,\,\frac{9}{4}\,\right)}\,\)

直線イが\(\,\mathrm{A}\,\)を通るとき

　\(\,y=-x+b\,\)に\(\displaystyle \mathrm{A\,\left(\,3\,,\,\frac{9}{4}\,\right)}\,\)を代入して成り立つので

　\(\begin{eqnarray}
\left(\frac{9}{4}\right)&=&-(3)+b\\
9&=&-12+4b\\
21&=&4b\\
\frac{21}{4}&=&b
\end{eqnarray}\)

（答え）　\(\displaystyle \underline{　b=\frac{21}{4}　}\,\)

(2)は①②まであり、放物線と格子点の数数えがひかえているのでとっとと終わらせましょう。

大小2つのさいころ1回投げて、

　大きいさいころの出目を\(\,m\,\)
　小さいさいころの出目を\(\,n\,\)
として
　座標\(\,(m,n)\,\)とする。

\(\,\large{5}-Ⅰ\,\)と違うのは\(\,m,n≦6\,\)を意識しなくてはならないないことです。
これは後の問題で説明します。

①\(\,b=\color{red}{6}\,\)のとき、イの直線は\(\,y=-x+\color{red}{6}\,\)です。

点\(\,(m,n)\,\)が\(\,y\,\)軸とアの放物線とイの直線と\(\,x≧0\,\)とで囲まれた範囲にある確率です。
ただし、曲線上の点も含むことになっています。

あえて言う必要はないと思いますが、直線も曲線の一部です。
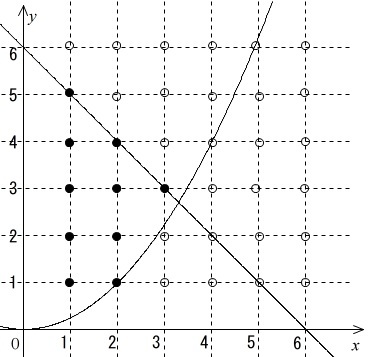●は範囲内にある点です。

この●と○の違いを見つけるのは簡単です。

\(\,x=1,2,3,4,5,6\,\)で
　上限となる\(\,y=-x+6\,\)の座標
と
　下限となる放物線\(\,y=\displaystyle \frac{1}{4}x^2\,\)の座標
を求めておけば良いだけです。

　\(\begin{array} {|c|c|c|c|c|c|c|}\hline
x & 1 & 2 & 3 & 4 & 5 & 6\\ \hline
y=-x+6 & \color{red}{5} & \color{red}{4} & \color{red}{3} & \color{red}{2} & \color{red}{1} & \color{red}{0}\\ \hline
y=\displaystyle \frac{1}{4}x^2 & \color{blue}{\displaystyle\frac{1}{4}} & \color{blue}{1} & \color{blue}{\displaystyle\frac{9}{4}} & \color{blue}{4} & \color{blue}{\displaystyle\frac{25}{4}} & \color{blue}{9}\\ \hline
\end{array}\)

この表を見ながら数えましょう。

　\(\,m=1\,\)のとき下限は\(\,\color{blue}{1}\,\)、上限は\(\,\color{red}{5}\,\)なので
　　\(\,n=1,2,3,4,5\,\)
　\(\,m=2\,\)のとき下限は\(\,\color{blue}{1}\,\)、上限は\(\,\color{red}{4}\,\)なので
　　\(\,n=1,2,3,4\,\)
　\(\,m=3\,\)のとき下限は\(\,\color{blue}{3}\,\)、上限は\(\,\color{red}{3}\,\)なので
　　\(\,n=3\,\)

　\(\,m≧4\,\)では囲まれる点はありません。

座標\(\,(m.n)\,\)の\(\,36\,\)点中範囲内に\(\,10\,\)点あります。

　\(\displaystyle \frac{10}{36}=\frac{5}{18}\)

（答え）\(\displaystyle \underline{　\frac{5}{18}　}\)

ここまでくれば②は簡単です。
\(\,y=-x+b\,\)が平行移動するとき切片が変わります。
条件満たす確率が\(\,\displaystyle \frac{1}{2}\,\)になるということは、
範囲に含まれる点\(\,(m,n)\,\)が\(\,18\,\)点あるということで、
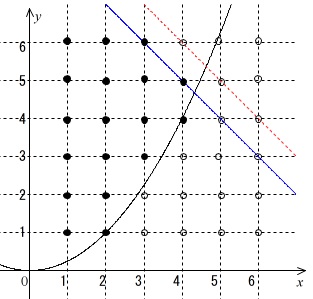傾き考えると青い直線のとき下限で、赤い直線のとき上限で含まれない。
（上限を含むと範囲内の点が増えるので確率が違ってきます。）