平面図形で使う線分,半直線,直線,弧,平行,垂直などの用語と記号

平面図形で使う線分や弧の表し方や、平行と垂直などの基本的な記号の使い方など用語の確認です。
線分と半直線と直線の意味の違いを知らない人も多くいますが、空間も平面と同じあつかいかたをしますので必ず覚えておくようにしましょう。
円と接線との位置関係や平面に垂直な直線の持つ性質も加えて説明しておきます。

線分や半直線の表し方と弧の表し方

用語と記号の確認なので簡単に済ませましょう。

　線分\(\,\mathrm{AB}\,\)は単に\(\,\mathrm{\color{blue}{AB}}\,\)　または　\(\,\mathrm{\color{blue}{\overline{AB}}}\,\)

と表します。
円周上を結ぶ線分の場合は『弦\(\,\mathrm{AB}\,\)』ということもありますが弦も線分の1つです。

　弧\(\,\mathrm{AB}\,\)は線分と区別するために　\(\,\mathrm{ \color{red}{\stackrel{\Large{\frown}}{\mbox{AB}}}}\,\)

と表します。

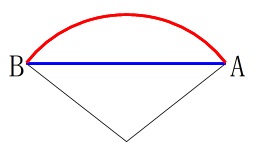
また、線分や弧が等しいとき等号を使って表します。
（線分や弧は「長さ」をつけなくて『等しい』というときは長さを意味します。）

例　\(\mathrm{AB=BC}　,　\mathrm{ \stackrel{\Large{\frown}}{\mbox{AB}}}=\mathrm{ \stackrel{\Large{\frown}}{\mbox{BC}}}\,\)

ところで、線分はよく聞くので知っている人は多いですが、
　『半直線って何？』
という高校も多くいます。

\(\,2\,\)点を結んでできる直線の一部が線分です。

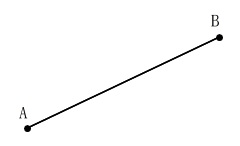
片方に伸びた直線を半直線といいます。
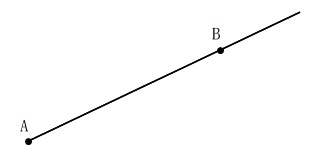呼び方は『半直線\(\,\mathrm{AB}\,\)』です。

半直線\(\,\mathrm{BA}\,\)は始点が逆ですね。

単なる用語なので『覚え太郎』で確認しておいてください。

⇒　中学数学のすべてを短期攻略する『覚え太郎』

直線\(\,\mathrm{AB}\,\)は線分のように限りがあるわけではなく、永遠に伸びているまっすぐな線のことを意味するので忘れないようにしましょう。

平面でも、空間でも同じです。
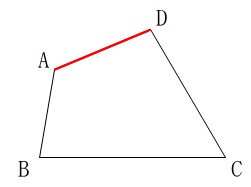『線分\(\,\mathrm{AD}\,\)』と書いてあれば\(\,\mathrm{A,D}\,\)を端点とする長さのある線です。
しかし、直線\(\,\mathrm{AD}\,\)と書かれている場合は、\(\,\mathrm{AD}\,\)の外にもずっとある線のことなので忘れないでください。

直線の意味は、空間図形で再度確認することになります。

平行と垂直の記号

平行は割と単純です。
線分でも直線でも平行は同じ意味です。

　線分\(\,\mathrm{AB}\,\)と線分\(\,\mathrm{EF}\,\)が平行は　\(\,\mathrm{AB\,/\!/\,EF}\,\)

　直線\(\,\mathrm{AB}\,\)と直線\(\,\mathrm{EF}\,\)が平行は　\(\,\mathrm{AB\,/\!/\,EF}\,\)

線分は伸ばすと直線ですが、平行ならずっと先まで平行なので直線でも平行な位置関係は変わりません。

※
平行の記号が　\(\,/\!/\,\)　なのは日本だけとか、考えなくて良いですよ。
高校卒業するまで使ってください。
もしも、\(\,\mathrm{AB\,\parallel\,EF}\,\)となっていても平行を意味します。

垂直の記号も簡単です。

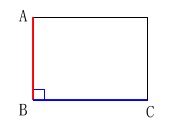
　線分\(\,\mathrm{AB}\,\)と線分\(\,\mathrm{BC}\,\)が垂直なとき　\(\,\mathrm{\color{red}{AB}　⊥　\color{blue}{BC}}\,\)

と表します。

ここでは平面図形に限定して、垂直な（直角に交わる）線分を考えていれば良いので、
　『垂直に交わる線分（直線）\(\,\mathrm{AB　⊥　BC}\,\)』
としておいて良いです。

空間図形ではさらに平面と直線の位置関係を見るようになります。
平面図形だけで垂直を考えると理解しきれないことが出てくるのですが、
ややこしくなるのでここでは垂直という記号だけは覚えておくようにしましょう。

空間図形のときに説明することになるでしょう。
忘れていなければ、ですが。笑

円と接線の関係と用語の確認問題

平面図形で使う記号の基本練習問題を取り上げておきます。

問\(\,1\,\)
右の図の台形\(\,\mathrm{ABCD}\,\)で，点\(\,\mathrm{E，F，G，H}\,\) は,

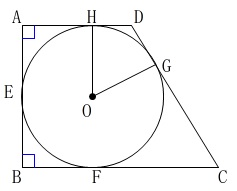
それぞれ辺と円との接点である。次の問いに答えなさい。
　
　\(\,\mathrm{(1)}\,\) 線分\(\,\mathrm{OG}\,\)と線分\(\,\mathrm{OH}\,\)の長さが等しいことを式でしなさい。

　\(\,\mathrm{(2)}\,\) 辺\(\,\mathrm{AD}\,\)と辺\(\,\mathrm{BC}\,\)が平行であることを記号を使って表しなさい。

　\(\,\mathrm{(3)}\,\) 線分\(\,\mathrm{OG}\,\)と\(\,\mathrm{DC}\,\)が垂直であることを記号を使って表しなさい。

(\(\,1\,\))
数学で線分（の長さ）を表すのは、端点２つ(２つの端の点)を並べれば良いだけです。

　端点が\(\,\mathrm{O}\,\)と\(\,\mathrm{G}\,\)を表す線分は\(\,\mathrm{OG}\,\)
　端点が\(\,\mathrm{O}\,\)と\(\,\mathrm{H}\,\)を表す線分は\(\,\mathrm{OH}\,\)

これらが等しいことを表すのは　
　\(\,\mathrm{\underline{　\color{red}{OG=OH}　}}\,\)

とするだけです。
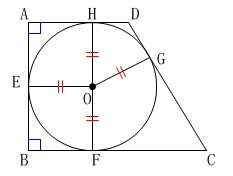円の半径は常に等しいので
　\(\,\mathrm{OE=OF=OG=OH}\,\)
となります。

円とは
　中心から等しい距離にある点の集まり
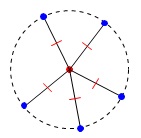です。
このことは問題の中にかくされる条件としてよく使われますので忘れないようにしましょう。
特に、入試の問題では半径が等しい二等辺三角形を見抜けるかを聞いてきます。

ここでは線分（の長さ）が等しいことに
　\(\,\color{red}{(等号)　=}\,\)
を使っていますが、弧の長さが等しいことや面積や体積が等しいことにも使います。
もちろん文章題で使う金額や人数などに使うように、
　『日本語の等しい』を数学では\(\,『\,\large{=}\,』\,\)
で表します。

(\(\,2\,\))
　
次に「平行」という日本語を数学の言葉に代えると、「　\(\,/\!/\,\)　」になります。
　
　答えは、\(\underline{　\color{red}{AB\,/\!/\,BC}　}\)　

(\(\,3\,\))

次に「垂直」は、数学では「　⊥　」という記号を使います。

　答えは、　\(\,\mathrm{\underline{　\color{red}{OG　\perp　DC}　}}\,\)　です。

何故、\(\,\mathrm{OG　\perp　DC}\,\) となるか説明しておきます。

円と接線の位置関係は、

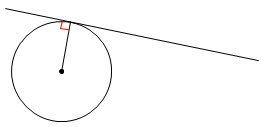
　中心と接線との距離が半径
かつ
　中心と接点を結ぶ半径は接線と垂直
になります。