2019年度神奈川県で行われた公立高校入試の数学問題問3の解説です。
問3は平面図形の問題が2つと1次方程式の立式問題が1つの計3問あります。
平面図形は円と二等辺三角形の組み合わせとややこしそうに見える面積比ですが1本の補助線を引くだけです。
1次方程式は連立方程式と考えても簡単に立式できます。
問題は神奈川県の公式サイトにもあります。
問\(\,3\,\)
（ア）
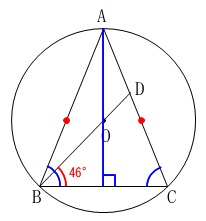
条件を抜き出しておきます。
\(\,3\,\)点\(\,\mathrm{A,B,C}\,\)は円\(\,\mathrm{O}\,\)の周上
\(\,\mathrm{AB=AC}\,\)
点\(\,\mathrm{D}\,\)は\(\,\mathrm{BO}\,\)の延長と\(\,\mathrm{AC}\,\)との交点
\(\,\mathrm{∠DBC=46^{\circ}}\,\)
図を与えてくれています。
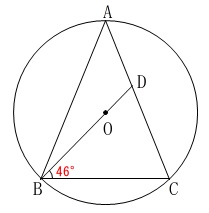方法はいくつもありそうですが、もっともらしい円周角の定理を利用してみます。
\(\,\mathrm{△ABC}\,\)は\(\,\mathrm{AB=AC}\,\)の二等辺三角形ですが、
半径は常に等しいので\(\,\mathrm{△OBC}\,\)も二等辺三角形です。
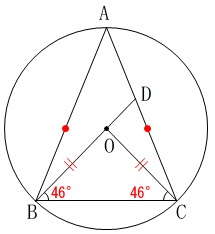
これから\(\,\stackrel{\large{\frown}}{\mbox{BC}}\, \)の中心角は、
\(\begin{eqnarray}
\mathrm{∠BOC}&=&180-46\times 2\\
&=&180-92\\
&=&88 (度)
\end{eqnarray}\)
円周角は中心角の半分なので
\(\,\mathrm{∠BAC=\color{blue}{44}^{\circ}}\,\)
また、\(\,\mathrm{△ABC}\,\)が頂角を\(\,\mathrm{A}\,\)とする二等辺三角形なので
\(\begin{eqnarray}\displaystyle
\mathrm{∠ABC}=\mathrm{∠ACB}&=&\frac{180-44}{2}\\
&=&\frac{136}{2}\\
&=&68 (度)
\end{eqnarray}\)
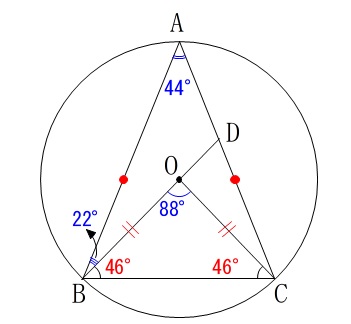
このことから
\(\,\mathrm{∠ABD=66-48=\color{blue}{22} (度)}\,\)
よって
\(\,\mathrm{∠BDC=\color{blue}{44}+\color{blue}{22}=\underline{ 66^{\circ} }}\,\)
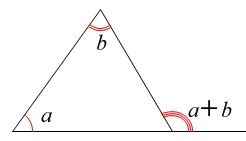三角形の内角の和から\(\,\mathrm{∠ADB}\,\)を出して、
\(\mathrm{∠BDC}=180^{\circ}-\mathrm{∠ADB}\)
と求めても良いです。
この問題解説にあまり時間をかけたくないのですが、
\(\,\mathrm{\color{green}{AB=AC}}\,\)
という条件を先に使うことにすると、
底角か頂角を文字を使って表しても良いですが、
\(\,\mathrm{A,B,C}\,\)が円周上にある。
という条件はどちらにしろ使わなければなりません。
必要無い条件は問題にはありませんよ。
（イ）
『覚え太郎』会員には、
『超え太郎』の相似\(\,\mathrm{No.51}\,\)か\(\,\mathrm{No.64}\,\)のどちらを使えばすぐ終わる。
と簡単に説明は終わるのですが、高校生レベルになるのでここではていねいにやりますよ。笑
条件はもちろん読み取ります。
\(\,\mathrm{D}\,\)は\(\,\mathrm{AB}\,\)の中点
\(\,\mathrm{E,F}\,\)は\(\,\mathrm{AC}\,\)の\(\,3\,\)等分点
\(\,\mathrm{DC}\,\)と\(\,\mathrm{BE}\,\)の交点が\(\,\mathrm{G}\,\)
\(\,\mathrm{DC}\,\)と\(\,\mathrm{BF}\,\)の交点が\(\,\mathrm{H}\,\)
当然図示しますが、1つ補助線を加えておきましょう。
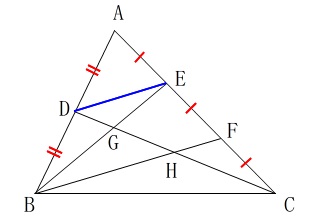
補助線が必要なときは垂線か平行線だと考えて良いです。
もちろん中心と円周上の点を結ぶとか、離れた\(\,2\,\)点があれば結ぶのは普通ですが、ポイントになる補助線はほとんどが平行線か垂線です。
この問題では平行線と考えなくても平行になります。
等分した点と点といえば中点連結定理でしょう。
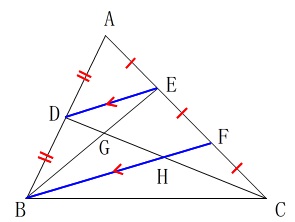先に\(\,\mathrm{△ABF}\,\)と\(\,\mathrm{△ADE}\,\)に着目します。
点\(\,\mathrm{\color{red}{D,E}}\,\)は\(\,\mathrm{AB,AF}\,\)の中点になるので中点連結定理から
\(\mathrm{\color{blue}{DE}}\,\)∥\(\,\mathrm{\color{red}{BF}}\,\)
\(\displaystyle \mathrm{\color{blue}{DE}=\frac{1}{2}\color{red}{BF}} ⇔ \mathrm{\color{red}{BF}=2\color{blue}{DE}} ･･･☆\)
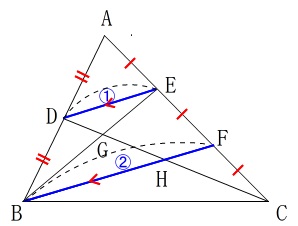
今度は
\(\,\mathrm{\color{blue}{DE}}\,\)∥\(\,\mathrm{\color{red}{BF}}\,\)
から
\(\,\mathrm{△CDE}\,\) ∽ \(\,\mathrm{△CHF}\,\)
に着目して、
\(\,\mathrm{CF=FE}\,\) なので \(\,\mathrm{CH=HD}\,\)
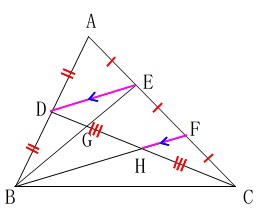中点連結定理から、（相似比でも同じ）
\(\,\mathrm{\color{blue}{DE}}\,\)∥\(\,\mathrm{\color{magenta}{HF}}\,\)
\(\,\mathrm{\color{blue}{DE}=2\color{magenta}{HF}}\,\)
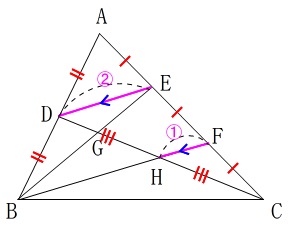\(\,\mathrm{\color{magenta}{HF}}\,\)を①とすると
\(\,\mathrm{\color{blue}{DE}=2\color{magenta}{HF}}\,\) から \(\,\mathrm{\color{blue}{DE}=\color{red}{②}}\,\)
\(\,\mathrm{☆}\,\)の関係から
\(\,\mathrm{\color{red}{BF}=2\color{blue}{DE}}\,\) なので \(\,\mathrm{\color{red}{BF}=4\color{magenta}{HF}=\color{red}{④}}\,\)
\(\,\mathrm{BH:HF=\color{red}{③}:\color{red}{①}}\,\)の説明はいらないでしょう。
ちょっと疑問に思うことがあります。
私は何故この程度のことに図をいっぱい書いて、時間を費やしているんだろう？笑
基本が大事と言うことです。
後は面積比ですが、分かる人と分からない人の大きな差となるところなのでさっと済ませます。
これが分からないという人は基本作業からやり直しておきましょう。
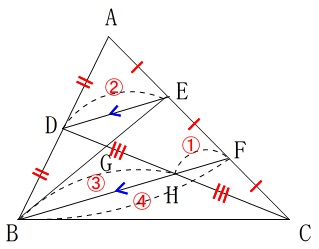
\(\,\mathrm{DE}\,\) ∥ \(\,\mathrm{BH}\,\)
なので錯角は等しいことから
\(\,\mathrm{△GDE}\,\) ∽ \(\,\mathrm{△GHB}\,\)
相似比は②:③だから
\(\,\mathrm{DG：GH=2:3}\,\)
また\(\,\mathrm{CH=HD=HG+GD}\,\)なので
\(\,\mathrm{\color{blue}{DG:GH:CH}=\color{blue}{2:3:5}}\,\)
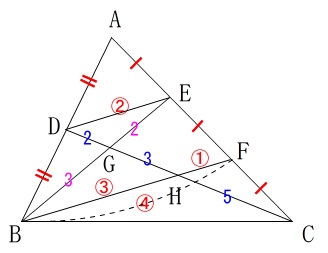同じ色の数字は対応する線分比と見てください。
何故こんなことをやっているかというと、この図形には三角形は辺の長さが1つもありません。
ということは具体的な面積を求めて比を出す問題では無いということです。
つまり、
『線分比から面積比を出しなさい。』
という問題だから線分比を分かるだけ出していこうという方針です。
ここまでですべての線分比を出しましたので後は圧縮すれば終わりです。
長い説明ですけど、中点連結定理と相似しか使っていません。
問題なのは四角形\(\,\mathrm{EGHF}\,\)の面積でしょうけど、いくらでも方法はあります。
四角形の面積を求める方法は、公式が使える四角形以外は、
三角形2つを足す
か
三角形から三角形を引く
のどちらかになります。
四角形に限らず、公式のない面積を求めるときは
『部分』＋『部分』
『全体（部分）』－『部分』
です。
この『部分』や『全体』は公式がある図形です。
面積比を整数比で出す場合、線分の比がいろいろ出てきますが、
すべての線分比として出てくる数の公倍数
で基準の面積をおくとやりやすいのですが、ここでは２つの線分比を取らなくてはならないので気づきにくいでしょうから、
すべての問題で通用するようにやっておきます。
\(\,\mathrm{△ABC}\,\)の面積を\(\,1\,\)とします。
底辺を\(\,\mathrm{AB}\,\)としたとき
\(\,\mathrm{AD:DB=1:1}\,\)
で高さは共通しているので、
\(\begin{eqnarray}\displaystyle
\mathrm{△CBD}&=&\frac{1}{2}\times \mathrm{△ABC}\\
&=&\color{blue}{\frac{1}{2}}
\end{eqnarray}\)
さらに
\(\,\mathrm{DG:CG=2:8=1:4}\,\)
なので
\(\begin{eqnarray}\displaystyle
\mathrm{\color{red}{△BGD}}&=&\frac{1}{5}\times \mathrm{△CBD}\\
&=&\frac{1}{5}\times \color{blue}{\frac{1}{2}}\\
&=&\color{red}{\frac{1}{10}} ･･･ \mathrm{\color{red}{S}}
\end{eqnarray}\)
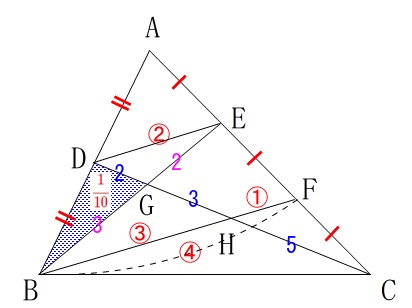次に\(\,\mathrm{△ABC}\,\)に対する四角形\(\,\mathrm{EGHF}\,\)の面積比です。
この四角形は公式では求まりませんので、
『部分』－『部分』
を利用しましょう。
いろいろな見方があるのでいろいろな方向に行けますが、
\(\,\mathrm{四角形EGHF=△BEF-△BGH}\,\)
と見ます。
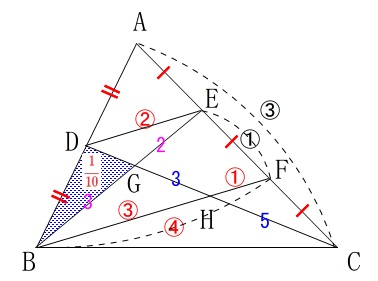\(\,\mathrm{E,F}\,\)は\(\,\mathrm{AC}\,\)を\(\,3\,\)等分しているので、
\(\begin{eqnarray}\displaystyle
\mathrm{\color{blue}{△BEF}}&=&\frac{1}{3}\times \mathrm{△ABC}\\
&=&\color{blue}{\frac{1}{3}}
\end{eqnarray}\)
また\(\,\mathrm{DG:GH:HC=2:3:5}\,\)なので\(\,\mathrm{△BGH}\,\)は
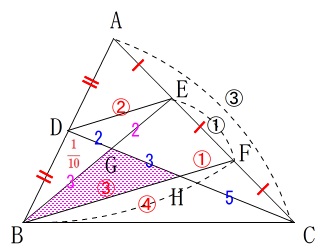
\(\begin{eqnarray}\displaystyle
\mathrm{\color{magenta}{△BGH}}&=&\frac{3}{2+3+5}\times \mathrm{\color{red}{△CBD}}\\
&=&\frac{3}{10}\times \color{red}{\frac{1}{2}}\\
&=&\color{magenta}{\frac{3}{20}}
\end{eqnarray}\)
部分を引くと
\(\begin{eqnarray}\displaystyle
\color{red}{四角形\mathrm{EGHF}}&=&\mathrm{\color{blue}{△BEF}-\color{magenta}{△BGH}}\\
&=&\color{blue}{\frac{1}{3}}-\color{magenta}{\frac{3}{20}}\\
&=&\frac{20-3\times 3}{60}\\
&=&\color{red}{\frac{11}{60}} ･･･ \mathrm{\color{red}{T}}
\end{eqnarray}\)
よって
\(\begin{eqnarray}\displaystyle
\mathrm{S:T}&=&\frac{1}{10}:\frac{11}{60}\\
&=&\frac{6}{60}:\frac{11}{60}\\
&=&\underline{ 6:11 }
\end{eqnarray}\)
『覚え太郎』会員はこの解説通りではなく、
\(\begin{eqnarray}\displaystyle
\mathrm{△BGH}&=&\frac{1}{3}\times \frac{3}{5}\times \frac{3}{4}\\
&=&\frac{3}{20}
\end{eqnarray}\)
とやった方がはやいですよ。
それほど計算が楽というわけではありませんが、相似から線分比が出た時点で出せるでしょう？
\(\,\mathrm{△ADC}\,\)側で圧縮することもできます。
この面積の比を比べる問題はよく出ますので自分で練習してみると良いですね。
ちなみにですが、
\(\,\mathrm{△ABC}\,\)の面積を\(\,60\,\)の倍数として設定すると整数のままで面積比が出せます。
底辺と見なす辺の比に\(\,2:3:5\,\)と\(\,1:2\,\)の線分比があるからです。
しかし、無視しておいて良いです。
面積が具体的にない場合は、基準の面積を\(\,1\,\)としてあつかえばすべての問題で使えるので\(\,1\,\)で通しておきましょう。
（ウ）
方程式の立式では何が変化してないか、
何が等しいのかを＝で結べば良いだけです。
与えられた条件は
\(\,6\,\)個ずつ分けると\(\,8\,\)個足りない。
\(\,5\,\)個ずつ分けると\(\,5\,\)個余る。
分かっていないのは「人数」と「みかんの個数」です。
変化していない（等しい）のも「人数」と「みかんの個数」です。
この問題ではみかんの個数を\(\,x\,\)としておいて立式するように指示があります。
\(\,x\,\)個のみかんを\(\,6\,\)個ずつ分けると\(\,8\,\)個足りない。
このときの人数は、みかんを\(\,8\,\)個足せば割り切れて
\(\displaystyle \frac{x+8}{6}\)
\(\,5\,\)個ずつ分けると\(\,5\,\)個余る。
このときの人数は、逆に\(\,5\,\)個引けば割り切れて
\(\displaystyle \frac{x-5}{5}\)
この2つの人数は変化していないので
\(\displaystyle \underline{ \frac{x+8}{6}= \frac{x-5}{5} } ･･･ (ⅰ)\)
これを解いて
\(\begin{eqnarray}\displaystyle
\frac{x+8}{6}&=&\frac{x-5}{5}\\
5(x+8)&=&6(x-5)\\
5x+40&=&6x-30\\
5x-6x&=&-30-40\\
-x&=&-70\\
x&=&\underline{ 70 } (個)･･･ (ⅱ)
\end{eqnarray}\)
この問題は\(\,x\,\)で立式するように指定しているので難しく感じたかもしれませんが、
ふつうならみかんの個数\(\,x\,\)、人数\(\,y\,\)とおいて連立方程式にしませんか？
（みかんの個数を\(\,x\,\)とするのは問題にしたがっています。）
このとき
\(\,6\,\)個ずつ分けると\(\,8\,\)個足りない。
\(\,5\,\)個ずつ分けると\(\,5\,\)個余る。
この2つの条件は割り算の基本定理から
\( \begin{cases}
\hspace{7pt} x=6y-8\\ \\
\hspace{7pt} x=5y+5
\end{cases}\)
ここで\(\,x\,\)を消去してしまうと問題の答えにならないので、\(\,y\,\)について整理すると、
\( \begin{cases}
\hspace{7pt}\displaystyle y=\frac{x+8}{6}\\ \\
\hspace{7pt} \displaystyle y=\frac{x-5}{5}
\end{cases}\)
から聞かれている\(\,x\,\)の方程式
\(\displaystyle \frac{x+8}{6}=\frac{x-5}{5}\)
が出てきます。
答えだけなら、連立方程式を解くだけで出てきますが(ⅰ)を立式できるかどうかですね。
問\(\,3\,\)はこの\(\,3\,\)問ですが、問\(\,7\,\)まであります。
⇒ 2019年度神奈川県公立高校入試の数学問4関数問題の解説
問\(\,4\,\)は関数総合問題です。
与えられたグラフを見た瞬間、ものすごくややこしそうに見えますが、関数でやることは決まっています。
⇒ 2019年度神奈川県公立高校入試の数学問題問1,2の解説
全体の基本問題を解いて、それから応用と感じる問題にチャレンジする方が得点は安定するでしょう。
もちろん、『覚え太郎』にじっくり取り組んだあなたなら、満点狙えます。
クラブ活動で忙しい！
塾に通っているのに数学が苦手！
数学の勉強時間を減らしたい！
数学の勉強方法が分からない！
その悩み、『覚え太郎』が解決します！！！
