2019年度神奈川県公立高校入試の数学問4関数問題の解説

2019年度神奈川県で行われた公立高校入試の数学問題問4の解説です。
問4は関数総合問題ですが、与えられたグラフの見た目ほどややこしくはありません。
基本方針通りで十分解けます。
最後の座標決定問題は解法が分かれると思われますが、標準的な方法で解説しておきます。

問題は神奈川県の公式サイトにもあります。

⇒　2019年度神奈川県立高校入試数学問題

問\(\,4\,\)

（ア）
問題の最初のページに、
　『計算は、問題冊子のあいているところを使いなさい。』
と書いてあります。
この問題ページにはあいているところが少ないですが、問題冊子の最後の数ページは白紙です。
（実際に受けたわけではないので分かりませんが、ここは計算スペースではないでしょうか。）

条件が多いように見えますので書き出して整理しておきましょう。

　直線①は\(\,y=-x\,\)
　曲線②は\(\,y=\frac{1}{3}x^2\,\)
　曲線③は\(\,y=ax^2\,\)
　\(\,\mathrm{A}\,\)の\(\,x\,\)座標は\(\,-3\,\)
　\(\,\mathrm{AB}\,\)は\(\,x\,\)軸に平行
　\(\,\mathrm{AC}\,\)は\(\,y\,\)軸に平行
　\(\,\mathrm{C}\,\)の\(\,y\,\)座標は\(\,-2\,\)
　\(\,\mathrm{AD:DC=2:1}\,\)
　\(\,\mathrm{E}\,\)は\(\,y\,\)軸上の点
　\(\,\mathrm{F}\,\)は\(\,y\,\)軸上で\(\,\mathrm{\color{red}{AD=EF}}\,\)で\(\,y\,\)座標は正

多いですね。
ただ、これを文章で見ていては問題は解けません。

グラフに書き込んで行きましょう。
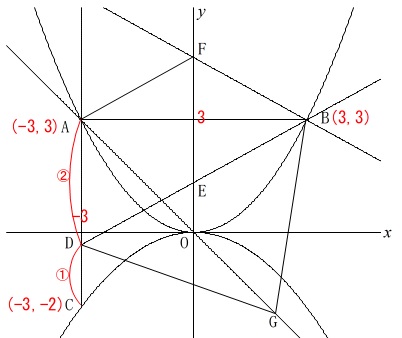グラフは問題に与えられたものを使わないと手書きではきびしいでしょう。
ただし、高校ではすべて手書きになるので入試が終わったら練習しておいても良いかもしれませんね。

\(\,\mathrm{D}\,\)の座標を出しておきたいので計算します。

点\(\,\mathrm{A,D,C}\,\)は\(\,y\,\)軸に平行な直線上の点なので\(\,x\,\)座標が同じです。

点\(\,\mathrm{A}\,\)と\(\,\mathrm{C}\,\)の\(\,y\,\)座標の差は\(\,5\,\)なので、

　\(\,\mathrm{AD:DC=2:1}\,\)

であることから

　\(\displaystyle \mathrm{AD=5\times \frac{2}{3}=\frac{10}{3}}\,\)

　\(\displaystyle \mathrm{DC=5\times \frac{1}{3}=\frac{5}{3}}\,\)

どちらを使っても同じ結果が出ますが、\(\,x\,\)座標は変わらず

　\(\displaystyle \mathrm{\color{blue}{D\,\left(\,-3\,,\,-\frac{1}{3}\,\right)}}\,\)
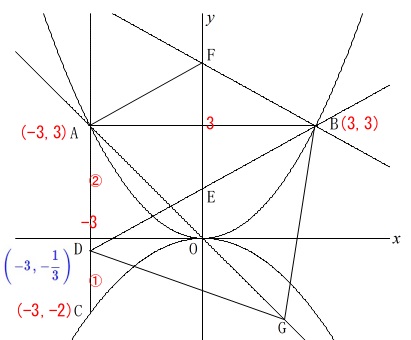（ア）の答えを出すには必要ないですが、\(\,\mathrm{F}\,\)の座標も出しておきましょう。

　\(\,\mathrm{F}\,\)は\(\,y\,\)軸上で\(\,\mathrm{\color{red}{AD=EF}}\,\)で\(\,y\,\)座標は正

\(\,\mathrm{E}\,\)は直線\(\,\mathrm{DB}\,\)の切片なので直線\(\,\mathrm{DB}\,\)の方程式を求めます。
点\(\,\mathrm{B}\,\)は放物線上の点で\(\,y\,\)座標が同じなので\(\,y\,\)軸を軸として\(\,\mathrm{A}\,\)の対称な点になります。

　\(\displaystyle \mathrm{D}\,\left(\,-3\,,\,-\frac{1}{3}\,\right)\,\)
　\(\mathrm{B}\hspace{6pt}(\hspace{10pt}3\,,\hspace{10pt}3\hspace{6pt})\,\)
の\(\,2\,\)点を通る直線です。

　\(\,xの増加量=3-(-3)=\color{red}{6}\,\)
　\(\displaystyle \,yの増加量=3-\left(-\frac{1}{3}\right)=\color{blue}{\frac{10}{3}}\,\)

なので直線\(\,\mathrm{DB}\,\)の傾きは

　\(\hspace{10pt}\displaystyle \frac{\color{blue}{\frac{10}{3}}}{\color{red}{6}}=\frac{10}{3}\times \frac{1}{6}=\frac{5}{9}\)

切片を\(\,b\,\)とおくと
　\(\displaystyle y=\frac{5}{9}x+b\,\)

点\(\,\mathrm{D,B}\,\)のどちらも通るのでどちらかを代入すると、\(\,b\,\)が決まります。
ここでは\(\,\mathrm{B(\,3\,,\,3\,)}\,\)を代入します。

　\(\begin{eqnarray}\displaystyle
3&=&\frac{5}{9}\times (3)+b\\
3&=&\frac{5}{3}+b\\
9&=&5+3b\\
3b+5&=&9\\
3b&=&9-5\\
3b&=&4\\
b&=&\frac{4}{3}
\end{eqnarray}\)

直線\(\,\mathrm{DB}\,\)の方程式は
　\(\displaystyle y=\frac{5}{9}x+\frac{4}{3}\)

点\(\,\mathrm{E}\,\)の座標は
　\(\displaystyle\color{blue}{ \mathrm{E}\,\left(\,0\,,\,\frac{4}{3}\,\right)}\,\)

\(\,\mathrm{AD=EF}\,\)なので
\(\,\mathrm{F}\,\)の座標は\(\,y\,\)座標が\(\,\mathrm{E}\,\)より\(\displaystyle \,\frac{10}{3}\,\)増え、

　\(\displaystyle\color{blue}{ \mathrm{F}\,\left(\,0\,,\,\frac{14}{3}\,\right)}\,\)　
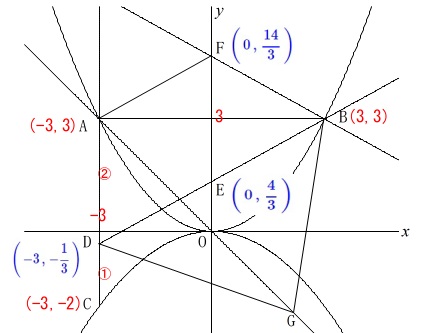もう一度言っておきます。

（ア）を答えるだけなら必要無いことをやっています。
しかし、関数で満点とりたいというときやらなければならないことを先にやっているだけです。

問題によっては必要無いこともありますが、すべての交点とすべての直線を出しておけばほとんどの問題は解決しています。
誘導がないからやらない人が多いだけです。

他にももっと分かることはありますが、伝えたいことは伝えたので（ア）を答えましょう。

曲線③は点\(\,\mathrm{C}\,\)を通ります。

　\(\,\mathrm{C}\,\)の\(\,y\,\)座標は\(\,-2\,\)

からすでに\(\,\mathrm{C}\,\)は\(\,(\,-3\,,\,-2\,)\,\)と求めているので説明は飛ばします。

　\(\,y=ax^2\,\)が\(\,(\,-3\,,\,-2\,)\,\)を通ることから

　\(\begin{eqnarray}\displaystyle
(-2)&=&a\times (-3)^2\\
-2&=&9a\\
a&=&\underline{　-\frac{2}{9}　}
\end{eqnarray}\)

（イ）
直線\(\,\mathrm{BF}\,\)の方程式\(\,y=mx+n\,\)を求めて、
傾きと切片を解答の選択肢から選べば良いだけです。

　\(\,\mathrm{B\hspace{6pt}(\,3\,,\hspace{6pt}3\hspace{6pt})}\,\)
　\(\displaystyle \,\mathrm{F\,\left(\,0\,,\,\frac{14}{3}\,\right)}\,\)

連立方程式でも良いですが、傾きから出します。

\(\,1\,\)次関数の傾きは変化の割合に一致しますので

　\( \,\color{red}{\,(\,x\,の増加量\,)\,}=0-(3)=\color{red}{-3}\,\)
　\(\displaystyle\,\color{blue}{\,(\,y\,の増加量\,)\,}=\frac{14}{3}-3=\color{blue}{\frac{5}{3}}\,\)

　\(\begin{eqnarray}\displaystyle
m&=&\frac{\color{blue}{\frac{5}{3}}}{\color{red}{-3}}\\
&=&-\frac{5}{3}\times \frac{1}{3}\\
&=&\underline{　-\frac{5}{9}　}
\end{eqnarray}\)

傾きが決まったので
　\(\displaystyle \,y=-\frac{5}{9}x+n\,\)
に\(\,\mathrm{B,F}\,\)のどちらかを代入します。

どっちでも良いですが、
　\(\,\mathrm{B\hspace{6pt}(\,3\,,\hspace{6pt}3\hspace{6pt})}\,\)
を代入します。

　\(\begin{eqnarray}\displaystyle
(3)&=&-\frac{5}{9}\times (3)+n\\
3&=&-\frac{5}{3}+n\\
9&=&-5+3n\\
3n-5&=&9\\
3n&=&9+5\\
n&=&\underline{　\frac{14}{3}　}
\end{eqnarray}\)

ここまでは基本問題なので素早く解いておくと良いです。
先に求めておこうとする直線が多い場合は、この後に必要な直線を求めていくといいです。

（ウ）
これは方針がいくつも立つので迷うかもしれません。

その前に、取り組めない人も多いでしょうけど。
『覚え太郎』で基礎を作り上げていないからですよ。笑

どことどこが等しくなるのか見ておきましょう。

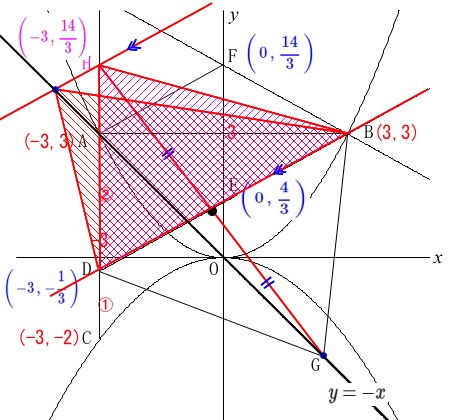
　\(\,\mathrm{\color{red}{△BDG}}\,\)と\(\,\mathrm{\color{blue}{四角形ADBF}}\,\)が等しくなるときです。
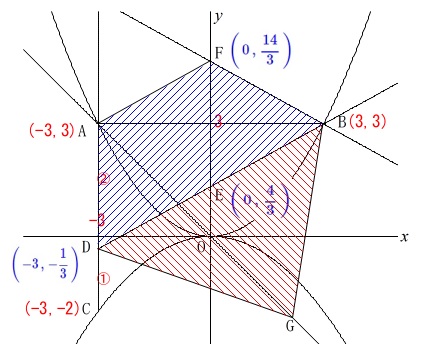四角形\(\,\mathrm{ADBF}\,\)の面積は具体的に簡単に求まります。

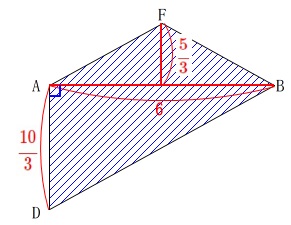
　\(\hspace{10pt}\displaystyle \frac{1}{2}\times 6\times \left(\frac{5}{3}+\frac{10}{3}\right)\\
\displaystyle =3\times\frac{15}{3}\\
=15\)　

しかし、この問題が受験生に求めているのはこの方法ではないのではないでしょうか。
この面積を使う方法を後で示しますが、『超え太郎』マスター向きになります。

いずれにしても、求めるのが直線\(\,y=-x\,\)上の\(\,\mathrm{G}\,\)の座標なので

　\(\,\mathrm{G}\,(\,t\,,\,-t\,)\,\)

と文字でおくことは同じで良いでしょう。

さて、\(\,\mathrm{△BDG}\,\)の面積が\(\,15\,\)となるように定めるには普通の公式では出てきません。

そこで四角形\(\,\mathrm{ADBF}\,\)と等しい面積を表す図形を探してみると、
\(\,\mathrm{F}\,\)を\(\,x=-3\,\)という直線上に\(\,x\,\)軸と平行に移動させた点\(\,\mathrm{H}\,\)を考えます。
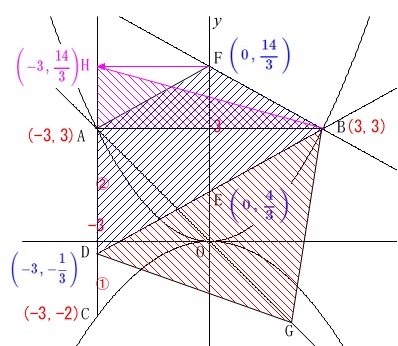すると、
　\(\,\mathrm{△FAB=△HAB}\,\)
なので
　四角形\(\,\mathrm{ADBF}=\mathrm{△HDB}\,\)
となります。

この\(\,\mathrm{△HDB}\,\)と\(\,\mathrm{△BDG}\,\)の面積が等しくなるように\(\,\mathrm{G}\,\)を定めれば良いだけです。

底辺を\(\,\mathrm{DB}\,\)と見て、高さが等しくなれば良いのですが垂直な線分はありません。
しかし、\(\,\mathrm{G}\,\)の\(\,x\,\)座標を正の範囲だけ見れば良いので
　\(\,\mathrm{HG}\,\)と\(\,\mathrm{DB}\,\)の交点が\(\,\mathrm{HG}\,\)の中点
になれば高さは等しくなります。
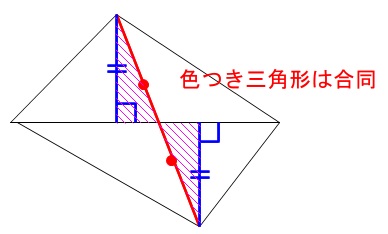逆に見れば、
　\(\,\mathrm{HG}\,\)の中点が直線\(\,\mathrm{DB}\,\)上
にあれば2つの三角形の面積を等しくします。

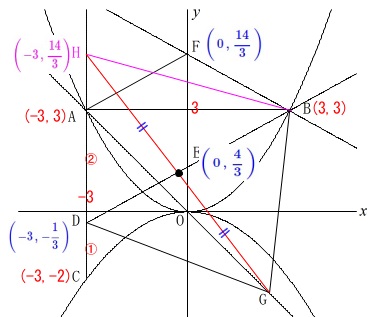\(\,\mathrm{HG}\,\)の中点の座標は\(\,\mathrm{G}\,(\,t\,,\,-t\,)\,\)とおくと

　\(\mathrm{H}\displaystyle \left(\,-3\,,\,\frac{14}{3}\,\right)\)
　\(\mathrm{G}\,(\hspace{6pt}t\hspace{6pt},\,-t\hspace{6pt})\)

の中点なので
　\(\hspace{10pt}\displaystyle \left(\frac{-3+t}{2}\,,\,\frac{\frac{14}{3}+(-t)}{2}\right)\\
\displaystyle =\left(\frac{-3+t}{2}\,,\,\frac{14-3t}{6}\right)\)

これが直線\(\,\mathrm{DB}\,\)上にあるとき面積は等しくなるので
直線\(\,\mathrm{DB}\,\)の方程式
　\(\displaystyle y=\frac{5}{9}x+\frac{4}{3}\)
に代入します。

　\(\begin{eqnarray}\displaystyle
\frac{14-3t}{6}&=&\frac{5}{9}\times \left(\frac{-3+t}{2}\right)+\frac{4}{3}\\
3(14-3t)&=&5(-3+t)+6\times 4\\
42-9t&=&-15+5t+24\\
-9t-5t&=&-15+24-42\\
-14t&=&-33\\
t&=&\underline{　\frac{33}{14}　}
\end{eqnarray}\)

この\(\,t\,\)が求める\(\,\mathrm{G}\,\)の\(\,x\,\)座標です。

問\(\,4\,\)は説明は長いけどこれだけです。

さて、いらないんだけどマスター向けに面積15を利用してみましょう。

\(\,3\,\)点\(\,\mathrm{D,G,B}\,\)は
　\(\mathrm{D}\,\displaystyle \left(\,-3\,,\,-\frac{1}{3}\,\right)\)
　\(\mathrm{G}\,\,(\,t\,,\,-t\,)\,\)
　\(\mathrm{B}\,\,(\,3\,,\,3\,)\,\)

このとき\(\,\mathrm{△BDG}\,\)の面積はすべての点を
　\(\displaystyle \left(\,+3\,,\,+\frac{1}{3}\,\right)\)
だけ平行移動して

　\(\mathrm{D’}\,(\,0\,,\,0\,)\)
　\(\mathrm{G’}\displaystyle \,\left(\,\color{red}{t+3}\,,\,\color{blue}{-t+\frac{1}{3}}\,\right)\,\)　
　\(\mathrm{B’}\displaystyle \left(\hspace{10pt}\color{blue}{6}\hspace{10pt},\hspace{10pt}\color{red}{\frac{10}{3}}\hspace{10pt}\right)\)

で作られる\(\,\mathrm{△D’B’G’}\,\)の面積と変わらないので

　\(\begin{eqnarray}\displaystyle
\mathrm{△BGD}&=&\mathrm{△D’B’G’}\\
&=&\frac{1}{2}\left|\color{red}{(t+3)}\times \left(\color{red}{\frac{10}{3}}\right)-\left(\color{blue}{-t+\frac{1}{3}}\right)\times (\color{blue}{6})\right|\\
&=&\frac{1}{2}\left|\frac{28t+24}{3}\right|
\end{eqnarray}\)

これが四角形\(\,\mathrm{ADBF}\,\)の面積\(\,15\,\)に等しいとき

　\(\begin{eqnarray}\displaystyle
\frac{1}{2}\left|\frac{28t+24}{3}\right|&=&15\\
|28t+24|&=&90\\
t&=&\underline{　\frac{33}{14}　}\,,\,-\frac{57}{14}
\end{eqnarray}\)

\(\,t\,\)は正なので\(\displaystyle \,t=-\frac{57}{14}\,\)は不適です。
この\(\displaystyle \,t=-\frac{57}{14}\,\)は
　\(\,y=-x\,\)上のもう一つの点です。