2019年度神奈川県で行われた公立高校入試の数学問題問1,問2の解説です。
問1と問2は小問集合となっているので、まとめて解説します。
ひねった問題がありませんので確実に取っておきたい問題であり、全体で問題数が多いので手早く処理したいところです。
問題は神奈川県の公式サイトにもあります。
問\(\,1\,\)
（ア）
暗算でもできる問題ですが、基本通り処理しましょう。
\(\hspace{10pt}(-7)+(-13)\\
=-7-13\\
=\underline{ -20 }\)
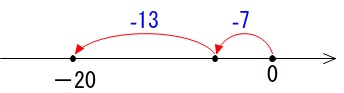
これを
\(\hspace{10pt}-7-13\\
=\color{red}{-(7+13)}\\
=-20\)
とまでする必要はありません。
（イ）
会員には当たり前のことだけど一般の人向けに書いておくと、
文字式であろうが単なる数値計算であろうが、分母は1つにした方が楽ですよ。
分子の計算に集中できますからね。
\(\hspace{10pt}\displaystyle -\frac{3}{5}+\frac{3}{7}\\
\displaystyle =\frac{-3\times 7+3\times 5}{35}\\
\displaystyle =\frac{-21+15}{35}\\
\displaystyle =\frac{-6}{35}=\underline{ -\frac{6}{35} }\)
（ウ）
これも暗算でもできる程度の計算ですが、基本通り処理します。
もちろん、割り算部分を逆数のかけ算にして約分です。
符号がマイナスであることは分かるので前に出しておけば良いですね。
\(\hspace{10pt} 32ab^2\div (-4b)\\
\displaystyle =-\frac{32ab^2}{4b}\\
\displaystyle =\underline{ -8ab }\)
こういった基本的な作業をやっていないと、この程度の計算はできるけど少し応用されるとできない、難しいという状態になります。
どれほどかけ算割り算が増えようと全部同じ処理で良いですよ。
『覚え太郎』会員は『約分の効用』や『基本レポート』で確認してください。
高校で数学を苦手にしたくないなら基本をきっちり身につけておくようにしましょう。
（エ）
素因数分解が先でも有理化が先でも良いですが、一つひとつは確実に処理し、暗算は二段階以上しないようにしましょう。
単純な計算ミスで\(\,-3\,\)点です。
素因数分解は
\(3\,\underline{)\,63}\\
3\,\underline{)\,21}\\
\hspace{17pt}7\)
有理化は
\(\displaystyle \hspace{10pt}\frac{42}{\sqrt{7}}\\
\displaystyle =\frac{42\times \sqrt{7}}{\sqrt{7}\times \sqrt{7}}\\
\displaystyle =\frac{42\sqrt{7}}{7}\\
=6\sqrt{7}\)
よって
\(\hspace{10pt}\displaystyle \sqrt{63}+\frac{42}{\sqrt{7}}\\
=3\sqrt{7}+6\sqrt{7}\\
=\underline{ 9\sqrt{7} }\)
（オ）
算数でも数学でも計算順序は同じ（かっこ）の中が先です。
（かっこ）の中の計算と（かっこ）を外すという処理を同時にしない方が良いですね。
二段階の暗算をすることになり、ミスの原因になりますよ。
\(\hspace{10pt} (x+4)^2-(x-5)(x-4)\\
=(x^2+8x+16)-(x^2-9x+20)\\
=x^2+8x+16\color{red}{-}x^2\color{red}{+}9x\color{red}{-}20\\
=\underline{ 17x-4 }\)
展開公式を使わずに見直しをすれば良い検算になります。
\(\hspace{10pt} (x+4)^2-(x-5)(x-4)\\
=(x+4)(x+4)-(x-5)(x-4)\\
=x^2+4x+4x+16-(x^2-4x-5x+20)\\
=x^2+8x+16-(x^2-9x+20)\\
=x^2+8x+16-x^2+9x-20\\
=\underline{ 17x-4 }\)
問\(\,2\,\)
（ア）
置換すると展開の手間が省ける因数分解です。
\(\,x-4\,\)が同じなので\(\,x-4=\mathrm{A}\,\)と置きましょう。
\(\hspace{10pt}(x-4)^2+8(x-4)-33\\
=\mathrm{A}^2+8\mathrm{A}-33\)
\(\,33\,\)になる因数の組み合わせは
\(\color{black}{\fbox{\(\,1\times 33\,\)}}\) \(\color{red}{\fbox{\(\,3\times 11\,\)}}\)
だけなので分かり易いですね。
\(\hspace{10pt}\mathrm{A}^2+8\mathrm{A}-33\\
=(\mathrm{A}-3)(\mathrm{A}+11)\)
\(\,\mathrm{\color{red}{A}}=\color{red}{x-4}\,\)なので
\(\hspace{10pt}(\mathrm{\color{red}{A}}-3)(\mathrm{\color{red}{A}}+11)\\
=(\color{red}{x-4}-3)(\color{red}{x-4}+11)\\
=\underline{ (x-7)(x+7) }\)
選択する答えは因数の順序が逆ですが同じものです。
これを展開してから因数分解しても良いですが、満点狙うなら時間を考えておきましょう。
\(\hspace{10pt}(x-4)^2+8(x-4)-33\\
=x^2-8x\color{red}{+16}+8x\color{red}{-32-33}\\
=x^2-49\\
=\underline{ (x+7)(x-7) }\)
\(\,7\,\)割狙いの人は展開して進めて良いですが、定数項はきっちり筆算しておいた方が良いですよ。
（イ）
「方程式の解を求める」ことと「方程式を解く」ことは同じことです。
\(\,2\,\)次方程式の場合は因数分解できないか、を先ず検討しますが、
ここでは2次の係数が\(\,1\,\)ではないし、共通因数もないので因数分解できそうもありません。
迷うくらいななら解の公式で突っ走っていいです。
\(\,3x^2-8x+2=0\,\)
解の公式を利用して
\(\begin{eqnarray}\displaystyle
x&=&\frac{-8\pm \sqrt{(-8)^2-4\times (3)\times (2)}}{2\times (3)}\\
&=&\frac{-8\pm \sqrt{64-24}}{6}\\
&=&\frac{-8\pm \sqrt{40}}{6}\\
&=&\frac{-8\pm 2\sqrt{10}}{6}\\
&=&\underline{ \frac{-4\pm \sqrt{10}}{3} }
\end{eqnarray}\)
部分的に約分しないようにしましょう。
\(\displaystyle \frac{-\color{red}{8}\pm \color{red}{3}\sqrt{10}}{\color{red}{6}}\)
のような場合は約分はできません。
※
この\(\,2\,\)次方程式は\(\,x\,\)の\(\,1\,\)次の項の係数が偶数なので、
\(\begin{eqnarray}\displaystyle
x&=&\frac{-4\pm \sqrt{(-4)^2-(3)\times (2)}}{3}\\
&=&\frac{-4\pm \sqrt{16-6}}{3}\\
&=&\frac{-4\pm \sqrt{10}}{3}
\end{eqnarray}\)
とできますが中学生は無理しなくて良いです。
解の公式を利用せず
\(\begin{eqnarray}\displaystyle
3x^2-8x+2&=&0\\
3\left(x^2-\frac{8}{3}x\right)+2&=&0\\
3\left(x-\frac{4}{3}\right)^2-3\times \left(\frac{4}{3}\right)^2&=&-2\\
3\left(x-\frac{4}{3}\right)^2-\frac{16}{3}&=&-2\\
3\left(x-\frac{4}{3}\right)^2&=&\frac{10}{3}\\
\left(x-\frac{4}{3}\right)^2&=&\frac{10}{9}\\
x-\frac{4}{3}&=&\pm\frac{\sqrt{10}}{3}\\
x&=&\frac{4}{3}\pm \frac{\sqrt{10}}{3}\\
&=&\frac{4\pm \sqrt{10}}{3}
\end{eqnarray}\)
とすることもできますが、解の公式がなかった頃の昔に戻る必要はありません。
解の公式は覚えておきましょう。
（ウ）
変域問題です。
関数問題でグラフを書いて考えない人は解く気がない人です。
\(\displaystyle y=-\frac{2}{3}x^2\,(\,-3\,≦\,x\,≦\,2\,)\)
のグラフは
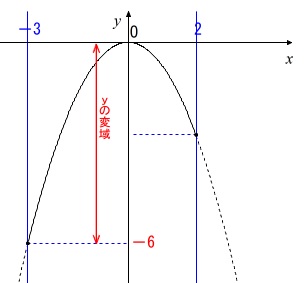\(\,y\,\)の変域に\(\displaystyle \,\left(\,2\,,\,-\frac{8}{3}\,\right)\,\)は関係ありません。
\(\,y\,\)の変域は \(\,-6\,≦\,y\,≦0\,\)
よって \(\,\underline{ a=-6\,,\,b=0 }\,\)
\(\,y\,\)の変域（値域）とは途中の変化に関係なく、
\(\,x\,\)の範囲（定義域）内で取り得る最小値と最大値の範囲のことです。
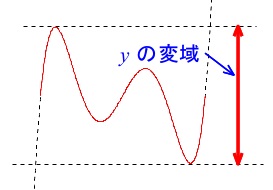
範囲があっても最大値最小値がない場合もありますが、詳しくは高校の数学で学びます。
（エ）
『\(\,12\,\)月の\(\,1\,\)か月間は』という問題部分は必要ありません。
\(\,3\,\)割引で買ったことには変わりありませんよ。
これくらいは問題文の意味を読み取らないと、いくら基本問題とは言っても難しく感じるでしょうね。
問題文を簡単にすると
\(\,a\,\)円の商品2つと\(\,b\,\)円の商品1つを\(\,3\,\)割引で買ったら\(\,5000\,\)円でおつりがでた。
となります。
\(\,3\,\)割\(\,\left(\displaystyle \frac{3}{10}\,\right)\)引きなので価格の\(\,\displaystyle \frac{7}{10}\,\)支払います。
\(\begin{eqnarray}\displaystyle
2a\times \frac{7}{10}+b\times \frac{7}{10}\,&＜&\,5000
\end{eqnarray}\)
商品代金より\(\,5000\,\)円の方が多かったからおつりが出るんですよ。
選択する答えの形にすると
\(\displaystyle \underline{ \frac{7}{10}(2a+b)\,＜\,5000 }\)
（オ）
数の大小を比較するときはやること決まっています。
『覚え太郎』会員は当たり前だろうけど、高校の数学でも同じですから安心して進学してください。
数の世界を統一します。（同じ数字の表し方をします。）
\(\color{red}{5\sqrt{3}}=\sqrt{5^2\times 3}=\color{red}{\sqrt{75}}\)
\(\color{blue}{8}=\sqrt{8^2}=\color{blue}{\sqrt{64}}\)
\(\color{magenta}{\sqrt{79}}\)
この3つの数字の大小比較です。
\(\color{blue}{\sqrt{64}}\,＜\,\color{red}{\sqrt{75}}\,＜\,\color{magenta}{\sqrt{79}}\)
答えるときはもとの与えられた数字で答える様に注意しておきましょう。
神奈川の場合は選択するだけだから気がつきますが、記述だともとの数字で答えるのを忘れることがあります。
\(\underline{ 8\,＜\,5\sqrt{3}\,＜\,\sqrt{79} }\)
（カ）
標本調査は比例式で終わりです。
\(\,500\,\)個中\(\,6\,\)個不良品があった。
\(\,30000\,\)個中だと不良品が何個あると推測できるか？
という比例です。
全数調査ではなくて推測でしかないので答えは「およそ」がつきます。
この問題では数値を選ぶだけですけどね。
\(\begin{eqnarray}
500:6&=&30000:x\\
500x&=&6\times 30000\\
x&=&\frac{6\times 30000}{500}\\
&=&\underline{ 360 }
\end{eqnarray}\)
『覚え太郎』会員で『約分の効用』見ていない人はいないでしょうねえ？笑
使わなければ高校数学でも宝の持ち腐れになりますよ。
問\(\,1\,\)と問\(\,2\,\)が終わりました。
他県に比べると小問集合の配点は低め？ですが、\(\,37\,\)点あります。
後にも基本問題は続きます。
今年は確率が割と楽だったかな？
後で解説します。
問\(\,3\,\)は平面図形の基本と\(\,1\,\)次方程式の立式です。
ちょっと見方を変えて、割り算の基本定理を利用すれば連立して簡単に出ます。
昨年の神奈川県立高校入試も傾向としては同じでしたね。
もちろん今年の出題も工夫されていますが、教科書の基本とその応用であることは変わりません。
クラブ活動で忙しい！
塾に通っているのに数学が苦手！
数学の勉強時間を減らしたい！
数学の勉強方法が分からない！
その悩み、『覚え太郎』が解決します！！！
