文字式の意味と金額や速さや時間などの関係の表し方と練習問題

文字式の意味と金額や速さなどの関係を文字式で表す表し方を練習問題の中で説明します。
数値だけで計算するのではなく、文字式のあつかいに慣れることで数学になじめるようになります。
文字式の表し方にはいくつかルールと呼べるものがありますので確認しておくと良いでしょう。
慣れてくれば文字式自体が数値のように感じてきます。

もちろん他の単元も大切ですが、２，３年生になって数学が苦手という人は、ほとんど（いや、全員と言っていい）この文字式が苦手です。
それくらい大切なところなので、今のうちから数学の基礎となる、この文字式には慣れておきましょう。

日本語を数学の言葉（文字式）に換える

文字式は数量を表す日本語を、数学の単語として文字を使って式で表したものです。
文字式を利用する場合は自分で勝手に使って良い文字と、やってはいけないことがあります。
細かいところは先に進んで確認していけば良いので、まずは簡単な文字式の表し方を覚えましょう。
練習問題の中で説明していきます。

割り算の基本（原則）

\(\large{\color{black}{\fbox{　2　}}}\)　次の数量を式で表せ。

実はこれ、割り算の基本性質なんです。

　\(　何かを 6　で割って、商が　m　で、余りが　 n　。\)

これは、１３を６で割ると、商が２、余りが１などと例をあげて考えると分かり易いのですが、
　\(　 13=6\times 2+1　となっています。\)

割り算するときの逆をたどれば良いだけですが、
小学生のクセが抜けない人が多いので間違って使う人が多いです。

　\( 6\,m\,+\,n\)

と表せます。
『覚え太郎』でもいっているけど、

元の数を　\(a\)　として、小学生みたいに、

　\(\displaystyle \frac{a}{6}=m \,\ldots \,n 　( 余り　n　)\)
なんてしないようにしましょう。

数学ではこのような表現はしません。

価格や値段（百分率）の文字式の表し方

％(パーセント)っていうのは百分率のことです。

つまり「１００の内いくつあるか」ということになります。

　\( \color{red}{　 x　％　なら\,10\,0の中に　x　だけある}\)
つまり、
　\( \color{red}{2000\,の中には　20\,\times x　ある}ということです。\)

この
　\(\color{red}{　 20\,x (円) \,分だけ引いて買った}んだから、\)

　\(　2000-20\,x\,（円）。これが答えです。\)

速さと時間と道のりの関係

「道のり」と「速さ」と「時間」の関係はしっかり覚えておきましょうね。

図の中で、３つの内１つが知りたければ、

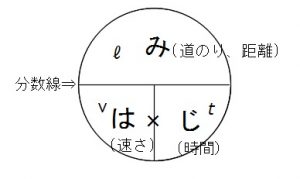
残りの２つで、図の通りの計算をすれば良いだけ。
（道のり）は？
といえば、残りの２つから
　\(　\color{red}{（道のり）＝（速さ）×（時間）}＝ v\times t\)
となり
（速さ）は？
残りの２つから
　\(　\color{red}{（速さ）＝（道のり）\div（時間）}＝　\displaystyle \frac{\ell}{t}\)
となります。

分数線は割り算を意味していますので、分数で表せば良いんです。

ここでは、道のりが知りたいので、
(速さ)×(時間)で計算すれば良いんだけど、
単位がそろっていません。
速さは時速、時間は分となっています。

計算するときは必ず単位をそろえなければなりません。
どっちにそろえるか？
答えはｋｍで答えなければならないので、２０分を時間に変えましょう。

１時間は６０分なので、
　\(\color{red}{　１分は　\displaystyle \frac{1}{60}　時間}\)

　\(　１０分は　 \displaystyle \frac{10}{60}　時間。\)

　\(　２０分は　\displaystyle \frac{20}{60}=\frac{1}{3}　時間\)

です。
だから表したい道のりは（速さ）×（時間）で、

　\( x\times \displaystyle \frac{1}{3}=\displaystyle \frac{x}{3}\, (\mathrm{km})\)

となります。

理科では秒をあつかうことが多いので秒への単位を変えることも慣れておきましょう。

\(\,1\,\)時間は\(\,60\,\)分、\(\,1\,\)分は\(\,60\,\)秒なので

　\(\,1時間=60\times 60=3600　(秒)\,\)

となります。

ここでは出てきていませんが、単位の換算、つまり、\(\mathrm{g}\)　を　\(\mathrm{kg}\)　に変えたり、
　\(\mathrm{m}\)　を　\(\mathrm{km}\)　に変えたりする練習は、やっておいて下さい。

\(\,\mathrm{\color{red}{k}}\,\)というのは\(\,\color{red}{1000}\,\)という意味を表しているので

　\(\,\mathrm{1\,kg=1000\,g}\,\)
　\(\,\mathrm{1\,km=1000\,m}\,\)

文字式は計算の一部として２年生にもう一度詳しくやりますが、

⇒　文字と数式の表し方と×や÷の省略の仕方と計算順序

文字式を表すときの約束がありますので確認しておいてください。

次は文字式に数値を代入するときのポイントと注意点です。

⇒　代入とは？文字式に代入するときのポイントと項と同類項(中学1年)

代入の仕方で計算ミスはかなり減ります。
関数の基本にもあるので確実にやっておきたいポイントになります。