2019年(平成31年)度東京都公立高校入試問題数学の規則性の解説

2019年(平成31年)度東京都で行われた公立高校入試数学第2問の規則性問題の解説です。
問1と問2がありますがどちらも図形を重ねたときの周囲の長さを文字式で表す問題で、規則性としては標準的な問題です。
ただ、差が出たとすればちょっとした作業量の違いだけでしょう。

問題は東京都も公開してくれています。

⇒　2019年東京都公立高校入試前期の数学問題

　\(\color{black}{\fbox{　2　}}\)

〔問\(\,1\,\)〕

問題文が長くて意味を取るのに時間がかかったかと思われますが、
この問題のルール（［きまり］）が読み取れれば問題自体は簡単です。

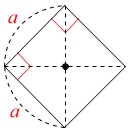
　正方形は\(\,1\,\)辺\(\,a\,\)の正方形

［きまり］①②③をまとめると、

　正方形の対角線の交点に次の正方形の1つの頂点を重ね、
　横向いたり、逆に重ねることなく対角線の交点は\(\,1\,\)直線上に次々に連なっていく。

ということが書かれているだけです。
図\(\,2\,\)、図\(\,3\,\)、図\(\,4\,\)のようになる以外に、途中で横向いたり逆に重なったりしないということです。

図\(\,1\,\)は正方形1つの場合で、
周りの長さは　\(\,\color{red}{4a}\,\)　です。

図\(\,2\,\)は正方形2つ（\(\,n=\color{blue}{2}\,\)）の場合で、
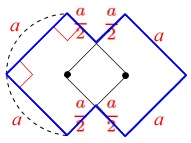周りの長さは各辺を加えていくと、

　\(\displaystyle 4a+\frac{a}{2}\times 4=\color{red}{6a}\)

図\(\,3\,\)は正方形3つ（\(\,n=\color{red}{3}\,\)）の場合で、
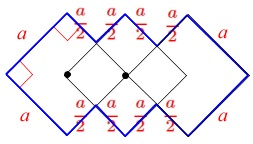周りの長さは各辺を加えていくと、

　\(\displaystyle 4a+\frac{a}{2}\times 8=\color{red}{8a}\)

となっています。

実はここまでで答えは出ているのですが、気がつかない人が多かったのではないでしょうか。

この問題は問\(\,2\,\)の誘導の一部でしかありません。
誘導内容となる一般的な\(\,\mathrm{L}\,\)の式はあとで説明しますが先に答えを出しておきましょう。

問題の\(\,n\,\)は\(\,2\,\)以上の自然数です。

　\(\,n=\color{blue}{2}\,\)のとき\(\,\mathrm{L}=\color{blue}{6a}\,\)
　\(\,n=\color{red}{3}\,\)のとき\(\,\mathrm{L}=\color{red}{8a}\,\)

これを満たしているのは、\(\,\underline{　エ　}\,\)だけです。

　アの\(\,4an\,\)は\(\,n=\color{blue}{2}\,\)のとき\(\,8a\,\)で一致しません。
　イの\(\,a(n+4)\,\)は\(\,n=\color{red}{3}\,\)のとき\(\,7a\,\)で一致しません。
　ウの\(\,2a(n+2)\,\)は\(\,n=\color{blue}{2}\,\)のとき\(\,8a\,\)で一致しません。
（\(\,n=\color{red}{3}\,\)のときも\(\,10a\,\)でダメです。）

　エは\(\,\mathrm{L}=2a(n+1)\,\)で

　\(\,n=\color{blue}{2}\,\)　のとき　\(\,\mathrm{L}=2a(2+1)=\color{blue}{6a}\,\)
　\(\,n=\color{red}{3}\,\)　のとき　\(\,\mathrm{L}=2a(3+1)=\color{red}{8a}\,\)

どちらも一致しています。
この問題での答えは選べても次につながらないのでこれを証明しておきます。

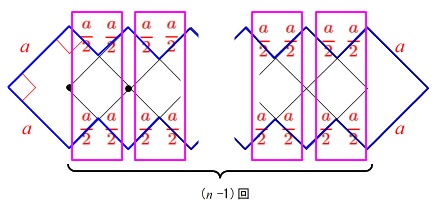\(\,n\,\)個の正方形を重ねたとき、

　両端の\(\,\color{red}{4a}\,\)は固定です。
　間の\(\color{magenta}{\fbox{　4辺　}}\)部分は1つの和が\(\,\displaystyle \frac{a}{2}\times 4=\color{red}{2a}\,\)です。
　\(\,n\,\)個の正方形を重ねると\(\color{magenta}{\fbox{　4辺　}}\)部分が\(\,(n-1)\,\)個あります。

なので
　\(\begin{eqnarray}
\mathrm{L}&=&4a+2a(n-1)\\
&=&4a+2an-2a\\
&=&2an+2a\\
&=&\underline{　2a(n+1)　}
\end{eqnarray}\)

または、
正方形をバラバラで考えたとき、重なって消える部分を引くことによっても求まります。
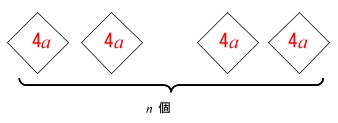正方形\(\,n\,\)枚分の週の長さは

　\(\,4a\times n=\color{blue}{4an}\,\)

重なって消える長さは1つの重なりで
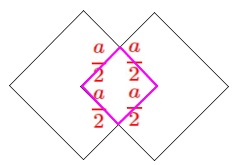　\(\displaystyle \frac{a}{2}\times 4=2a\)　消えます。

\(\,n\,\)個の正方形ではこれが\(\,n-1\,\)回重なるので、
重なって消える長さは
　
　\(2a\times (n-1)=\color{magenta}{2a(n-1)}\)

よって

　\(\begin{eqnarray}
\mathrm{L}&=&\color{blue}{4an}-\color{magenta}{2a(n-1)}\\
&=&4an-2an+2a\\
&=&2an+2a\\
&=&\underline{　2a(n+1)　}
\end{eqnarray}\)

どちらも似たようなものですね。

〔問\(\,2\,\)〕

今度は正方形が円になっただけです。

［きまり］は正方形の頂点が円周上の点になったことと、
対角線の交点が円の中心になったことだけで同じです。

〔問\(\,1\,\)〕と何が違うのか？　

何も違っていません。
ただし、ぼ～とながめているだけの人には同じに見えないでしょう。

説明は〔問\(\,1\,\)〕でしていることと同じになるので、長さだけ具体的に出していきます。

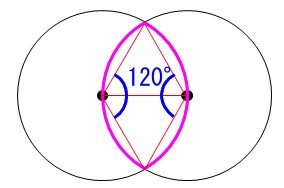重なりの部分です。

半径は常に等しいので赤い三角形は2つとも正三角形で、
片側の弧の中心角は\(\,120°\,\)です。

重なり部分の長さの片一方\(\,x\,\)は、周(\(\,360°\,\))の長さが\(\,\ell\,\)なので
比例式で表すと

　\(\begin{eqnarray}\displaystyle
360：\ell&=&120:x\\
360x&=&\ell \times 120\\
x&=&\ell \times \frac{120}{360}
\end{eqnarray}\)

それが2つあるので、
　\(\displaystyle \ell \times \frac{120}{360}\times 2\)

円が\(\,n\,\)個重なるとき重なり部分は\((\,n-1\,)\)個できるので

円\(\,n\,\)個の周の長さの和　\(\,\color{red}{n\times \ell}\,\)　から
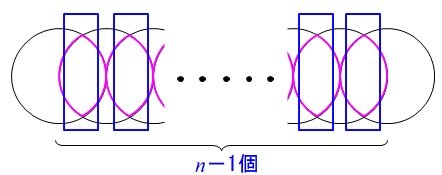重なり部分\(\,(n-1)\,\)個分
　\(\displaystyle \color{magenta}{\ell \times \frac{120}{360}\times 2\times (n-1)}\)
を引けば良いので

　\(\begin{eqnarray}\displaystyle
\mathrm{M}&=&\color{red}{\ell \times n}-\color{magenta}{\ell \times \frac{120}{360}\times 2\times (n-1)}\\
&=&n\ell-\frac{2}{3}n\ell+\frac{2}{3}\ell\\
&=&\frac{1}{3}n\ell+\frac{2}{3}\ell\\
&=&\underline{　\frac{1}{3}\ell(n+2)　}
\end{eqnarray}\)

これは〔問1〕の前半で説明したように、

　両端の長さ2つ
と
　重なり部分\(\,(n-1)\,\)個分の長さを足す

としても良いですが、両端の2つの計算は二度手間です。

この問題に惑わされる点といえば、
　半径\(\,r\,\)が与えられているのに\(\,r\,\)は必要ない
ということでしょうか。

あ、東京都の解答には\(\,r\,\)使ってました。笑
〔問\(\,1\,\)〕で説明した前半の考え方です。
（「二度手間」と書いてしまったけどそのままにしておきます。）

惑わされて良いんですね。
円周は\(\,\ell\,\)ではなく\(\,2\pi r\,\)を使って計算しています。
何のために\(\,\ell\,\)を与えたんだろう？

　\(\,2\pi r\,\)の関係式を作って、\(\,\ell\,\)に置きかえる

という部分も問題にしたのでしょう。

弧の長さは円周を基準にするので\(\,\ell\,\)の比例式で良いですよ。

〔問2〕の答えは『示せ』なので上で説明した計算式をそれぞれ書いて、
それなりの理由を書き足せば大丈夫です。

数学の解答は1つではありません。
答えは1つでも解法はいろいろあって良いですよ。
問題集の解答で1つしかないのは、1つしか思い浮かばなかったか、それがテーマの問題か、別解を示すのがめんどくさかったか、分かりません。

以上で　\(\color{black}{\fbox{　2　}}\)　は終わりです。

日本語が多くてとっつきにくいですけど、図を書いて作業を少し加えれば規則性も単純です。
捨てる問題ではないですね。\(\,12\,\)点だって。

〔問\(\,1\,\)〕の\(\,5\,\)点はおまけですね。笑

⇒　2019年度東京都公立高校入試 数学第3問関数問題の解説

\(\color{black}{\fbox{　3　}}\)は\(\,1\,\)次関数と\(\,2\,\)次方程式ですが、2次方程式までたどり着いていない人も多いかもしれません。
対称の意味を分かっていれば1つの文字設定で普通の関数問題になります。

⇒　東京都公立高校入試問題2019年(平成31年)度の数学の過去問解説

\(\color{black}{\fbox{　1　}}\)の解説です。
\(\color{black}{\fbox{　2　}}\)までで\(\,58\,\)点です。

\(\color{black}{\fbox{　5　}}\)が異様に簡単だったので『覚え太郎』会員は\(\,9\,\)割は取りたいですね。