2019年(平成31年)度東京都で行われた公立高校入試数学第3問の関数問題の解説です。
関数問題ですが1次関数だけを取り上げています。2次関数は入っていません。
差がつくと思われる座標を求める問題は、対称の性質を利用すると分かり易いです。
問題は東京都も公開してくれています。
\(\color{black}{\fbox{ 3 }}\)
〔問\(\,1\,\)〕
直線\(\,\ell\,\) : \(\,y=-x+9\,\)
直線\(\,\ell\,\)と\(\,x\,\)軸との交点を\(\,\mathrm{A}\,\)
\(\,\mathrm{P}\,\)は直線\(\,\ell\,\)上の点
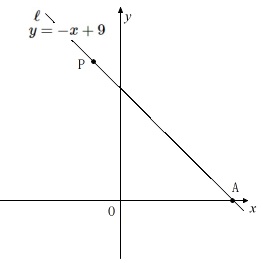
これは問題すべてに通じる条件です。
問題の図には書いてありませんが、\(\,x,y\,\)切片の両方を書き込んでおきます。
\(\,x\,\)軸との交点を\(\,x\,\)切片、\(\,y\,\)軸との交点を\(\,y\,\)切片といいます。
普通に切片といっているのは\(\,y\,\)切片のことです。
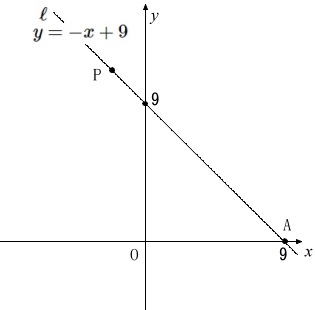
〔問\(\,1\,\)〕
\(\,\mathrm{P}\,\)の\(\,x\,\)座標が\(\,-4\,\)のとき\(\,\mathrm{P}\,\)の\(\,y\,\)座標はを求めます。
つまり、
\(\,y=-x+9\,\)において\(\,x=-4\,\)のときの\(\,y\,\)の値を求めよ。
ということです。
\(\begin{eqnarray}
y&=&-x+9\\
&=&-(-4)+9\\
&=&4+9\\
&=&\underline{ 13 }
\end{eqnarray}\)
〔問\(\,2\,\)〕
図\(\,2\,\)の条件が書かれています。
\(\,\mathrm{P}\,\)の\(\,x\,\)座標は\(\,9よ\,\)り小さい正の数
\(\,\mathrm{B}\,\)は\(\,y\,\)軸上で\(\,y\,\)座標が\(\,-3\,\)
\(\,\mathrm{Q}\,\)は軸を\(\,y\,\)軸とする\(\,\mathrm{P}\,\)と対称な点
\(\,\mathrm{B,Q}\,\)を通る直線を\(\,m\,\)とする。
言い換えると上の3つは
\(\,\mathrm{P}\,\)の\(\,x\,\)の範囲は\(\,0\,＜\,x\,＜\,9\,\)
\(\,\mathrm{B}\,\)の座標は\(\,(\,0\,,\,-3\,)\,\)
\(\,\mathrm{Q}\,\)は\(\,\mathrm{P}\,\)と\(\,y\,\)座標が同じで\(\,x\,\)座標は符号が逆で絶対値が同じ
ということです。
①は、
『点\(\,\mathrm{P}\,\)の座標が\(\,(\,2\,,\,7\,)\,\)のとき、
直線\(\,m\,\)の式を求めよ。』
です。
\(\,\mathrm{P}\,\)が\(\,(\,2\,,\,7\,)\,\)のとき
\(\,\mathrm{Q}\,\)の座標は\(\,(\,-2\,,\,7\,)\,\)
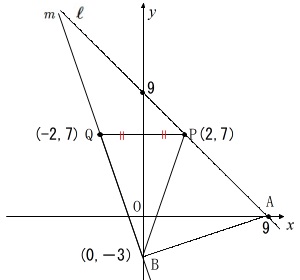
なので直線\(\,m\,\)は\(\,\mathrm{B,Q}\,\)を通るので、
\(\,(\,-2\,,\,7\,)\,\)
\(\,(\,0\,,\,-3\,)\,\)
を通る直線です。
\(\,(xの増加量)=0-(-2)=2\,\)
\(\,(yの増加量)=-3-(7)=-10\,\)
\(\,1\,\)次関数では変化の割合が傾きに一致するので、
傾きは \(\displaystyle \frac{-10}{2}=-5\)
このとき\(\,m\,\)は切片を\(\,-3\,\)とすると分かっているので
\(\,y=\underline{ -5x-3 }\,\)
②
\(\,\mathrm{△BPQ}\,\)の面積が\(\,\mathrm{△BAP}\,\)の面積の\(\,2\,\)倍になるときの点\(\,\mathrm{P}\,\)の座標です。
\(\,\mathrm{PQ}\,\)と\(\,y\,\)軸との交点を\(\,\mathrm{R}\,\)とすると
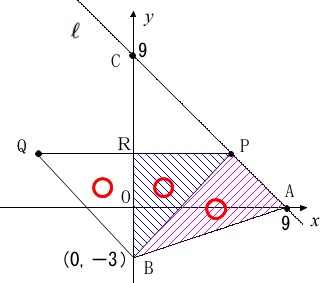
\(\,\mathrm{△BPQ=\color{blue}{△BPR}+\color{blue}{△BQR}}\,\)
また対称性から
\(\,\mathrm{\color{blue}{△BPR}=\color{blue}{△BQR}}\,\)
さらに、\(\,\mathrm{△BPQ}\,\)の面積が\(\,\mathrm{\color{magenta}{△BAP}}\,\)の面積の\(\,2\,\)倍になるときなので
\(\,\mathrm{\color{magenta}{△BAP}=\color{blue}{△BPR}}\,\)
のときの\(\,\mathrm{P}\,\)の座標を求めれば良いことになります。
座標を設定しましょう。
\(\,\mathrm{P}\,\)の\(\,x\,\)座標を求めたいので、\(\,\mathrm{P}\,\)の\(\,x\,\)座標を\(\,t\,\)とおきましょう。
\(\,\mathrm{P}\,\)は\(\,y=-x+9\,\)上の点なので\(\,x=t\,\)のとき\(\,y=-t+9\,\)
\(\,\color{red}{\mathrm{P}\,(\,t\,,\,-t+9\,)}\,\)
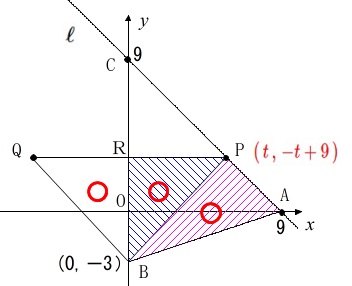\(\,\mathrm{\color{magenta}{△BAP}=\color{blue}{△BPR}}\,\)
を成り立たせるように線分の長さを書き出して行きます。
使わなくても分かるところは全部書き込んで良いですよ。
いくつか方法が浮かびますが、まずは計算が比較的楽な方法からやってみます。
\(\,\mathrm{△ABC}\,\)の面積は一定で、
\(\begin{eqnarray}\displaystyle
\mathrm{\color{blue}{△ABC}}&=&\frac{1}{2}\times \mathrm{CB}\times \mathrm{AO}\\
&=&\frac{1}{2}\times (9+3)\times 9\\
&=&\frac{1}{2}\times 12\times 9\\
&=&\color{blue}{54}
\end{eqnarray}\)
これを利用しましょう。
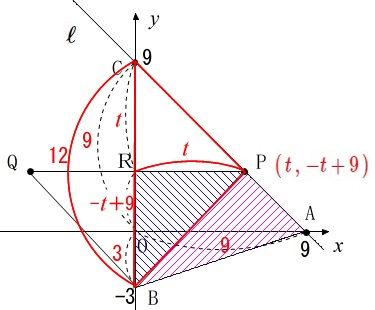
\(\begin{eqnarray}\displaystyle
\color{magenta}{\mathrm{△BAP}}&=&\mathrm{\color{blue}{△ABC}-\color{red}{△PCB}}\\
&=&\color{blue}{54}-\color{red}{\frac{1}{2}\times (9+3)\times t}\\
&=&\color{magenta}{54-6\,t}
\end{eqnarray}\)
これが\(\,\mathrm{△PBR}\,\)と等しいときの\(\,t\,\)を求めれば良いのです。
\(\begin{eqnarray}\displaystyle
\mathrm{\color{magenta}{△PBR}}&=&\frac{1}{2}\times \mathrm{BR}\times \mathrm{PR}\\
&=&\frac{1}{2}\times (-t+9+3)\times t\\
&=&\color{magenta}{\frac{1}{2}(-t+12)\,t}
\end{eqnarray}\)
より
\(\begin{eqnarray}\displaystyle
54-6\,t&=&\frac{1}{2}(-t+12)\,t\\
2(54-6\,t)&=&t\,(-t+12)\\
108-12\,t&=&-t^2+12\,t\\
t^2-24\,t+108&=&0\\
(t-6)(t-18)&=&0\\
t&=&6\,,\,18
\end{eqnarray}\)
\(\,t\,\)は\(\,\mathrm{P}\,\)の\(\,x\,\)座標で\(\,9\,\)より小さい正の数なので
\(\,t=18\,\)は不適で、\(\,t=\underline{ 6 }\,\)
他にも少なくとも3つは\(\,t\,\)を求める方法がありますが、
どうしましょう？
\(\,\mathrm{△ABC}\,\)の面積を使わない方法を1つだけやってみましょうか。
\(\,\mathrm{A\,(\,9\,,\,0\,)}\,\) \(\,\mathrm{B\,(\,0\,,\,-3\,)}\,\)
を通る直線は
\(\displaystyle y=\frac{1}{3}x-3\,\)
\(\,\mathrm{P}\,\)から\(\,y\,\)軸に平行な直線と\(\,\mathrm{AB}\,\)との交点を\(\,\mathrm{S}\,\)とすると、
\(\,\mathrm{S}\,\)は\(\,\mathrm{P}\,\)と\(\,x\,\)座標が同じで、
\(\displaystyle y=\frac{1}{3}x-3\,\)上の点になるので
\(\displaystyle \mathrm{S}\,\color{red}{\left(\,t\,,\,\frac{1}{3}\,t-3\,\right)}\,\)
このことと\(\,\mathrm{△BAP=△BPR}\,\)であることから
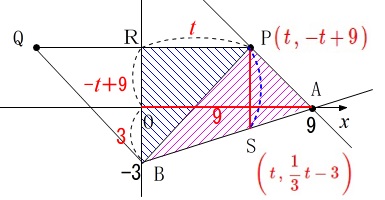\(\,\mathrm{△BAP}\,\)と\(\,\mathrm{△BPR}\,\)の面積を\(\,t\,\)を使って表します。
\(\begin{eqnarray}\displaystyle
\mathrm{\color{magenta}{△BAP}}&=&\frac{1}{2}\times \mathrm{PS}\times 9\\
&=&\frac{1}{2}\times \left\{-t+9-\left(\frac{1}{3}t-3\right)\right\}\times 9\\
&=&\frac{1}{2}\times \left(-t+9-\frac{1}{3}t+3\right)\times 9\\
&=&\frac{1}{2}\times \left(-\frac{4}{3}t+12\right)\times 9\\
&=&\color{magenta}{\frac{1}{2}(-12t+108)}
\end{eqnarray}\)
\(\begin{eqnarray}\displaystyle
\mathrm{\color{blue}{△BPR}}&=&\frac{1}{2}\times \{-t+9-(-3)\}\times t\\
&=&\frac{1}{2}\times (-t+12)\times t\\
&=&\color{blue}{\frac{1}{2}\,t\,(-t+12)}
\end{eqnarray}\)
これらが等しいことから
\(\begin{eqnarray}\displaystyle
\color{magenta}{\frac{1}{2}(-12t+108)}&=&\color{blue}{\frac{1}{2}\,t\,(-t+12)}\\
-12t+108&=&t(-t+12)\\
-12t+108&=&-t^2+12t\\
t^2-24t+108&=&0
\end{eqnarray}\)
この\(\,2\,\)次方程式を解けば同じ結果が得られます。
この方法だと具体的な面積は必要ありません。
いつまでもこの程度の関数で時間をかけるのはムダなので先に行きましょう。
文字の設定になれていない人は『超え太郎』の「座標と図形」をやり直してください。
宝の持ち腐れにはしないで下さい。
⇒ 東京都公立高校入試問題2019年(平成31年)度の数学の過去問解説
\(\color{black}{\fbox{ 1 }}\)は小問題集合です。
⇒ 2019年(平成31年)度東京都公立高校入試問題数学の規則性の解説
\(\color{black}{\fbox{ 2 }}\)は基本的な規則性問題でした。
⇒ 2019年度東京都公立高校入試 数学第4問平面図形問題の解説
\(\color{black}{\fbox{ 4 }}\)は平面図形の中でも平行四辺形で作る相似の古典的な問題です。
こういう問題が図形の基礎なのですよ。
クラブ活動で忙しい！
塾に通っているのに数学が苦手！
数学の勉強時間を減らしたい！
数学の勉強方法が分からない！
その悩み、『覚え太郎』が解決します！！！
