2019年(平成31年)度に東京都で行われた公立高校入試問題の数学の過去問解説です。
このページでは問1の小問集合の解説になります。
式の計算から方程式、確率、円周角、作図と基本の集合問題です。
嫌らしい問題がないのでここはささっと済ませたいところですが配点が高いので1つも落とせない問題です。
問題は東京都も公開してくれています。
\(\color{black}{\fbox{ 1 }}\)
〔問\(\,1\,\)〕
正の数負の数の簡単な計算問題ですが符号にだけは注意しておきましょう。
計算順序は算数と同じで、かけ算が先です。
\(\hspace{10pt}\displaystyle 5+\frac{1}{2}\times (-8)\\
=5-4\\
=\underline{ 1 }\)
〔問\(\,2\,\)〕
文字式の計算です。
（かっこ）を外す、同類項をまとめる、この2つを同時にやらないことが計算ミスを減らします。
\(\hspace{10pt} 4(a-b)-(a-9b)\\
=4a-4b-a+9b\\
=\underline{ 3a+5b }\)
〔問\(\,3\,\)〕
無理数の\(\,2\,\)乗展開計算です。
これは計算ミスを減らすために、暗算とていねいな展開計算とで見直しをしておくと良いですね。
暗算です。
\(\hspace{10pt} (\sqrt{7}-1)^2\\
=\underline{ 8-2\sqrt{7} }\)
展開公式
\(\color{red}{(a-b)^2=a^2-2ab+b^2}\)
の利用です。
\(\hspace{10pt}(\sqrt{7}-1)^2\\
=(\sqrt{7})^2-2\times \sqrt{7}\times 1+(1)^2\\
=7-2\sqrt{7}+1\\
=\underline{ 8-2\sqrt{7} }\)
もちろんこの公式利用は
\(\color{red}{(a+b)^2=a^2+2ab+b^2}\)
において
\(\hspace{10pt}(\sqrt{7}-1)^2\\
=(\sqrt{7})^2+2\times \sqrt{7}\times (-1)+(-1)^2\\
=7-2\sqrt{7}+1\\
=\underline{ 8-2\sqrt{7} }\)
としても同じです。
展開をていねいにすると
\(\hspace{10pt}(\sqrt{7}-1)^2\\
=(\sqrt{7}-1)(\sqrt{7}-1)\\
=(\sqrt{7})^2-\sqrt{7}-\sqrt{7}+1\\
=7-2\sqrt{7}+1\\
=\underline{ 8-2\sqrt{7} }\)
どれがおすすめとかありません。
この\(\,5\,\)点のためなら全部やります。
1つしか解説がないのは計算ミスは自分のせいだよといっているようなものです。
ただし、一通り解ける問題が全問が終わってからですよ。笑
『覚え太郎』会員にはいうまでもないことでしょう。
〔問\(\,4\,\)〕
簡単な\(\,1\,\)次方程式です。
展開と移項は同時にやらないことです。
\(\begin{eqnarray}
4x+6&=&5(x+3)\\
4x+6&=&5x+15\\
4x-5x&=&15-6\\
-x&=&9\\
x&=&\underline{ -9 }
\end{eqnarray}\)
検算は\(\,x=-9\,\)をもとの方程式に代入して成り立っていればいい。
左辺：
\(\hspace{10pt}4x+6\\
=4(-9)+6\\
=-36+6=-30\)
右辺：
\(\hspace{10pt}5(x+3)\\
=5\left\{(-9)+3\right\}\\
=5(-6)=-30\)
一致しているので間違いなく方程式を成立させます。
⇒ 方程式とは？方程式の解と移項とは？基本問題の解き方(中１数学)
『方程式を解く』ことと『方程式の解を求める』ことは同じことです。
〔問\(\,5\,\)〕
連立方程式です。
連立方程式の解き方の方針は一文字消去です。
\( \begin{cases}
\hspace{7pt} -x+2y=8 ･･･①\\ \\
\hspace{7pt} 3x-y=6 ･･･②
\end{cases}\)
消去する文字はどちらでもかまいません。
ここでは\(\,y\,\)を消去するために第\(\,2\,\)方程式（下の方程式）を\(\,2\,\)倍して両辺を足します。
\(\hspace{14pt}-x+2y=8\\
\underline{+)\hspace{4pt}6x-2y=12}\\
\hspace{16pt}5x\hspace{21pt}=20\\
\hspace{42pt}\color{red}{x=4}\)
この\(\,x=4\,\)をどれでも良いので\(\,y\,\)を含む方程式に戻します。
\(\,x=4\,\)を②に代入しましょう。
変形してからでも良いですがそのまま代入します。
\(\begin{eqnarray}
3x-y&=&6\\
3(4)-y&=&6\\
12-y&=&6\\
-y&=&6-12\\
&=&-6\\
\color{red}{y}&\color{red}{=}&\color{red}{6}
\end{eqnarray}\)
答え \(\,\underline{ x=4\,,\,y=6 }\,\)
もう一つの①に代入して成り立てば計算ミスもありません。
ここでは確認しませんが実際の試験会場ではした方が良いですよ。
〔問\(\,6\,\)〕
\(\,2\,\)次方程式です。
因数分解から試して見るのが普通ですが、定数項\(\,9\,\)に着目して
\(\color{black}{\fbox{ 1 × 9 }}\) \(\color{black}{\fbox{ 3 × 3 }}\)
の組み合わせに足して\(\,x\,\)の\(\,1\,\)次の項の係数\(\,+1\,\)を出すものはありませんので解の公式です。
\(\begin{eqnarray}\displaystyle
x&=&\frac{-1\pm \sqrt{(1)^2-4\times (1)\times (-9)}}{2\times 1}\\
&=&\frac{-1\pm \sqrt{1+36}}{2}\\
&=&\underline{ \frac{-1\pm \sqrt{37}}{2} }
\end{eqnarray}\)
解の公式は覚えていると思うのでチェックするのは利用する場合ですね。
〔問\(\,7\,\)〕
2019年度都立入試で唯一の確率問題です。
たぶん普通の受験生は\(\,3\,\)通の数の組み合わせを書いたと思われますが、樹形図でも良いです。
\(\color{black}{\fbox{1}}\),\(\color{black}{\fbox{2}}\),\(\color{black}{\fbox{3}}\),\(\color{black}{\fbox{4}}\),\(\color{black}{\fbox{5}}\)
この\(\,5\,\)枚から\(\,3\,\)枚を取り出し、
取り出した\(\,3\,\)つの数の積が\(\,3\,\)の倍数
になる確率です。
3つの数字の組み合わせは、取り出した順番を考えず（同時でも順番に取り出しても同じです）
\(\,(1,2,\color{red}{3})(1,2,4)(1,2,5)(1,\color{red}{3},4)(1,\color{red}{3},5)(1,4,5)\,\)
\(\,(2,\color{red}{3},4)(2,\color{red}{3},5)(2,4,5)\,\)
\(\,(\color{red}{3},4,5)\,\)
の\(\,10\,\)通りしかありません。
この中で積が\(\,3\,\)の倍数になるのは\(\,\color{red}{3}\,\)を含んでいる組み合わせなので、
求める確率は
\(\displaystyle \frac{6}{10}=\underline{ \frac{3}{5} }\)
ただ、この組み合わせと確率とが直結するのは数字が1つずつの場合だけなのでできれば樹形図を使って確実にしたいですね。
もちろん同じ数字を違う数字としてあつかえば良いですが、なれるまでに時間がかかるでしょう。
樹形図は\(\,60\,\)通りありますが、たかが\(\,1\,\)～\(\,5\,\)の数字を並べるだけの\(\,60\,\)通りです。
それほど時間はかかりません。その手間だけで\(\,5\,\)点です。
私は書きませんので自分で書いてみてください。笑
3つの数字の並べ方が分母
\(\color{black}{\fbox{3}}\)の入る数字の並べ方が分子
（\(\color{black}{\fbox{3}}\)の位置が\(\,3\,\)通りあることに注意して）
として
\(\displaystyle \frac{4\times 3\times 3}{5\times 4\times 3}=\underline{ \frac{3}{5} }\)
でも良いですよ。
〔問\(\,8\,\)〕
円周角の定理です。
条件は
\(\,\mathrm{AB}\,\)は直径
\(\,\mathrm{A,B,C,D}\,\)は円周上の点
\(\,\mathrm{∠BAD=25^{\circ}}\,\)
直径に対する円周角が\(\,90°\,\)になることが分かれば終わりです。
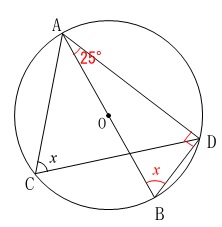\(\,\mathrm{\stackrel{\large{\frown}}{\mbox{AD}}}\,\)に対する円周角は等しいので、
\(\,\mathrm{∠ACD=∠ABD}=x\,\)
\(\,\mathrm{∠BAD=25^{\circ}}\,\)は問題に与えてくれているので、
\(\,\mathrm{△ABD}\,\)の内角の和が\(\,180°\,\)で1つの内角が\(\,90°\,\)であることから
\(\,\mathrm{∠BAD+∠ABD=90^{\circ}}\,\)
なので（残りの2つの角の和が\(\,90°\,\)で計算した方が楽です）
\(\begin{eqnarray}
25^{\circ}+x&=&90^{\circ}\\
x&=&90^{\circ}-25^{\circ}\\
&=&65^{\circ}
\end{eqnarray}\)
答え \(\,\underline{ 65 }\,\) 度
〔問\(\,9\,\)〕
作図ですが、垂線と二等辺三角形の描き方です。
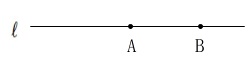
\(\,\mathrm{AB=AC}\,\)
\(\,\mathrm{∠CAB＝90^{\circ}}\,\)
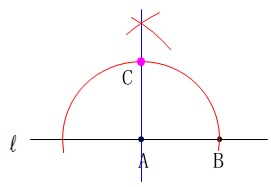
となる点\(\,\mathrm{C}\,\)の作図、つまり、直角二等辺三角形の作図ですね。
垂線を先に引いて、長さを等しくとっても良いですが、
同心円を\(\,2\,\)回書いているので、同じ円を利用できるように一気に仕上げてかまいません。
\(\color{black}{\fbox{ 1 }}\)はここまでです。
配点が\(\,46\,\)点ありました。
⇒ 2019年(平成31年)度東京都公立高校入試問題数学の規則性の解説
第\(\,2\,\)問は規則性の問題ですが、規則性の見方はいろいろあるので解答は1つではありません。
採点者はたいへんだと思います。笑
ところで、東京都では毎年、先生と\(\,\mathrm{S}\,\)さんが登場しますが、\(\,\mathrm{S}\,\)さんって誰？笑
\(\,SEITO\,\)の\(\,\mathrm{S}\,\)かな？
問題解くときにはどうでもいいことですけどね。
規則性の問題は全国にあります。
ポイントは1つです。
⇒ 2019年度東京都公立高校入試 数学第3問関数問題の解説
\(\color{black}{\fbox{ 3 }}\)は関数の問題です。
文字の設定だけで簡単に処理できますが、具体的な面積利用がはやいです。
⇒ 2019年度東京都公立高校入試 数学第4問平面図形問題の解説
\(\color{black}{\fbox{ 4 }}\)の相似比の利用はこの問題を繰り返せば良いと思える代表問題です。
⇒ 2019年度東京都公立高校入試 数学第5問立体問題の解説
\(\color{black}{\fbox{ 5 }}\)の立体は垂線の下りる位置だけ気をつければ難しくはありません。
ここにすべて書いてあります。
クラブ活動で忙しい！
塾に通っているのに数学が苦手！
数学の勉強時間を減らしたい！
数学の勉強方法が分からない！
その悩み、『覚え太郎』が解決します！！！
