埼玉県で2019年(平成31年)度に行われた公立高校入試問題のうち学校選択問題の数学の問題と解説です。
昨年同様一般入試問題との重複問題もありますので長くなりますが最後まで一気に行きます。
学校選択問題は少し問題量と計算量は増えますが基本的な方針は変えなくて良いです。
選択問題を選んでいる時点である程度は力はあるものとして簡単に済ませます。
方針の立て方やもう少し詳しい解説が必要と感じたら昨年度の解説も参考にしてみて下さい。
過去問を対策に利用する場合、問題を見て、手を動かしながら進めた方が力になりますよ。
一般入試問題と同じ問題がありますのでここでは同じ説明はしません。
問題が進んだ時点で解説先をお伝えします。
\(\,\large{1}\,\)
(1)文字式の計算です。
加法減法がありませんので分数線を大きく1つ書くだけでかなり変わります。
\(\hspace{10pt}\displaystyle (-a)^3\div 2a^4\times \left(\frac{1}{2}a\right)^2\\
\displaystyle =\frac{(-a^3)\times a^2}{2a^4\times 2^2}\\
\displaystyle =-\frac{a^3\times a^2}{2a^4\times 4}\\
\displaystyle =-\frac{a^5}{8a^4}\\
\displaystyle =\underline{ -\frac{a}{8} }\)
なんだか見にくいのでやはり割り算は逆数のかけ算として処理します。
\(\hspace{10pt}\displaystyle (-a)^3\div 2a^4\times \left(\frac{1}{2}a\right)^2\\
\displaystyle =\frac{(-a)^3}{1}\times \frac{1}{2a^4}\times \frac{a^2}{2^2}\\
\displaystyle =\underline{ -\frac{a}{8} }\)
分数線は\(\,1\,\)本でも良いですよ。
(2)
無理数の展開と有理化と加法が混じった計算です。
分数計算ですが、分数計算は算数と同じで良いです。
\(\hspace{10pt}\displaystyle \frac{(\sqrt{3}-\sqrt{2})^2}{6}+\sqrt{\frac{2}{3}}\\
\displaystyle =\frac{(3-2\sqrt{6}+2)}{6}+\frac{\sqrt{6}}{3}\\
\displaystyle =\frac{5-2\sqrt{6}+2\sqrt{6}}{6}\\
\displaystyle =\underline{ \frac{5}{6} }\)
有理化はできるものとして処理しています。
分母1つで分子の計算に集中するのは無理数でも文字式でも同じです。
(3)
\(\,(x+3)\,\)が共通しているように見えますが、展開して左辺にすべての項を集めた方がはやいです。
とにかく通っているヒマはないので、方程式の基本通り左辺に集めましょう。
\(\begin{eqnarray}
2x(x+3)&=&(x+3)^2\\
2x^2+6x&=&x^2+6x+9\\
2x^2+6x-x^2-6x-9&=&0\\
x^2-9&=&0\\
(x+3)(x-3)&=&0\\
x&=&\underline{ \pm 3 }
\end{eqnarray}\)
\(\,2\,\)行目の
\(2x^2\color{red}{+6x}=x^2\color{red}{+6x}+9\)
の時点で
\(x^2=9\)
と気がつくかもしれませんが、そんなこと考えずに左辺に集めることに突っ走った方がはやいでしょう。
4行目で \(x^2-9=0\) となった時点で
\(\begin{eqnarray}
x^2&=&9\\
x&=&\underline{ \pm 3 }
\end{eqnarray}\)
とするのは時間のロスはありません。
(4)
これは中学入試でよく見る算数問題です。
問題の中だけで通用する計算方法の定義をして計算させる問題です。
記号の位置にある数字を当てはめるだけです。
\(\,(\,a\,,\,b\,)\,\)
\(\,(\,c\,,\,d\,)\,\)
について
\(\hspace{10pt}(\,a\,,\,b\,)\,*\,(\,c\,,\,d\,)\\
=(\,ac-bd\,,\,ad+bc\,)\)
このまま数字を入れるだけです。
焦らず代入する位置を間違えないように気をつけるのがポイントです。
①
\(\hspace{10pt}(\,1\,,\,-2\,)\,*\,(\,3\,,\,1\,)\\
=(\,1\times 3-(-2)\times 1\,,\,1\times 1+(-2)\times 3\,)\\
=(\,3+2\,,\,1-6\,)\\
=\underline{ (\,5\,,\,-5\,) }\)
②
これは難しく考えず左辺を定義通り計算すれば良いだけです。
左辺は
\(\hspace{10pt}(\,x\,,\,y\,)\,*\,(\,2\,,\,3\,)\\
=(\,x\times 2-y\times 3\,,\,x\times 3+y\times 2\,)\\
=(\,2x-3y\,,\,3x+2y\,)\)
これが右辺と一致するように連立します。
\(\,(\,2x-3y\,,\,3x+2y\,)=(\,-17\,,\,7\,)\,\)
\( \begin{cases}
\hspace{7pt} 2x-3y=-17\\ \\
\hspace{7pt} 3x+2y=7
\end{cases}\)
これを解いて、
\(\,\underline{ x=-1\,,\,y=5 }\,\)
この連立方程式は解けるでしょう？
これが解けない状態で学校選択問題は先のことを考えると無謀です。
(5)は一般入試の1の(9)
(6)は一般入試の1の(10)
(7)は一般入試の2の(1)
(8)は一般入試の1の(11)
と同じです。
\(\,\large{2}\,\)
(1)は一般入試の2の(3)と同じです。
(2)は骨の折れる作業が待っていますが、問題の図をうまく使えば素早く終わります。
普通なら組み合わせを書きだす、でしょう。
余りによる類別を知っていればすぐに終わりますが、学校でこれを教えているとは思えないので書き出しでしょうか？
カードの並べ方を分かり易くしてくれているので類別しなさい、が出題者の意図でしょうね。
後で解法はお伝えしますが、
意地でも答えを出す、ということで組み合わせをすべて書き出します。笑
さすがに樹形図\(9\times 8\times 7=504\)通りは試験時間からもきついでしょう。
和が\(\,3\,\)で割り切れる組み合わせを数字の小さい順に並べます。
同じ数字を書くのはめんどうなので小さい順にだけ選ぶように気をつけて場合を分けておきます。
\(\,1\,\)を3つの数字の最小で使うとき残りの2つは
\(2-3 2-6 2-9\)
\(3-5 3-8\)
\(4-7\)
\(5-6 5-9\)
\(6-8\)
\(8-9\) （\(\,\color{red}{10}\,\)通り）
\(\,2\,\)を3つの数字の最小で使うとき残りの2つは
\(3-4 3-7\)
\(4-6 4-9\)
\(5-8\)
\(6-7\)
\(7-9\) （\(\,\color{red}{7}\,\)通り）
\(\,3\,\)を3つの数字の最小で使うとき残りの2つは
\(4-5 4-8\)
\(5-7\)
\(6-9\)
\(7-8\) （\(\,\color{red}{5}\,\)通り）
\(\,4\,\)を3つの数字の最小で使うとき残りの2つは
\(5-6 5-9\)
\(6-8\)
\(8-9\) （\(\,\color{red}{4}\,\)通り）
\(\,5\,\)を3つの数字の最小で使うとき残りの2つは
\(6-7\)
\(7-9\) （\(\,\color{red}{2}\,\)通り）
\(\,6\,\)を3つの数字の最小で使うとき残りの2つは
\(7-8\) （\(\,\color{red}{1}\,\)通り）
\(\,7\,\)を3つの数字の最小で使うとき残りの2つは
\(8-9\) （\(\,\color{red}{1}\,\)通り）
これ以上はありません。
以上 \(\,\underline{ 30 }\,\) 通り
別解です。
\(\,3\,\)で割った余りが\(\,+1\,\)の
\(\color{black}{\fbox{ 1 }}\) \(\color{black}{\fbox{ 4 }}\) \(\color{black}{\fbox{ 7 }}\)
のグループを\(\,\mathrm{\color{red}{A}}\,\)とします。
\(\,3\,\)で割った余りが\(\,+2\,\)の
\(\color{black}{\fbox{ 2 }}\) \(\color{black}{\fbox{ 5 }}\) \(\color{black}{\fbox{ 8 }}\)
のグループを\(\,\mathrm{\color{blue}{B}}\,\)とします。
\(\,3\,\)で割った余りが\(\,0\,\)の
\(\color{black}{\fbox{ 3 }}\) \(\color{black}{\fbox{ 6 }}\) \(\color{black}{\fbox{ 9 }}\)
のグループを\(\,\mathrm{\color{magenta}{C}}\,\)とします。
同じグループ\(\,3\,\)枚の場合は\(\,3\,\)の倍数になるので
\(\,\mathrm{\color{red}{A}-\color{red}{A}-\color{red}{A} 1-4-7}\,\)
\(\,\mathrm{\color{blue}{B}-\color{blue}{B}-\color{blue}{B} 2-5-8}\,\)
\(\,\mathrm{\color{magenta}{C}-\color{magenta}{C}-\color{magenta}{C} 3-6-9}\,\)
は\(\,1\,\)通りずつ組み合わせがあります。
ここからです。
3つの数の和が\(\,3\,\)で割り切れる、つまり\(\,3\,\)の倍数になるには
\(\,\mathrm{\color{red}{A}}\,\)のグループから\(\,1\,\)枚
\(\,\mathrm{\color{blue}{B}}\,\)のグループから\(\,1\,\)枚
\(\,\mathrm{\color{magenta}{C}}\,\)のグループから\(\,1\,\)枚
ずつ組み合わせる場合しかありません。
例えば、
\(\,\mathrm{\color{red}{A}}\,\)から\(\,2\,\)枚選んだとすると、
\(\,1+4=5 , 1+7=8 , 4+7=11\,\)
\(\,3\,\)で割った余りは必ず\(\,2\,\)となります。
これに組み合わせとして\(\,1\,\)枚加えるとき、
余りが\(\,2\,\)の\(\,\mathrm{\color{blue}{B}}\,\)グループや、
余りが\(\,0\,\)の\(\,\mathrm{\color{magenta}{C}}\,\)グループと組み合わせても、
余りが\(\,3\,\)になることはないので\(\,3\,\)の倍数にはなりません。
つまり、
同じグループから\(\,3\,\)枚選ぶか、
3つのグループから\(\,1\,\)枚ずつ選ぶ場合だけ、
が\(\,3\,\)の倍数になる、和が\(\,3\,\)で割り切れるということです。
同じグループから\(\,3\,\)枚選ぶ方法は、
\(\,\mathrm{A}\,\)から\(\,3\,\)枚か、\(\,\mathrm{B}\,\)から\(\,3\,\)枚か、\(\,\mathrm{C}\,\)から\(\,3\,\)枚
の\(\,\color{red}{3}\,\)通りでした。
\(\,\mathrm{\color{red}{A},\color{blue}{B},\color{magenta}{C}}\,\)から\(\,1\,\)枚ずつ選ぶ方法は、
\(\,\mathrm{\color{red}{A}}\,\)から\(\,1\,\)枚を選ぶのが\(\,1,4,7\,\)の\(\,3\,\)通り
その\(\,3\,\)通りすべてに対して
\(\,\mathrm{\color{blue}{B}}\,\)から\(\,1\,\)枚を選ぶのが\(\,2,5,8\,\)の\(\,3\,\)通り
さらに\(\,\mathrm{\color{red}{A},\color{blue}{B}}\,\)の組それぞれすべてに対して
\(\,\mathrm{\color{magenta}{C}}\,\)から\(\,1\,\)枚を選ぶのが\(\,3,6,9\,\)の\(\,3\,\)通り
あるので
\(3\times 3\times 3=\color{red}{27}\) 通り
よって\(\,3\,\)枚のカードの数字の和が\(\,3\,\)で割り切れる場合は
\(3+27=\underline{ 30 } (通り)\)
\(\,\large{3}\,\), \(\,\large{4}\,\) は一般入試問題と同じです。
目次から埼玉県に飛ぶとはやいです。
\(\,\large{5}\,\)
正四角錐の問題なので取り組み易いです。
(1)
長さに関係なく成り立つ合同の証明です。
正四角錐の条件を見ておきましょう。
\(\color{red}{\fbox{ 条件 }}\)
頂点を\(\,\mathrm{O}\,\)とする正四角錐
底面\(\,\mathrm{ABCD}\,\)は正方形
頂点\(\,\mathrm{O}\,\)から底面\(\,\mathrm{ABCD}\,\)に下ろした垂線との交点が\(\,\mathrm{H}\,\)
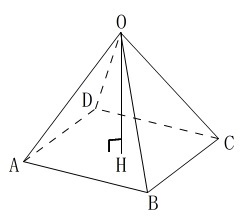直線と平面が垂直のとき、
平面内のどの直線とも垂線は直交します。
\(\,\mathrm{OH}\,\perp\,\mathrm{面\,ABCD}\,\)
なので、
\(\,\mathrm{OH\,\perp\,AC}\,\)
\(\,\mathrm{OH\,\perp\,BD}\,\)
また、\(\,\mathrm{H}\,\)は底面の正方形の対角線の交点にあります。
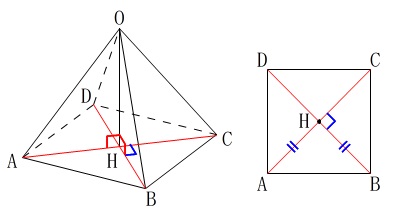(1)の証明には右の図は関係ありませんが、位置関係は意識しておくと良いですよ。
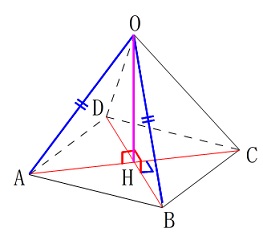
条件を図に書き込むと証明はすぐに終わります。
（証明）
\(\,\mathrm{△OHA}\,\) と \(\,\mathrm{△OHB}\,\) において
仮定から
\(\,\mathrm{\color{blue}{OA}=\color{blue}{OB} ･･･①}\,\)
\(\,\mathrm{OH}\,\)は垂線なので
\(\,\mathrm{\color{red}{∠OHA}=\color{red}{∠OHB}=\color{red}{90^{\circ}}} ･･･②\,\)
また共通の辺なので
\(\,\mathrm{\color{magenta}{OH}=\color{magenta}{OH} ･･･③}\,\)
①②③より
直角三角形において斜辺と他の\(\,1\,\)辺がそれぞれ等しい。
よって、
\(\,\mathrm{△OHA\,\equiv\,△OHB}\,\)（終わり）
合同条件は5つありますが「直角三角形の合同条件」を使う場合は、
角度が等しい条件には\(\,=90°\,\)まで書くようにしましょう。
(2)
長さの条件が加わります。
単位はすべて\(\,\mathrm{cm}\,\)なので省略します。
正方形\(\,\mathrm{ABCD}\,\)の\(\,1\,\)辺が\(\,6\,\)
\(\,\mathrm{OA=OB=OC=OD=6}\,\)
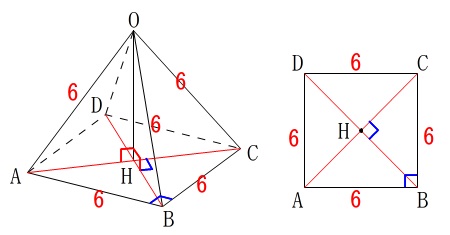
①線分\(\,\mathrm{OH}\,\)の長さを求めます。
立体のまま考えるのではなく、
求めたい線分\(\,\mathrm{OH}\,\)を含む面を抜き出します。
\(\,\mathrm{△OAH}\,\)でも\(\,\mathrm{△OAC}\,\)でも\(\,\mathrm{△OBD}\,\)でも\(\,\mathrm{OH}\,\)を含んでいるなら正四角錐の場合はかまいません。
分かり易くするため直角三角形となる△\(\,\mathrm{OAH}\,\)を抜き出します。
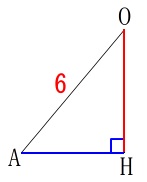\(\,\mathrm{OH}\,\)を求めたいので\(\,\mathrm{AH}\,\)が知りたい、となるので今度は\(\,\mathrm{AH}\,\)を含む面を抜き出します。
底面の正方形\(\,\mathrm{ABCD}\,\)です。
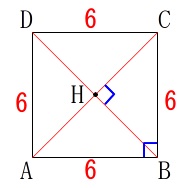対角線\(\,\mathrm{AC}\,\)の長さは三角定規の比からすぐに出ます。
\(\,\mathrm{\color{red}{AC}=\color{red}{6\sqrt{2}}}\,\)
なので
\(\begin{eqnarray}
\mathrm{AH}&=&\frac{1}{2}\times \mathrm{\color{red}{AC}}\\
&=&\frac{1}{2}\times \color{red}{6\sqrt{2}}\\
&=&\color{blue}{3\sqrt{2}}
\end{eqnarray}\)
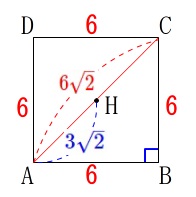\(\,\mathrm{△OAH}\,\)に戻りましょう。
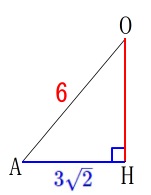
三平方の定理から
\(\begin{eqnarray}
\mathrm{AH^2+\mathrm{OH^2}}&=&\mathrm{OA^2}\\
(\color{blue}{3\sqrt{2}})^2+\mathrm{OH^2}&=&\color{red}{6^2}\\
18+\mathrm{OH^2}&=&36\\
\mathrm{OH^2}&=&36-18\\
&=&18\\
\mathrm{OH}&=&\pm 3\sqrt{2}
\end{eqnarray}\)
\(\,\mathrm{OH}\,\)は長さなので\(\,\mathrm{OH\,＞\,0}\,\)だから
\(\,\mathrm{OH=\underline{ 3\sqrt{2} }} (\mathrm{cm})\)
②
問題を簡単にすると、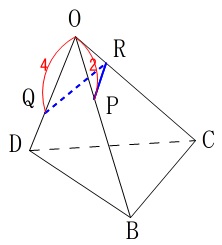
正四角錐を半分に切って、
\(\,\mathrm{OB}\,\)上の\(\,\mathrm{P}\,\)から\(\,\mathrm{AC}\,\)上の\(\,\mathrm{R}\,\)を結び、
さらに\(\,\mathrm{R}\,\)と\(\,\mathrm{OD}\,\)上の\(\,\mathrm{Q}\,\)を結ぶとき、
\(\,\mathrm{PR+RQ}\,\)が最短になるとき、
三角錐\(\,\mathrm{OPQR}\,\)の体積を求めよ。
そのときの長さが
\(\,\mathrm{OP=2 , OQ=4}\,\)
という条件付きです。
折れ線が最短になるときというのは、平面で見たときに直線になるときです。
これはよくある問題なので説明は必要無いかもしれませんが、簡単にしておきます。
展開図を書きます。
角の二等分線定理を使っても良いですがちょっと遠回りでしょうか。
単純な相似を使うのが良いですね。
四角形\(\,\mathrm{OBCD}\,\)は平行四辺形（ひし形）なので\(\,\mathrm{OB /\!/ DC}\,\)です。
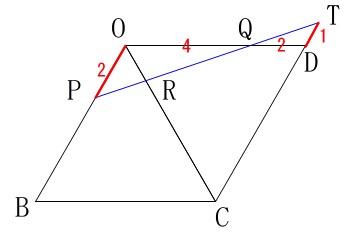ＰＱとＣＤの延長の交点を\(\,\mathrm{T}\,\)とすると
\(\,\mathrm{△OQP}\,\) ∽ \(\,\mathrm{△DQT}\,\)
相似比は\(\,\mathrm{OQ:DQ}\,\)の\(\,\mathrm{4:2\,=\,2：1}\,\)
だから
\(\,\mathrm{OP:DT=\color{red}{2}：\color{red}{1}}\,\)
正三角形の\(\,1\,\)辺なので\(\,\mathrm{DC=6}\,\)だから
\(\,\mathrm{CT=\color{red}{7}}\,\)
\(\,\mathrm{△ORP}\,\) ∽ \(\,\mathrm{△CRT}\,\)
で相似比は、\(\,\mathrm{OP:CT=2:7}\,\)なので
\(\,\mathrm{OR:CR}=\color{red}{2}:\color{red}{7}\,\)
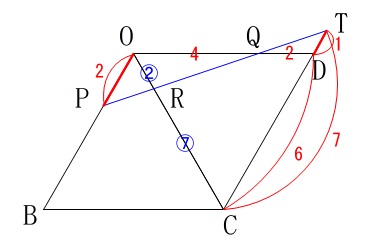
三角錐\(\,\mathrm{OBCD}\,\)の体積は正四角錐\(\,\mathrm{OABCD}\,\)の半分なので、
底面が正方形\(\,\mathrm{ABCD}\,\)の面積で\(\,\color{red}{36}\,\)、
高さが\(\,\mathrm{OH=\color{blue}{3\sqrt{2}}}\,\)だから
\(\begin{eqnarray}
(三角錐\,\mathrm{OBCD}\,)&=&\frac{1}{2}\times \frac{1}{3}\times \color{red}{36}\times \color{blue}{3\sqrt{2}}\\
&=&18\sqrt{2}
\end{eqnarray}\)
錐体に比を書き込むと
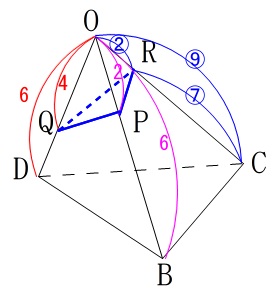
これから
\(\begin{eqnarray}
(三角錐\mathrm{OPQR})&=&18\sqrt{2}\times \frac{4}{6}\times \frac{2}{6}\times \frac{2}{9}\\
&=&18\sqrt{2}\times \frac{2}{3}\times \frac{1}{3}\times \frac{2}{9}\\
&=&\underline{ \frac{8\sqrt{2}}{9} } (\mathrm{cm})
\end{eqnarray}\)
とするのは『覚え太郎』向けの解答になるのでしょう。
普通に解いて見ましょう。
（今までの解説は何？）
ここまでは同じです。
\(\,\mathrm{Q}\,\)を通り、\(\,\mathrm{DC}\,\)に平行な直線と\(\,\mathrm{OC}\,\)との交点を\(\,\mathrm{S}\,\)とします。
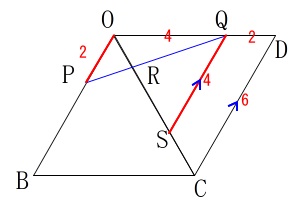
解答例で、『\(\,\mathrm{OS=4}\,\)となる点\(\,\mathrm{S}\,\)を取る』というのはこの\(\,\mathrm{S}\,\)のことですが、
長さを指定して点を取るなんてことは普通しません。
補助線は平行線か垂線を基本にしておけばいいので、この埼玉県の解答例は忘れて良いです。
（あ、ダメだといっているわけではなくて、相当な実力を持っていて、使える人は使って良いですよ。）
普通に公立入試で満点とる程度ならこんな特殊な設定をする必要はありません。
こういう設定をするのはトレミーの定理の証明のときくらいで良いです。笑
で問題を解きに戻りましょう。
相似から\(\,\mathrm{OR:SR=1：2}\,\)
は見抜けるでしょう。
\(\,\mathrm{△OCD}\,\)は正三角形で\(\,\mathrm{OC＝6}\,\)なので
\(\,\mathrm{OS:SC=4:2\,=\,2:1}\,\)
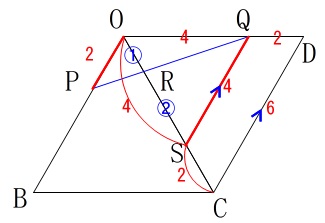
ところで、求めるのは\(\,\mathrm{OPRQ}\,\)の体積なので底面と高さを決めないと求まりません。
底面は\(\,\mathrm{△OPQ}\,\)として、高さは\(\,\mathrm{R}\,\)から\(\,\mathrm{△OPQ}\,\)に下ろした垂線の長さとします。
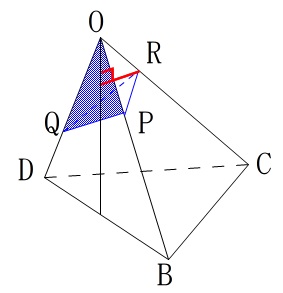
このときに気がつかなければならないのは、
\(\,\mathrm{OC}\,\)上の点から\(\,\mathrm{△OBD}\,\)に垂線を下ろすと、
\(\,\mathrm{OH}\,\)上に下りるということです。
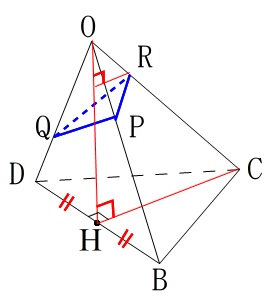
\(\,\mathrm{CH}\,\)は正方形の対角線の半分で\(\,\mathrm{AH=3\sqrt{2}}\,\)と同じです。
\(\begin{eqnarray}
\mathrm{OR:OC}&=&4\times \frac{1}{3}:6\\
&=&4:18\\
&=&2:9
\end{eqnarray}\)
これから\(\,\mathrm{R}\,\)から\(\,\mathrm{△OPQ}\,\)に下ろした垂線の長さ（高さ）は
\(\displaystyle 3\sqrt{2}\times \frac{2}{9}=\color{red}{\frac{2\sqrt{2}}{3}}\)
底面となる\(\,\mathrm{△OPQ}\,\)の面積は\(\,\mathrm{△OBD}\,\)を抜き出してみると、
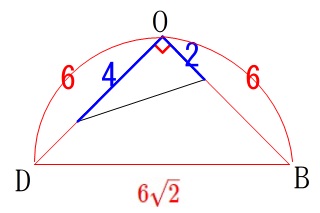
直角二等辺三角形の一部の面積なので
\(\begin{eqnarray}\displaystyle
\mathrm{△OPQ}&=&\frac{1}{2}\times \mathrm{OP}\times \mathrm{PQ}\\
&=&\frac{1}{2}\times 2\times 4\\
&=&\color{red}{4}
\end{eqnarray}\)
よって求める体積は
\(\begin{eqnarray}\displaystyle
(三角錐\mathrm{OPRQ})&=&\frac{1}{3}\times \color{red}{4}\times \color{red}{\frac{2\sqrt{2}}{3}}\\
&=&\underline{ \frac{8\sqrt{2}}{9} }
\end{eqnarray}\)
もちろん形だけ書いて計算は後回しで良いですよ。
高さを\(\,\mathrm{RI}\,\)とでもおいて、
\(\begin{eqnarray}\displaystyle
(三角錐\mathrm{OPRQ})&=&\frac{1}{3}\times \mathrm{△OPQ}\times \mathrm{RI}\\
&=&\frac{1}{3}\times \frac{1}{2}\times 2\times 4\times 3\sqrt{2}\times \frac{2}{9}\\
&=&\underline{ \frac{8\sqrt{2}}{9} }
\end{eqnarray}\)
答えは簡単に出せる問題ですが、説明が長くなってしまいました。
最初の方法で体積を計算できるようになってください。笑
これに集中すればできるようになります。
2019年度学校選択問題は以上です。
2019年度の埼玉県公立入試一般問題は確率も、データの活用（整理）も出ていないなんだか私立入試を解いているような偏った問題といって良いくらいでした。
（私立高校の全部が偏っているということではありません。私立ならあり得るということです。）
昨年度はバランス良く感じましたが、埼玉県はこういう問題構成だと思っておいた方が良いかもしれません。
試験時間を考えると、試験中考えている余裕はないでしょう。
普通の中学生では作業だけでもかなり時間がかかると思います。
\(\,2020\,\)年度以降はバランスの良い公立高校らしい問題構成が良いですよね。笑
クラブ活動で忙しい！
塾に通っているのに数学が苦手！
数学の勉強時間を減らしたい！
数学の勉強方法が分からない！
その悩み、『覚え太郎』が解決します！！！
