2018年(平成30年)度に高知県で行われた公立高校入試問題の数学の過去問解説です。
第6問までありますので、第1問から第3問までの前半と第4問から第6問までの後半に分けて説明します。
前半は広い範囲から取り上げられた基本問題の小問集合と第3問の平面図形の面積問題です。
高知県は50点満点ですが意識しておいて欲しい点がありますので確認しておいて下さい。
問題は高知県も公開してくれています。
\(\color{black}{\fbox{ 1 }}\)
\(\color{black}{\fbox{ 1 }}\)は正の数負の数、文字式、無理数の計算です。
(1)
正の数負の数の計算に限ったことではありませんが、
（かっこ）の中を計算することが先で、
（かっこ）を外す、計算するという二段階の計算を暗算しない
ことが計算ミスを減らしてくれます。
\(\hspace{10pt}-7-(-4)+1\\
=-7+4+1\\
=-3+1\\
=\underline{ -2 }\)
(2)
割り算は逆数のかけ算です。
この問題はそのままでも暗算でできなくはないでしょうが、割り算をかけ算に変えるとこまでは書いた方が良いです。
\(\hspace{10pt}\displaystyle (9x-6)\div \frac{3}{2}\\
\displaystyle =(9x-6)\color{red}{\times \frac{2}{3}}\\
\displaystyle =9x\color{red}{\times \frac{2}{3}}-6\color{red}{\times \frac{2}{3}}\\
=\underline{ 6x-4 }\)
分配もなれないうちはしっかり書いた方が良いかもしれないですね。
(3)
かけ算割り算が混じった計算では割り算部分を分母に回しましょう。
先ず符号を決定し、文字1つずつの順序で処理していけば良いですよ。
マイナス(-)は\(\,1\,\)回（奇数回）かけられていることになるので全体はマイナスです。
\(\hspace{10pt}\displaystyle 4ab^2\times (-6a)\div 8ab\\
\displaystyle =-\frac{4ab^2\times 6a}{8ab}\\
=\underline{ -3ab }\)
(4)
無理数の分母の有理化と足し算です。
この\(\,1\,\)問だけでも計算ミスは大きいので素因数分解もきっちりやっておいた方が良いです。
\(\hspace{10pt}\displaystyle \frac{12}{\sqrt{2}}+\sqrt{6}\times \sqrt{3}\\
\displaystyle =\frac{12\times \sqrt{2}}{\sqrt{2}\times \sqrt{2}}+\color{red}{\sqrt{18}}\\
\displaystyle =\frac{12\sqrt{2}}{2}+\color{blue}{3}\color{red}{\sqrt{2}}\\
=6\sqrt{2}+3\sqrt{2}\\
=\underline{ 9\sqrt{2} }
\)
ルートの中の\(\,18\,\)の素因数分解
\(\color{red}{2}\underline{\,)\,18}\\
\color{blue}{3}\underline{\,)\hspace{6pt}9}\\
\hspace{16pt}\color{blue}{3}\)
問題用紙のあいているところで確実にやっておいた方が良いですよ。
この問題は配点\(\,2\,\)点ですが\(\,50\,\)点満点なので\(\,4\,\)％、\(\,100\,\)点満点の\(\,4\,\)点分に相当します。
ミスは誰にでもありますので、いかに減らすかは自分次第です。
ここまでで\(\color{black}{\fbox{ 1 }}\)は終わりです。
\(\color{black}{\fbox{ 2 }}\)
\(\color{black}{\fbox{ 2 }}\)も小問集合です。
(1)代金を等式にして等式変形するだけです。
日本語の「は」は不等号を意味しますが、ここでは等号(=)です。
『 \(\,1\,\)本\(\,a\,\)円の鉛筆\(\,4\,\)本と\(\,1\,\)本\(\,b\,\)円のボールペン\(\,2\,\)本の代金
は
\(\,360\,\)円であった。 』
これを関係式にします。
\(\begin{eqnarray}
\color{blue}{4a+2b}&\color{red}{=}&\color{blue}{360}\\
2a+b&=&180
\end{eqnarray}\)
\(\,2a\,\)を移項して
\(\underline{ b=180-2a }\)
(2)
\(\,1\,\)次関数どうしの交点を求めます。
『交点』という日本語を数学の言葉に置きかえると『連立』です。
\( \begin{cases}\displaystyle
\hspace{7pt} y=-\frac{1}{2}x+2\\ \\
\hspace{7pt} y=3x+9
\end{cases}\)
交点は\(\,x,y座\,\)標とも2つの関数で一致します。
左辺は同じ\(\,y\,\)なので右辺どうしが等しくなります。
\(\begin{eqnarray}\displaystyle
-\frac{1}{2}x+2&=&3x+9\\
-x+4&=&6x+18\\
-x-6x&=&18-4\\
-7x&=&14\\
7x&=&-14\\
x&=&\color{blue}{-2}
\end{eqnarray}\)
どちらの\(\,1\,\)次関数に戻しても\(\,y\,\)座標は同じものが出てきます。
同じでなければ計算ミスしています。
\(\displaystyle y=-\frac{1}{2}x+2\)に\(\,\color{blue}{x=-2}\,\)を代入すると
\(\displaystyle y=-\frac{1}{2}\times (\color{blue}{-2})+2=\color{red}{3}\)
\(y=3x+9\)に\(\,\color{blue}{x=-2}\,\)を代入すると
\(y=3\times (\color{blue}{-2})+9=\color{red}{3}\)
これは連立方程式の解の確認方法と同じです。
問題は『座標を求めよ。』となっているので、
答えは \(\,\underline{ (\,-2\,,\,3\,) }\,\)
(3)比例の関数を求めます。
『\(\,y\,\)は\(\,x\,\)に比例し』、この時点で\(\,y=ax\,\)といていない『覚え太郎』会員はいないでしょう。笑
\(\,y=ax\,\)が\(\,(\,-4\,,\,6\,)\,\)を通るということなので、
\(\begin{eqnarray}\displaystyle
6&=&a\times (-4)\\
4a&=&-6\\
a&=&\frac{-6}{4}\\
&=&-\frac{3}{2}
\end{eqnarray}\)
この比例定数を求めることが問題ではありません。
『\(\,y\,\)を\(\,x\,\)の式で表せ。』
が問題の求める答えです。
問題はよく読んで答えを書きましょう。
答え \(\displaystyle \underline{ y=-\frac{3}{2}x }\)
(4)平方根についてです。
平方根が無理数だと考えがちですけど、違いますよ。
\(\,2\,\)乗して\(\,x\,\)になる数を\(\,x\,\)の平方根
というのです。
ア
\(\,64\,\)の平方根は\(\,\pm 8\,\)です。
\(8^2=64\)
\((-8)^2=64\)
正しい。
イ
\(\hspace{10pt}\sqrt{25}-\sqrt{16}\\
=5-4\\
=1\)
です。正しくありません。
\(\hspace{10pt}\sqrt{25}-\sqrt{16}\\
=\sqrt{25-16}\)
のようなルートの中身どうしの引き算はできません。
ウ
ルートの中身の計算が先です。
中学の数ではルートの中がマイナスにあることはありません。
\(\sqrt{(-7)^2}=\sqrt{49}=7\)
正しい。
アは平方根を聞いているので答えは2つになりますが、この問題は単にプラスの数のルートを外すだけなので答えは1つです。
ここを理解しいていない人が多いので教科書でも読み直しておくと良いです。
エ
無理数を\(\,2\,\)倍します。
無理数は文字式と同じだと考えて良いですよ。
\(\,2\,\)倍するのはルートの中身ではなく、無理数全体を\(\,2\,\)倍します。
\(\sqrt{3}\color{blue}{\times 2}\,=\,\color{blue}{2}\sqrt{3}\)
です。
\(\sqrt{3}\color{red}{\times 2}=\sqrt{3\color{red}{\times 2}}=\sqrt{6} (←ウソ計算です)\)
ではありません。
答え \(\,\underline{ ア , ウ }\,\)
(5)単なる変域問題ですが、関数の問題には変わりありません。
簡単にで良いのでグラフを書いておきましょう。
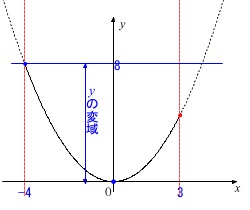定義域（\(\,x\,\)の変域）は\(\,-4\,≦\,x\,≦\,3\,\)ですが、
値域（\(\,y\,\)の変域）に\(\,x=3\,\)の値は関係ありません。
\(\,x=-4\,\) のとき \(\displaystyle y=\frac{1}{2}\times (-4)^2=8\,\)
なので最小値\(\,y=0\,\)から\(\,y\,\)の変域は
\(\,0\,≦\,y\,≦\,8\)
答え \(\,\underline{ a=0\,,\,b=8 }\,\)
(6)角度を求める問題です。
見逃してはいけないのは二等辺三角形という条件です。
\(\,\mathrm{ＡＢ＝ＡＣ}\,\)
\(\,\mathrm{ＣＤ＝ＣＥ}\,\)
\(\,\mathrm{∠BAC=44^{\circ}}\,\)
条件を図に書き込んで、それから分かることも書き込んで行けば自ずと答えは出てきます。
\(\,\mathrm{△ABC}\,\)は\(\,\mathrm{∠BAC}\,\)を頂角とする二等辺三角形なので、
\(\begin{eqnarray}
\mathrm{∠ABC}&=&∠\mathrm{ACB}\\
&=&\frac{180^{\circ}-44^{\circ}}{2}\\
&=&\frac{136^{\circ}}{2}\\
&=&68^{\circ}
\end{eqnarray}\)
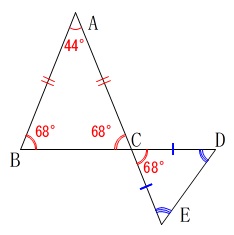次に \(\,\mathrm{△CED}\,\)は\(\,\mathrm{∠DCE}\,\)を頂角とする二等辺三角形なので、
\(\begin{eqnarray}
\mathrm{\color{red}{∠CDE}}&=&∠\mathrm{CED}\\
&=&\frac{180^{\circ}-68^{\circ}}{2}\\
&=&\frac{112^{\circ}}{2}\\
&=&\underline{ \color{red}{56^{\circ}} }
\end{eqnarray}\)
角度を求める問題は図の中で分かる角度を書き込んで行けば次々と見えてきます。
(7)円すいの展開図から底面の円の半径を求める問題です。
円すいでは母線が側面のおうぎ形の半径になります。
面積を利用することもできますが、分かっている長さが側面の直径なので、この直径から側面の弧の長さを出して、底面の半径につなげる方向で説明します。
側面の扇形は半円なので弧の長さは、
半径が\(\,6\,\)の円周の半分だから
\(\hspace{10pt}\displaystyle \frac{1}{2}\times 2\times \pi\times 6\,=\,\color{blue}{6\pi}\)
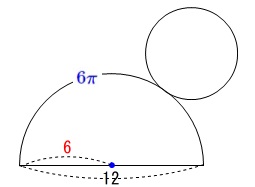ここで側面の扇形の弧の長さと、底面の円の周とは一致するので、
底面の半径を\(\,r\,\)とすると
\(\begin{eqnarray}
2\pi r&=&6\pi\\
r&=&\underline{ 3 }
\end{eqnarray}\)
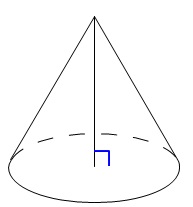ここから円すいの高さや体積を求めるよう指示されてもおかしくはない問題ですが、
この問題はここまでです。
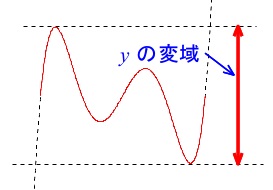
(8)ヒストグラムのデータの読み取りです。
問題を読み間違えなければ前半は必要ありません。
人数が度数なので最小目盛りの半分は整数の\(\,1\,\)になります。
ここで聞かれているのは
\(\,30\,\mathrm{m}\,\)以上\(\,40\,\mathrm{m}\,\)未満の生徒の人数の割合
です。
\(\,30\,\mathrm{m}\,\)以上\(\,35\,\mathrm{m}\,\)未満
ではありませんので、問題をしっかり読みましょう。
ヒストグラムを読み取ると、
\(\,30\,\mathrm{m}\,\)以上\(\,35\,\mathrm{m}\,\)未満の度数が\(\,\color{blue}{11}\,\)
\(\,35\,\mathrm{m}\,\)以上\(\,40\,\mathrm{m}\,\)未満の度数が\(\,\color{blue}{1}\,\)
なので
\(\,30\,\mathrm{m}\,\)以上\(\,40\,\mathrm{m}\,\)未満の度数は\(\,\color{blue}{11}+\color{blue}{1}=\color{red}{12}\,\)
\(\,12\,\)人は全体\(\,40\,\)人の何％か？
ということなので
\(\displaystyle \frac{12}{40}\times 100=\underline{ 30 (％) }\)
相対度数を聞いているわけでは無いので\(\,0.3\,\)と答えないようにしましょう。
(9)作図です。
作図で使える手法は、角の二等分線と垂線の引き方くらいで他に難しいことはあまり考えなくて良いです。
この問題が作図して欲しいのは、
\(\,\mathrm{A}\,\)と\(\,\mathrm{D}\,\)を重ねて折るときの折り目
その折り目と\(\,\mathrm{AB}\,\)との交点\(\,\mathrm{P}\,\)
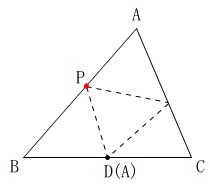です。
\(\,2\,\)点が重なる折り目となる直線は対称（線対称）の軸です。
つまり\(\,2\,\)点\(\,\mathrm{A,D}\,\)の垂直二等分線を引けば\(\,\mathrm{P}\,\)はすぐに分かります。
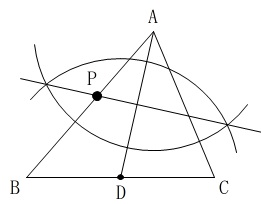これが答えです。
ここで\(\color{black}{\fbox{ 2 }}\)が終わりです。
注目して欲しいのはここまでで\(\,50\,\)点満点中\(\,26\,\)点、\(\,100\,\)点満点で見ると\(\,52\,\)点分あります。
基本をしっかりおさえていれば半分は確実に取れるということですね。
この年、平成\(\,30\,\)年度は平均点が\(\,21.8\,\)点でした。
\(\color{black}{\fbox{ 3 }}\)
手順が①②③とあります。
簡単に言えば図\(\,2\,\)で、
\(\,\mathrm{C}\,\)を中心に半径\(\,\mathrm{DC}\,\)で反時計回りに円を描き、
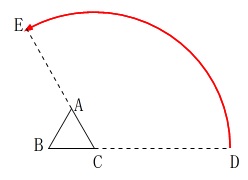\(\,\mathrm{E}\,\)までまわれば今度は\(\,\mathrm{AC}\,\)分半径が短くなり、
\(\,\mathrm{A}\,\)を中心に半径\(\,\mathrm{AE}\,\)で反時計回りに円を描き、
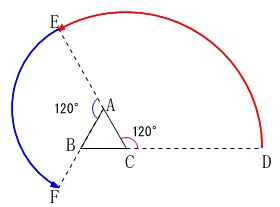\(\,\mathrm{F}\,\)までまわればさらに\(\,\mathrm{AB}\,\)分半径が短くなり、
\(\,\mathrm{B}\,\)を中心に半径\(\,\mathrm{BF}\,\)で反時計回りに円を描き\(\,\mathrm{C}\,\)に到達する。
ということで、
正三角形の1つの外角\(\,120°\,\)ごとに半径が変わっていることが分かります。
(1)\(\,\mathrm{A}\,\)を中心にまわるとき、
つまり半径\(\,\mathrm{AE}\,\)で中心角\(\,120°\,\)のおうぎ形の面積を求めることになります。
\(\,\mathrm{D}\,\)は最終的に\(\,\mathrm{C}\,\)にたどり着いています。
正三角形の\(\,1\,\)辺が\(\,4\,\)なので
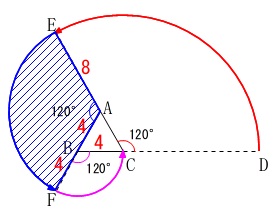
\(\,\mathrm{BC=BF=4}\,\)
\(\,\mathrm{AE=BF+AB=4+4=8}\,\)
だから求める面積は
\(\hspace{10pt}\displaystyle \pi \times 8^2\times \frac{120}{360}\\
\displaystyle =\underline{ \frac{64}{3}\pi (\mathrm{cm^2})}\)
(2)は正三角形の\(\,1\,\)辺が\(\,a\,\)のとき、
(1)と逆に\(\,\mathrm{C,F,E,D}\,\)とまわるときの弧の和を求めれば良いだけです。
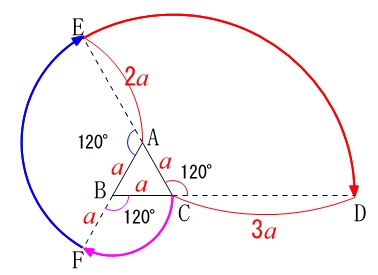
曲線\(\,\mathrm{\color{magenta}{CF}}\,\)は半径\(\,a\,\)で中心角が\(\,120°\,\)の扇形の弧
曲線\(\,\mathrm{\color{blue}{FE}}\,\)は半径\(\,2a\,\)で中心角が\(\,120°\,\)の扇形の弧
曲線\(\,\mathrm{\color{red}{ED}}\,\)は半径\(\,3a\,\)で中心角が\(\,120°\,\)の扇形の弧
なので曲線\(\,\mathrm{DEFC}\,\)の長さは
\(\hspace{10pt}\stackrel{\large{\frown}}{\mbox{CF}}+\stackrel{\large{\frown}}{\mbox{FE}}+\stackrel{\large{\frown}}{\mbox{FE}}\\
\displaystyle =2\pi\,a\times \frac{120}{360}+4\pi\,a\times \frac{120}{360}+6\pi\,a\times \frac{120}{360}\\
\displaystyle =\frac{2\pi\,a}{3}+\frac{4\pi\,a}{3}+\frac{6\pi\,a}{3}\\
\displaystyle =\frac{(2+4+6)\pi\,a}{3}\\
\displaystyle =\frac{(12)\pi\,a}{3}\\
=4\pi\,a\)
『言葉と式を使って説明せよ。』
となっていますが、式も数学の言葉なので、『日本語と式を使って』という意味です。
弧の長さを表すときにもっと詳しく書きたいなら、
半径\(\,r\,\)の円周は\(\,2\pi r\,\)なので
\(\hspace{10pt}\stackrel{\large{\frown}}{\mbox{CF}}+\stackrel{\large{\frown}}{\mbox{FE}}+\stackrel{\large{\frown}}{\mbox{FE}}\\
\displaystyle =\color{magenta}{2\pi\times a}\times \frac{120}{360}+\color{blue}{2\pi\times 2a}\times \frac{120}{360}+\color{red}{2\pi\times 3a}\times\frac{120}{360}\\
\displaystyle =\frac{2\pi\,a}{3}+\frac{4\pi\,a}{3}+\frac{6\pi\,a}{3}\\
\displaystyle =\frac{12\pi\,a}{3}\\
=4\pi\,a\)
としてももちろん良いですが、和を計算するので一つひとつ計算するのは手間です。
ダメなわけではありませんので普通に計算していいですが、
高校数学を見据えた『覚え太郎』会員は要領よく計算する方向で見ておいて下さい。
どのような計算をしても、
計算結果は\(\,4\pi\,a\,\)にならないと計算ミスしています。
ちなみに、この\(\color{black}{\fbox{ 3 }}\)は『超え太郎』の『平面図形』\(\,\mathrm{No.41}\,\)と同じですよ。
⇒ 2018年度高知県公立高校入試数学A問題の過去問解説(後半)
後半は確率、関数、平面図形です。
改めて感じるのは、
『覚え太郎』に専念した中学生は高校になっても数学が得点源ですね。
クラブ活動で忙しい！
塾に通っているのに数学が苦手！
数学の勉強時間を減らしたい！
数学の勉強方法が分からない！
その悩み、『覚え太郎』が解決します！！！
