2018年(平成30年)度に高知県で行われた公立高校入試問題の数学の過去問解説の後半です。
第4問から第6問までの解説になります。
後半はさいころ2つの確率と座標上の三角形の形状、関数総合、平面図形の問題がありますが、問題に与えられた図をうまく利用しましょう。
問題は高知県も公開してくれています。
\(\color{black}{\fbox{ 4 }}\)
さいころ2つを投げて出た目を座標上にとって、原点とでできる三角形の形状を見ます。
条件を整理しておきます。
\(\color{red}{\fbox{ 条件 }}\)
さいころ\(\,\mathrm{A}\,\)の出た目を\(\,\color{red}{a}\,\)
さいころ\(\,\mathrm{B}\,\)のでためを\(\,\color{blue}{b}\,\)
\(\,(\,\color{red}{a}\,,\,0\,)\,\)を\(\,\mathrm{P}\,\)
\(\,(\,\color{blue}{b}\,,\,\color{blue}{b}\,)\,\)を\(\,\mathrm{Q}\,\)
(1)
さいころ\(\,\mathrm{A}\,\)の出た目が\(\,6\,\)のとき、
つまり、\(\,\mathrm{P\,(\,6\,,\,0\,)}\,\)のとき\(\,\mathrm{△APQ}\,\)が直角三角形になる\(\,\mathrm{B}\,\)の出目をすべて求める問題です。
\(\,\mathrm{B}\,\)の出目\(\,b=1,2,3,4,5,6\,\)すべて見ます。
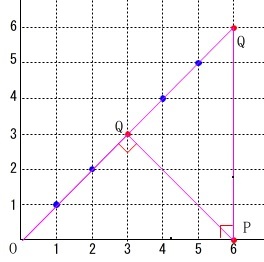\(\,b=3,6\,\)のとき
\(\,\mathrm{Q\,(\,3\,,\,3\,)\,,\,(\,6\,,\,6\,)}\,\)
このとき\(\,\mathrm{△OPQ}\,\)は直角三角形になります。
\(\,b=\underline{ 3 , 6 }\,\)
考えるよりすべて調べても\(\,6\,\)通りなので調べた方がはやいです。
(2)
\(\,\mathrm{△OPQ}\,\)の面積が\(\,\mathrm{6}\,\)となる組み合わせは何通りあるか？
三角形の面積なのでどちらかが偶数でなければ面積は\(\,6\,\)にはなりません。
しかし、偶数とか奇数を考えるより、
面積が\(\,6\,\)なら
\(\displaystyle \frac{1}{2}\times \color{red}{a}\times \color{blue}{b}=6\)
なので
\(\,\color{red}{a}\times \color{blue}{b}=\color{magenta}{12}\,\)
を考えた方がはやいです。
※
面積を計算して\(\,6\,\)になるものを探して全部計算してもそれほど変わりません。
さいころ2つの場合は樹形図よりも表ですね。
\(\begin{array}{|c|c|c|c|c|c|c|} \hline
& \color{blue}{\,1\,} & \color{blue}{\,2\,} & \color{blue}{3} & \color{blue}{4} & \color{blue}{5} & \color{blue}{6}\\ \hline
\color{red}{1} & 1 & 2 & 3 & 4 & 5 & 6\\ \hline
\color{red}{2} & 2 & 4 & 6 & 8 & 10 & \color{magenta}{12}\\ \hline
\color{red}{3 }& 3 & 6 & 9 & \color{magenta}{12} & 15 & 18\\ \hline
\color{red}{4} & 4 & 8 & \color{magenta}{12} & 16 & 20 & 24\\ \hline
\color{red}{5} & 5 & 10 & 15 & 20 & 25 & 30\\ \hline
\color{red}{6} & 6 & \color{magenta}{12} & 18 & 24 & 30 & 36\\ \hline
\end{array}\)
答え \(\,\underline{ 4 }\,\) 通り。
樹形図でも大して変わらないので樹形図でも良いですよ。
(3)
\(\,\mathrm{△OPQ}\,\)が鈍角三角形になる確率です。
三角形の形状は
鋭角三角形、直角三角形、鈍角三角形
しかありません。
直角三角形と鋭角三角形となる場合を引いても良いのですが、
試験中は迷っているヒマはないので鈍角三角形を探し尽くす方法で進めましょう。
\(\,a=1\,\)のとき\(\,b=1\,\)のとき直角三角形となります。
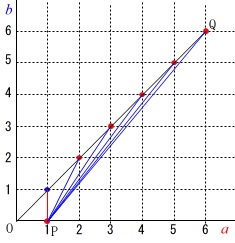鈍角三角形となるのは
\(\,b=2,3,4,5,6\,\) の\(\,\color{red}{5}\,\)通り
\(\,a=2\,\)のとき\(\,b=1,2\,\)のとき直角三角形になります。
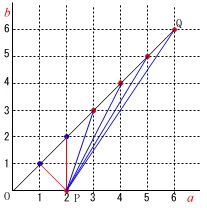鈍角三角形となるのは
\(\,b=3,4,5,6\,\) の\(\,\color{red}{4}\,\)通り
\(\,a=3\,\)のとき\(\,b=3\,\)のとき直角三角形になります。
\(\,b=2\,\)のときに鋭角三角形になるので注意して、
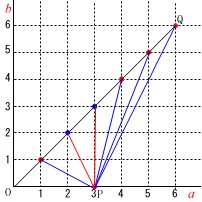鈍角三角形となるのは
\(\,b=1,4,5,6\,\) の\(\,\color{red}{4}\,\)通り
\(\,a=4\,\)のとき\(\,b=2,4\,\)のとき直角三角形になります。
\(\,b=3\,\)のときに鋭角三角形になるので注意して、
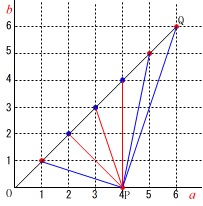
\(\,b=1,5,6\,\) の\(\,\color{red}{3}\,\)通り
\(\,a=5\,\)のとき\(\,b=5\,\)のとき直角三角形になります。
\(\,b=3,4\,\)のときに鋭角三角形になるので注意して、
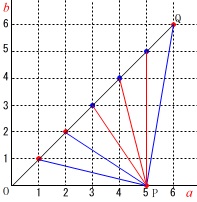
\(\,b=1,2,6\,\) の\(\,\color{red}{3}\,\)通り
\(\,a=6\,\)のとき\(\,b=3,6\,\)のとき直角三角形になります。
\(\,b=4,5\,\)のときに鋭角三角形になるので注意して、
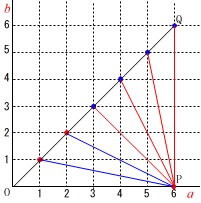
\(\,b=1,2\,\) の\(\,\color{red}{2}\,\)通り
よって鈍角三角形になるのは
\(\,\color{red}{5}+\color{red}{4}+\color{red}{4}+\color{red}{3}+\color{red}{3}+\color{red}{2}=\color{magenta}{21}\,\)通り
なので求める確率は
\(\displaystyle \frac{21}{36}=\underline{ \frac{7}{12} }\)
鋭角三角形の場合をどう見分けているかというと、
直角三角形と直角三角形の間にある部分、
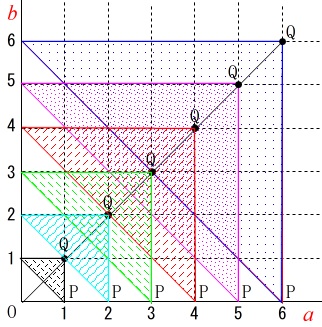\(\,a=1,2,3,4,5,6\,\)のそれぞれについて、
\(\,\mathrm{∠OPQ=90°}\,\)と\(\,\mathrm{P}\,\)を通り傾き\(\,-1\,\)の直線の間にある点では鋭角三角形
と見ているのですが、直感的でも良いと思いますよ。
（ちょっといい加減すぎかな？笑）
\(\color{black}{\fbox{ 5 }}\)
問題の条件から分かる座標は書き込みましょう。
\(\color{red}{\fbox{ 条件 }}\)
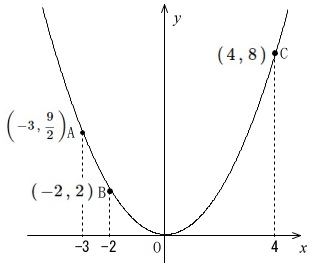
関数\(\displaystyle y=\frac{1}{2}x^2\)
\(\,\mathrm{A}\,\)の\(\,x\,\)座標は\(\,-3\,\)
\(\,\mathrm{B}\,\)の\(\,x\,\)座標は\(\,-2\,\)
\(\,\mathrm{C}\,\)の\(\,x\,\)座標は\(\,4\,\)
それぞれの座標は
\(\displaystyle \mathrm{A\,\left(\,-3\,,\,\frac{9}{2}\,\right)}\,\)
\(\,\mathrm{B\,(\,-2\,,\,2\,)}\,\)
\(\,\mathrm{C\,(\,4\,,\,8\,)}\,\)
(1)
すでに求めていますが、\(\,x=-2\,\)を\(\displaystyle \,y=\frac{1}{2}x^2\,\)に代入します。
\(\displaystyle y=\frac{1}{2}\times (-2)^2\,=\,2\)
よって点\(\,\mathrm{B}\,\)の座標は \(\,\underline{ (\,-2\,,\,2\,) }\,\)
(2)
\(\,2\,\)点\(\,\mathrm{A,C}\,\)を通る直線を求めます。
直線は異なる\(\,2\,\)点があれば必ず求まります。
\(\displaystyle \left(\,-3\,,\,\frac{9}{2}\,\right)\,\)
\(\,(\hspace{10pt}4\,,\,8\hspace{4pt})\,\)
直線の傾きは変化の割合に一致します。
\((\,x\,の増加量)=4-(-3)=\color{red}{7}\,\)
\((\,y\,の増加量)=\displaystyle 8-(\frac{9}{2})=\color{blue}{\frac{7}{2}}\,\)
これから傾きは
\(\displaystyle \frac{\color{blue}{\frac{7}{2}}}{\color{red}{7}}=\color{blue}{\frac{7}{2}}\div \color{red}{7}=\frac{7}{2}\times \frac{1}{7}=\frac{1}{2}\)
求める直線は\(\displaystyle \,y=\frac{1}{2}x+b\,\)とおけるので
\(\,\mathrm{A,C}\,\)のどちらかを代入すれば切片が求まります。
\(\,\mathrm{C\,(\,4\,,\,8\,)}\,\)を代入します。
\(\begin{eqnarray}
8&=&\frac{1}{2}\times (4)+b\\
&=&2+b\\
b&=&6
\end{eqnarray}\)
よって求める直線は
\(\displaystyle \underline{ y=\frac{1}{2}x+6 }\)
(3)
点\(\,\mathrm{D}\,\)が増えます。
\(\,\mathrm{D}\,\)の\(\,x\,\)座標は\(\,3\,\)なので
\(\displaystyle \,\mathrm{D\,\left(\,3\,,\,\frac{9}{2}\,\right)}\,\)
このとき直線\(\,\mathrm{BD}\,\)の傾きは\(\,\displaystyle \frac{1}{2}\,\)と書いてくれています。
直線\(\,\mathrm{AC}\,\)の傾きも\(\,\displaystyle \frac{1}{2}\,\)だったので、
この\(\,2\,\)直線は平行です。
『位置関係を利用する』とはこのことですね。
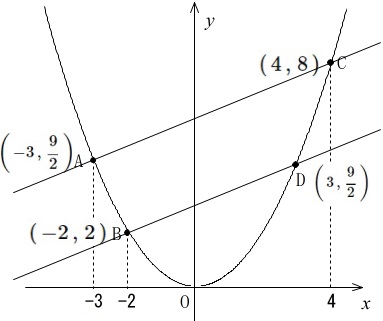問題は\(\,\mathrm{△ABD=△CBD}\,\)であることを説明することです。
\(\,2\,\)直線が平行であること
底辺\(\,\mathrm{BD}\,\)が共通であること
平行な直線上で頂点が移動しても面積は変わらないこと（等積移動）
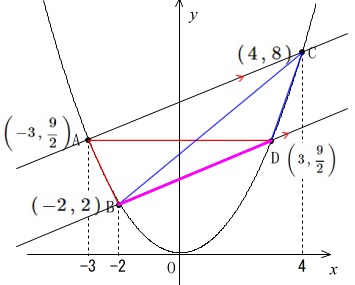
が言えていれば良いでしょう。
\(\color{black}{\fbox{ 6 }}\)
平面図形の問題ですが円の中にある三角形や平行線なので等しい角がたくさん出てきます。
条件を書き出します。
\(\color{red}{\fbox{ 条件 }}\)
\(\,\mathrm{AB=AC}\,\)となる円周上の点\(\,\mathrm{A,B,C}\,\)
\(\,\mathrm{D}\,\)は\(\,\mathrm{\stackrel{\large{\frown}}{\mbox{AC}}}\,\)上
\(\,\mathrm{BD}\,\)と\(\,\mathrm{AC}\,\)の交点を\(\,\mathrm{E}\,\)
\(\,\mathrm{F}\,\)は円周上の点で\(\,\mathrm{BD /\!/ FC}\,\)
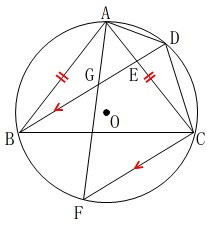平行線の錯角と円周角からすぐに終わるのでとっとと片づけます。
(1)
\(\,\mathrm{△ABG\,\equiv \,△ACD}\,\)を証明しますが、証明は図の中で終わらせておくことがポイントです。
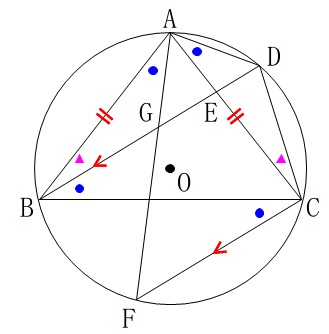他にも等しい角度はいろいろとありますがすでに証明できています。
（証明）
\(\,\mathrm{△ABG}\,\) と \(\,\mathrm{△ACD}\,\) において
同一弧の円周角は等しいので、
\(\,\mathrm{\stackrel{\large{\frown}}{\mbox{AD}}}\,\)の円周角から
\(\,\mathrm{\color{magenta}{∠ABG}=\color{magenta}{∠ACD} ･･･①}\,\)
\(\,\mathrm{\stackrel{\large{\frown}}{\mbox{BF}}}\,\)の円周角から
\(\,\mathrm{\color{blue}{∠BAG}=\color{red}{∠BCF} ･･･②}\,\)
\(\,\mathrm{\stackrel{\large{\frown}}{\mbox{DC}}}\,\)の円周角から
\(\,\mathrm{\color{blue}{∠CAD}=\color{red}{∠CBD} ･･･③}\,\)
平行線の錯角は等しいから
\(\,\mathrm{\color{red}{∠BCF}}=\mathrm{\color{red}{∠CBD}} ･･･④\,\)
ここで②③において④から
\(\mathrm{\color{blue}{∠BAG}}=\mathrm{\color{blue}{∠CAD}} ･･･⑤\)
また仮定から
\(\,\mathrm{\color{red}{AB}=\color{red}{AC} ･･･⑥}\,\)
①⑤⑥から
\(\,1\,\)組の辺とその両端の角がそれぞれ等しい
ので
\(\,\mathrm{△ABG\,\equiv \,△ACD}\,\) （終わり）
(2)
条件に長さが出てきます。
\(\,\mathrm{AB=8}\,\)
\(\,\mathrm{AD=3}\,\)
\(\,\mathrm{GF=7}\,\)
(1)で示した合同から、『対応する辺の長さは等しい』ので図に書き込みます。
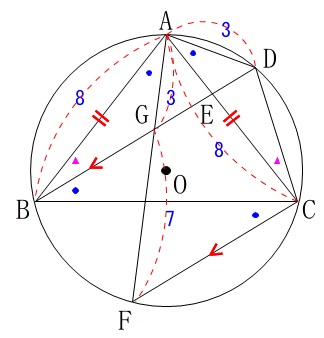求めるのは\(\,\mathrm{CE}\,\)の長さです。
長さを求めるときは、合同か相似か三平方の定理を先ずは使えないか考えるとほとんどうまくいきます。
\(\,\mathrm{GF=7}\,\)を使えるようにするためには\(\,\mathrm{B,F}\,\)を結ぶでしょう。
使わない条件、不要な条件はないので何故\(\,\mathrm{GF=7}\,\)があるのかを考えると良いです。
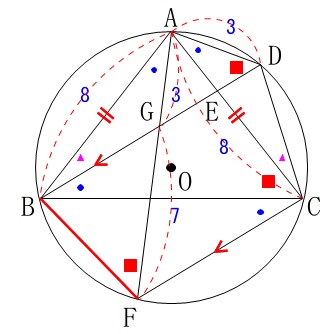\(\,\mathrm{\stackrel{\large{\frown}}{\mbox{AB}}}\,\)に対する円周角は等しいので、
\(\,\mathrm{\color{red}{∠BFA}=\color{red}{∠BCA}=\color{red}{∠BDA}}\,\)
\(\,\mathrm{CE}\,\)を含む三角形で相似を利用したいですが長さの情報が不足しています。
なので
\(\,\mathrm{△ABF}\,\) ∽ \(\,\mathrm{△AED}\,\)
を利用します。
先に\(\,\mathrm{AE}\,\)を求めて、\(\,\mathrm{AC}\,\)から引くことで\(\,\mathrm{CE}\,\)を求めます。
\(\,\mathrm{△\color{red}{A}\color{blue}{B}\color{magenta}{F}}\,\) ∽ \(\,\mathrm{△\color{red}{A}\color{blue}{E}\color{magenta}{D}}\,\)
から
\(\begin{eqnarray}\displaystyle
\mathrm{\color{red}{A}\color{blue}{B}:\color{red}{A}\color{blue}{E}}&=&\mathrm{\color{red}{A}\color{magenta}{F}:\color{red}{A}\color{magenta}{D}}\\
8:\mathrm{AE}&=&10:3\\
10\times \mathrm{AE}&=&3\times 8\\
\mathrm{AE}&=&\frac{3\times 8}{10}\\
&=&\frac{12}{5}
\end{eqnarray}\)
よって
\(\begin{eqnarray}\displaystyle
\mathrm{CE}&=&8-\frac{12}{5}\\
&=&\frac{40-12}{5}\\
&=&\underline{ \frac{28}{5} }
\end{eqnarray}\)
2018年度は以上です。
⇒ 2018年(平成30年)度高知県公立高校入試数学A問題の過去問解説
2018年度の高知県A問題の解説\(\color{black}{\fbox{ 1 }}\)から\(\color{black}{\fbox{ 3 }}\)です。
2019年度の問題解説はいつ更新できるか分かりませんのでこちらのまとめから確認してください。
クラブ活動で忙しい！
塾に通っているのに数学が苦手！
数学の勉強時間を減らしたい！
数学の勉強方法が分からない！
その悩み、『覚え太郎』が解決します！！！
