2019年(平成31年)度北海道公立高校一般入試数学第1問の解説

2019年(平成31年)度に北海道で行われた公立高校一般入試の数学第1問の解説です。
第1問は有理数や無理数、文字式の計算や変域、資料の活用、直角三角形の成立など小問集合になっています。
第2問からは裁量問題と重なるので第1問だけは分けて解説しておきます。

問題は北海道も公開してくれていますので正答とともに確認してください。

⇒　2019北海道一般入試問題

\(\large{\color{black}{\fbox{　1　}}}\)

問\(\,1\,\)
難しい計算はありませんので注意点だけ加えておきます。

(1)
　\(\hspace{10pt}7+(-5)\\
=7-5\\
=\underline{　2　}\)

（かっこ）を外した式は書いた方が計算ミスは減ります。
もっと項数が多い計算だと差がついてくるので気をつけておきましょう。

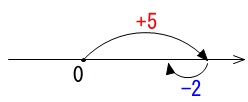
負の数を足すということは引き算と同じで、数直線上で左に移動します。

(2)
割り算は逆数のかけ算です。
どストレートすぎて戸惑ったかもしれませんね。笑

　\(\hspace{10pt}\displaystyle -4\color{red}{\div\frac{1}{9}}+8\\
=-4\color{red}{\times 9}+8\\
=-36+8\\
=\underline{　-28　}\)
(3)
無理数の計算ですが、項数が少ないのでかけ算してから素因数分解で良いでしょう。

　\(\hspace{10pt}\sqrt{6}\times \sqrt{2}-\sqrt{3}\\
=\sqrt{12}-\sqrt{3}\\
=2\sqrt{3}-\sqrt{3}\\
=\underline{　\sqrt{3}　}\)

無理数は2回かかると混合が外れるので
　\(\hspace{10pt}\sqrt{6}\times \sqrt{2}\\
=\sqrt{3}\times \sqrt{2}\times \sqrt{2}\\
=2\sqrt{3}\)
としてからでも良いですが、

　\(\underline{2\,)\,12}\\
\underline{2\,)\hspace{7pt}6}\\
\hspace{18pt}3\)

素因数分解は手を抜かず書いて確認しておきましょう。

問\(\,2\,\)
文字式の計算です。
（かっこ）を外した式を書いておくことが計算ミスを減らすのは文字式でも同じです。
特に引き算が混じる場合の符号の変化には注意しましょう。
ここでは引き算はありません。

　\(\hspace{10pt}4(2a+b)+(a-2b)\\
=8a+4b+a-2b\\
=\underline{　9a+2b　}\)

問\(\,3\,\)
変域問題は簡単にでも良いのでグラフを書いて考えた方が良いですよ。
ここでは\(\,1\,\)次関数なので変化は一定です。

関数は\(\,y=2x+1\,\)で定義域（\(\,x\,\)の変域）は\(\,1\,≦\,x\,≦\,4\,\)なので

　\(\,x=1\,\)のとき\(\,y=2\times (1)+1=3\,\)
　\(\,x=4\,\)のとき\(\,y=2\times (4)+1=9\,\)
なので値域（\(\,y\,\)の変域）は
　\(\,\underline{　3\,≦\,y\,≦\,9　}\,\)

問\(\,4\,\)

データが\(\,15\,\)個あります。
基本はちいさものから並べる、です。

しかしこの問題は最頻値だけ出せば良いので、並べなくても出すことはできます。

他の代表値を聞かれても良いように小さい順に並べる方法をとっておきます。

\(\,15\,\)個のデータを小さい順に並べると

　\(\,13,16,19,20,21,21,23,23,\color{red}{25},\color{red}{25},\color{red}{25},28,29,30,31\,\)　

確かに\(\,15\,\)個並びました。
このとき\(\,15\,\)個なければ並べ間違えています。

最頻値は度数が一番多い『値』です。

　\(\,\underline{　25　(回)　}\,\)

中央値を聞かれてもすぐに答えが出るのでデータが割と少ないときは並べ直すと良いです。

問\(\,5\,\)

\(\,3\,\)辺が直角三角形を作るかは、三平方の定理が成り立つかを見れば良いです。

そのとき三平方の定理をいちいち確認するのでなく、
\(\,3\,\)辺の平方数を書き出して、小さい方の2つの和が一番大きい数になっているかを確認すれば良いですよ。
それが三平方の定理が成り立つかの確認になっています。

一番大きい数字が斜辺の平方です。

ア
　\(2,7,8\)
平方数　\(\,4,49,\color{red}{64}\,\)
\(\,4+49=54\,\)

イ
　\(\,3,4,5\,\)
平方数　\(\,9,16,\color{red}{25}\,\)
　\(\,9+16=\color{red}{25}\,\)
一致しています。

ウ
　\(\,3,5,\sqrt{30}\,\)
平方数　\(\,9,25,\color{red}{30}\,\)
　\(\,9+25=34\,\)

エ
　\(\,\sqrt{2},\sqrt{3},3\,\)
平方数　\(\,2,3,\color{red}{9}\,\)
　\(\,2+3=5\,\)

オ
　\(\,\sqrt{3},\sqrt{7},\sqrt{10}\,\)
平方数　\(\,3,7,\color{red}{10}\,\)
　\(\,3+7=\color{red}{10}\,\)
一致しています。

問題にも『2つ選びなさい。』となっていますので間違いありません。

答え　\(\,\underline{　イ　と　オ　}\,\)

問\(\,6\,\)

これは教科書でたくさん練習しただろうから説明は必要無いと思いますが、
考え方としては相似ですよ。

平行線は良いですが、斜めの直線を移動させると
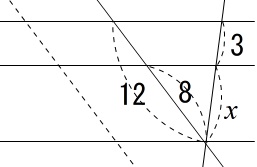相似な三角形が見えてくるでしょう？

確実にするにはニコちゃんマークですが必要ないでしょう。
記号打つのもめんどうだし比例式で求めます。

　\(\begin{eqnarray}
x:3&=&8:(12-8)\\
x:3&=&8:4\\
4x&=&3\times 8\\
x&=&\frac{3\times 8}{4}\\
&=&\underline{　6　}
\end{eqnarray}\)

または

　\(\begin{eqnarray}
x:(x+3)&=&8:12\\
12x&=&8(x+3)\\
12x&=&8x+24\\
12x-8x&=&24\\
4x&=&24\\
x&=&\underline{　6　}
\end{eqnarray}\)

どっちでも良いです。

\(\large{\color{black}{\fbox{　1　}}}\)はここまでです。
ここまでで\(\,60\,\)点満点中\(\,21\,\)点あります。

\(\large{\color{black}{\fbox{　2　}}}\)からは学校裁量問題と同じになります。

⇒　2019年度北海道公立入試裁量問題の解説 第1,2問(一般第2,3)

更新は過去問解説まとめで確認できます。

⇒　北海道の公立高校入試数学の過去問と解説

北海道の問題は裁量問題も含めてムラのない公立高校らしい問題です。

\(\,2018\,\)年度の問題を見てもわかるように、
広い範囲の基本を使いこなせるように何度も復習することが一番の対策になりますね。