2019年(平成31年)度に北海道で行われた公立入試裁量問題の数学第1問と第2問の解説です。
裁量問題の第1問,第2問は一般入試の第2問,第3問と同じです。
問題構成は因数分解、作図、確率、立体の体積を求める小問題集合と魔方陣と連立方程式の問題です。
問題は北海道も公開してくれていますので正答とともに確認してください。
一般入試問題と学校裁量問題は同じ問題があります。
\(\large{\color{black}{\fbox{ 1 }}}\)から\(\large{\color{black}{\fbox{ 4 }}}\)までは、一般入試問題と同じです。
\(\large{\color{black}{\fbox{ 1 }}}\) （一般入試問題\(\color{red}{\fbox{ 2 }}\)）
問\(\,1\,\)
因数分解です。
因数分解の手順は決まっています。
先ずは共通因数を抜き出します。
\(\hspace{10pt}2x^2-18\\
=2(x^2-\color{red}{9})\\
=2(x^2-\color{red}{3^2})\\
=\underline{ 2(x+3)(x-3) }\)
共通因数を抜き出した後\(\,(x^2-9)\,\)で終わらないように、
（かっこ）の中がまだ因数分解できないか確認を忘れないようにしましょう。
問\(\,2\,\)
作図です。
『\(\,3\,\)点\(\,\mathrm{A,B,C}\,\)から等しい距離にある点\(\,\mathrm{P}\,\)』
とは、
『\(\,3\,\)点\(\,\mathrm{A,B,C}\,\)を通る円の中心』
のことです。
2019年度の慶應義塾大学の入試でもテーマの一部として取り上げられていましたが高校の内容ではありません。
円は中心から等しい点の集まりということは小学校で習います。
\(\,2\,\)点から等しい点の集まりは垂直二等分線
これは中学の平面図形です。
このことから垂直二等分線を\(\,2\,\)本引いて交点を出せば終わりです。
円の中心は弦の垂直二等分線上
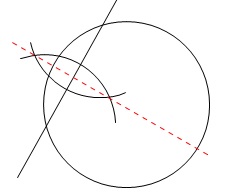
にあります。
しかし、1つの垂直二等分線上の点では定まりません。
もう一つの弦の垂直二等分線を引いて交点を定めればそれが円の中心です。
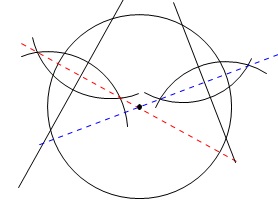つまり、
辺\(\,\mathrm{AB,BC,CA}\,\)の垂直二等分線の交点が\(\,\mathrm{P}\,\)
です。
このときに\(\,3\,\)本とも垂直二等分線を引く必要はありません。
\(\,2\,\)本の交点は必ず\(\,3\,\)本目も通るので\(\,2\,\)本で十分です。
どの\(\,2\,\)本を選ぶかは好きにしていいですよ。
ここでは\(\,\mathrm{AB}\,\)と\(\,\mathrm{AC}\,\)の垂直二等分線を引いて作図しておきます。
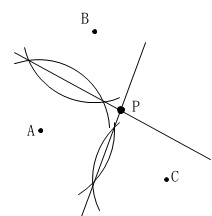\(\,\mathrm{AB}\,\)と\(\,\mathrm{BC}\,\)でも、\(\,\mathrm{AC}\,\)と\(\,\mathrm{BC}\,\)でも良いですよ。
問\(\,3\,\)
\(\,2\,\)けたの整数が\(\,4\,\)の倍数になる確率です。
問題はボールですが、カードでも何でも良いです。
4つの数字\(\,2,4,6,8\,\)が1つずつあり、2けたの整数を作ったときです。
もとにもどさずに\(\,2\,\)個取り出すので数字の重複はありません。
（\(\,22\,\)とか\(\,44\,\)などが無いということです。）
樹形図というかできる\(\,2\,\)けたの整数をすべて書き出した方がはやいです。
\(\,\color{red}{24} 26 \color{red}{28}\,\)
\(\,42 46 \color{red}{48}\,\)
\(\,62 \color{red}{64} \color{red}{68}\,\)
\(\,82 \color{red}{84} 86\,\)
\(\,2\,\)けたの整数は\(\,12\,\)通りしかなくて、
\(\,4\,\)の倍数は\(\,6\,\)通りあるので、
求める確率は
\(\displaystyle \frac{6}{12}=\underline{ \frac{1}{2} }\)
問\(\,4\,\)
円柱の高さを求めます。
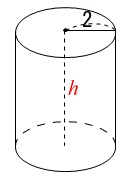底面の半径が分かっているので底面積はすぐに出ます。
柱体の体積は公式があります。
\(\color{red}{(柱体の体積)=(底面積)\times (高さ)}\)
底面は半径\(\,2\,\)の円なので
\(\,(底面積)=\pi\times (2)^2=4\pi\,\)
体積は問題に\(\,24\pi\,\)と与えられているので求める高さを\(\,h\,\)とおくと
\(\begin{eqnarray}
4\pi\times h&=&24\pi\\
h&=&\underline{ 6 (\mathrm{cm})}
\end{eqnarray}\)
\(\large{\color{black}{\fbox{ 2 }}}\) （一般入試問題 \(\color{red}{\fbox{ 3 }}\)）
縦と横の数字の個数が同じで、縦、横、斜めの数字（整数）の和が同じになるものを魔方陣といいますがどうでもいいです。笑
ここでは3つずつの数字の並びです。
図\(\,1\,\)で例を見てみましょう。
\(\begin{array}{|c|c|c|} \hline
8 & 1 & 6 \\ \hline
3 & 5 & 7 \\ \hline
4 & 9 & 2 \\ \hline
\end{array}\)
縦の和はすべて\(\,15\,\)
横の和もすべて\(\,15\,\)
斜めの和もすべて\(\,15\,\)
になっています。
中の数字は整数なので負の数が入ることもあります。
問\(\,1\,\)
9つの数字の縦、横、斜めの列のそれぞれの和が、
中央の数字の\(\,3\,\)倍になっていることの説明です。
図\(\,1\,\)の例では中央の数字は\(\,5\,\)でその\(\,3\,\)倍は\(\,15\,\)なので、
どの列も中央の数字の\(\,3\,\)倍になっています。
これを一般的に成り立っていることを文字を使って説明します。
ある\(\,1\,\)列に並んだ3つの数字の和を\(\,a\,\)とすると列は3つあるので
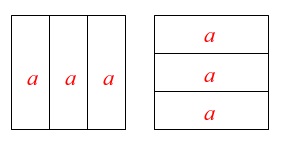9つのますに入っている数の和は
\(a+a+a=\underline{ 3a }\) \(\color{black}{\fbox{ ア }}\)
また、中央の数字を通る列は\(\,4\,\)列あるので
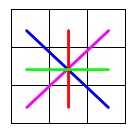\(\,4\,\)列分の和は\(\,\underline{ 4a }\,\) \(\color{black}{\fbox{ イ }}\)
ます全体の中央のますに入っている数を\(\,b\,\)とすると、
この\(\,4a\,\)は\(\,b\,\)を\(\,4\,\)回分数えているので、
（\(\,4\,\)列分の和\(\,4a\,\)は\(\,b\,\)を\(\,3\,\)回分余計に数えていることになるので）
9つのますに入っている数の和は\(\,4a-\underline{ 3b } \color{black}{\fbox{ ウ }}\,\)と表すことができます。
よって9つのますに入っている数は
\(\,3a\,\)と\(\,4a-3b\,\)と表される
ので
\(\begin{eqnarray}
3a&=&4a-3b\\
-a&=&-3b\\
a&=&3b
\end{eqnarray}\)
これはどの列の和も中央の数字の\(\,3\,\)倍になっていることを示しています。
問\(\,2\,\)
問\(\,1\,\)の「中央の数字」に惑わされてしまう気がしますが、
魔方陣では縦、横、斜めで同じ和にあるということだけで解決します。
左上のますには1つの数字が入るので、
左の縦と一番上の横の和は同じなので
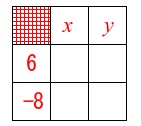
\(x+y=6+(-8) ･･･①\)
また中央の数字も1つの数字なので
真ん中の縦の列と斜めの列の和は同じだから
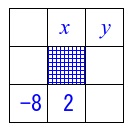
\(x+2=y+(-8) ･･･②\)
方程式は
\( \begin{cases}
\hspace{7pt} x+y=6+(-8) ･･･①\\ \\
\hspace{7pt} x+2=y+(-8) ･･･②
\end{cases}\)
少し整理して
\( \begin{cases}
\hspace{7pt} x+y=-2 ･･･③\\ \\
\hspace{7pt} x-y=-10 ･･･④
\end{cases}\)
でもいいです。
連立方程式を解いて
\(\hspace{18pt}x+y=\hspace{4pt}-2\\
\underline{-\,)\hspace{4pt}x-y=-10}\\
\hspace{30pt}2y=\hspace{10pt}8\\
\hspace{36pt}y=4\)
この\(\,y=4\,\)を①②③④どれでも良いので代入して\(\,x\,\)を求めます。
③に代入します。
\(\begin{eqnarray}
x+(4)&=&-2\\
x&=&-2-4\\
&=-6
\end{eqnarray}\)
答え \(\,\underline{ x=-6 , y=4 }\,\)
ここまでが学校裁量問題の \(\color{black}{\fbox{ 1 }}\) \(\color{black}{\fbox{ 2 }}\) と一般入試の \(\color{red}{\fbox{ 2 }}\) \(\color{red}{\fbox{ 3 }}\) です。
⇒ 2019年度北海道公立高校入試裁量問題の解説 第3,4問(一般第4,5)
関数の基本と座標設定問題です。
座標設定は簡単ですが1つだけ注意点があります。
⇒ 2019年(平成31年)度北海道公立高校一般入試数学第1問の解説
一般入試の \(\color{black}{\fbox{ 1 }}\) は小問集合です。
クラブ活動で忙しい！
塾に通っているのに数学が苦手！
数学の勉強時間を減らしたい！
数学の勉強方法が分からない！
その悩み、『覚え太郎』が解決します！！！
