2019年度北海道公立高校入試裁量問題の解説 第3,4問(一般第4,5)

2019年(平成31年)度に北海道で行われた公立高校入試裁量問題第3問と第4問の解説です。
裁量問題の第3問,第4問は一般入試の第4問,第5問と同じです。
第3問は関数の基本的な問と座標設定問題です。
第4問は平面図形の書くの大きさと合同の証明ですが、基本通りの作業で終わりますのでまとめて解説します。

問題は北海道も公開してくれていますので正答とともに確認してください。

⇒　2019北海道一般入試問題

一般入試問題と学校裁量問題は同じ問題があります。

⇒　2019年北海道学校裁量問題

\(\large{\color{black}{\fbox{　1　}}}\)から\(\large{\color{black}{\fbox{　4　}}}\)までは、一般入試問題と同じです。

\(\large{\color{black}{\fbox{　3　}}}\)　（一般入試問題\(\color{red}{\fbox{　4　}}\)）

関数は固定された放物線が2つあります。

　\(\displaystyle y=x^2　･･･①\)
　\(\displaystyle y=\frac{1}{3}x^2　･･･②\)

3つの点があります。

　\(\,\mathrm{A}\,\)は②のグラフ上で\(\,x\,\)座標が正
　\(\,\mathrm{B}\,\)は\(\,\mathrm{A}\,\)を通り\(\,y\,\)軸に平行な直線と①との交点
　\(\,\mathrm{C}\,\)は\(\,\mathrm{A}\,\)と\(\,y\,\)軸について対称な点

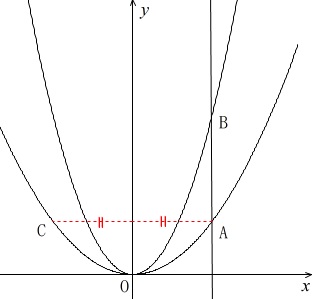
グラフで見るとわかりやすいですが、

　\(\,\mathrm{A}\,\)と\(\,\mathrm{B}\,\)は\(\,x\,\)座標が同じ
　\(\,\mathrm{A}\,\)と\(\,\mathrm{C}\,\)は\(\,y\,\)座標が同じ

ということです。

問\(\,1\,\)

『\(\,\mathrm{A}\,\)の\(\,x\,\)座標が\(\,2\,\)のとき』

\(\,\mathrm{A}\,\)は②上の点なので
　\(\,x=2\,\)のとき\(\,\displaystyle y=\frac{1}{3}\times (2)^2=\frac{9}{2}\)
つまり、
　\(\displaystyle \,\mathrm{A\,\left(\,2\,,\,\frac{9}{2}\,\right)}\,\)
のとき\(\,\mathrm{C}\,\)の座標は？という問です。

\(\,\mathrm{C}\,\)は\(\,\mathrm{A}\,\)と\(\,y\,\)軸対称なので、
　\(\,x\,\)座標の符号が反対で\(\,y\,\)座標が同じ点
です。

　\(\displaystyle \,\underline{　\mathrm{C\,\left(\,-2\,,\,\frac{9}{2}\,\right)}　}\,\)

問\(\,2\,\)

この問題は注意点が1つあります。

答えを求めるのは簡単なのですが、
　『\(\,2\,\)点\(\,\mathrm{B,C}\,\)を通る直線』
ではなく
　『\(\,2\,\)点\(\,\mathrm{B,C}\,\)を通る直線の傾き』
を求める問題です。

直線を答えに書いてしまいそうなくらい勢いよく解けるので、落ち着いて問題はよく読みましょう。

\(\,x=6\,\)のとき\(\,\mathrm{B}\,\)の\(\,y\,\)座標は\(\,y=(6)^2=36\,\)なので

　\(\,\mathrm{B\,(\,6\,,\,36\,)}\,\)

このときの\(\,\mathrm{A}\,\)の座標は、
　\(\,x=6\,\)　から　\(\displaystyle \,y=\frac{1}{3}\times (6^2)=12\,\)
なので
　
　\(\,\mathrm{A\,(\,6\,,\,12\,)}\,\)

この\(\,\mathrm{A}\,\)を\(\,y\,\)軸を軸に対称移動させて

　\(\displaystyle \,\mathrm{C\,(\,-6\,,\,12\,)}\,\)

よって\(\,\mathrm{B,C}\,\)を通る直線は

　\(\,(\,-6\,,\,12\,)\,\)
　\(\,(\hspace{10pt}6\,,\,36\,)\,\)

を通ります。

\(\,1\,\)次関数の傾きは変化の割合と一致するので、
傾きはこの\(\,2\,\)点の変化の割合を求めれば良いことになります。

　\(\,\color{red}{(変化の割合)=\displaystyle \frac{　y\,の増加量　}{　x\,の増加量　}}\,\)

なので
　\(\,(\,x\,の増加量\,)=6-(-6)=12\,\)
　\(\,(\,y\,の増加量\,)=36-(12)=24\,\)

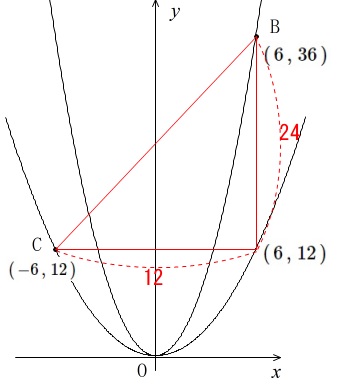
よって変化の割合は

　\(\displaystyle \frac{24}{12}=\,\underline{　2　}\,\)

直線の方程式は求めなくて良いのですよ。

問\(\,3\,\)

座標を文字を使って設定します。
この方法は高校に行っても大切になるのでしっかり復習しておくと良いです。

点\(\,\mathrm{A}\,\)の\(\,x\,\)座標を\(\,t\,\)とおき、
\(\,\mathrm{△ABC}\,\)が直角二等辺三角形になるときの\(\,t\,\)を求めます。

　\(\,\mathrm{A}\,\)と\(\,\mathrm{B}\,\)は\(\,x\,\)座標が同じ
　\(\,\mathrm{A}\,\)と\(\,\mathrm{C}\,\)は\(\,y\,\)座標が同じ

という条件がありますので直下三角形になるのは当然ですが、
　『直角二等辺三角形』
になることがポイントです。

二等辺三角形という一言を見逃すと解けない問題ですよ。

簡単に言うと問題は
　『\(\,\mathrm{AB=AC}\,\)となる\(\,t\,\)を求めなさい。』
ということになります。

　\(\displaystyle \,\mathrm{A}\,\left(\,t\,,\,\frac{1}{3}\,t^2\,\right)\,\)
　\(\,\mathrm{B}\hspace{4pt}(\hspace{4pt}t\,,\hspace{10pt}t^2\,)\,\)
　\(\displaystyle \,\mathrm{C}\,\left(\,-t\,,\,\frac{1}{3}\,t^2\,\right)\,\)

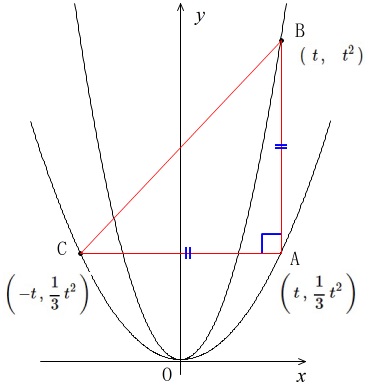
　\(\,\mathrm{AB=AC}\,\)の両辺を\(\,t\,\)を用いて表します。

\(\,\mathrm{AB}\,\)は\(\,x\,\)座標が同じなので\(\,y\,\)座標の差となります。

辺の長さは正なので大きい座標から小さい座標を引いておきます。

　\(\displaystyle \,\mathrm{AB}=t^2-\frac{1}{3}t^2=\color{red}{\frac{2}{3}t^2}\,\)

\(\,\mathrm{AC}\,\)は\(\,y\,\)座標が同じなので\(\,x\,\)座標の差となります。

\(\,\mathrm{AB}\,\)と同じように辺の長さは正なので大きい座標から小さい座標を引いておきます。

　\(\,\mathrm{AC}=t-(-t)=\color{red}{2t}\,\)

よって

　\(\begin{eqnarray}\displaystyle
\color{red}{\frac{2}{3}}\,t^2&=&\color{red}{2\,t}\\
2\,t^2&=&6\,t\\
2\,t^2-6\,t&=&0\\
t^2-3\,t&=&0\\
t\,(\,t-3\,)&=&0\\
t&=&0\,,\,3
\end{eqnarray}\)

\(\,t\,\)は\(\,\mathrm{A}\,\)の\(\,x\,\)座標で正なので\(\,t\,＞\,0\,\)だから

　\(\,t=\underline{　3　}\,\)

条件通りに文字設定して、図示すると分かり易いですよ。

　\(\large{\color{black}{\fbox{　４　}}}\)　（一般入試　\(\color{red}{\fbox{５}}\)　）

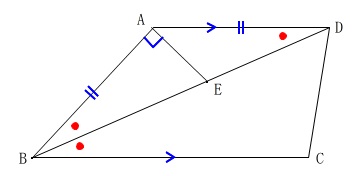
台形の中の角度を求めます。

問題にある条件

　\(\,\mathrm{AB=AD}\,\)
　\(\,\mathrm{AD // BC}\,\)
　\(\,\mathrm{\angle BAE=90°}\,\)

を図の中に書き込むと

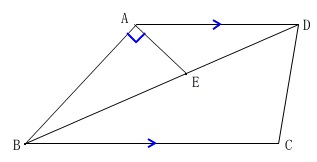
条件
　\(\,\mathrm{AB=AD}\,\)
から二等辺三角形の底角は等しいので
　\(\,\mathrm{\color{red}{\angle ABD=\angle ADB}}\,\)

条件
　\(\,\mathrm{AD　//　BC}\,\)
から平行線の錯角は等しいので
　\(\,\mathrm{\color{red}{\angle ADB=\angle DBC}}\,\)

　
問\(\,１\,\)

角度が具体的な数値で与えられます。

　\(\,\mathrm{\angle ADB=20°}\,\)
　\(\,\mathrm{\angle BCD=100°}\,\)

条件
　\(\,\mathrm{\angle ADB=20°}\,\)
から
　\(\,\mathrm{\angle ABD=\angle ADB=\angle DBC}=20°\,\)

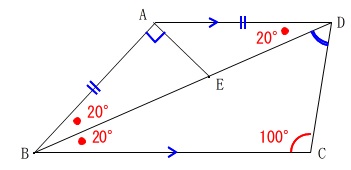
三角形の内角の和が\(\,180°\,\)であることから
　
　\(\begin{eqnarray}
\mathrm{\angle BDC}+\mathrm{\angle DBC}+\mathrm{\angle BCD}&=&180°\\
\mathrm{\angle BDC}+\color{red}{20°}+\color{red}{100°}&=&180°\\
\mathrm{\angle BDC}&=&180-(\color{red}{20°}+\color{red}{100°}）\\
&=&\underline{　60°　}
\end{eqnarray}\)

\(\,\mathrm{\mathrm{AD}　//　\mathrm{BC}}\,\)なので

　\(\,\mathrm{\angle ADC+\angle BCD=180°}\,\)

を使っても同じです。　

問\(\,2\,\)

合同の証明です。

条件は最初の条件に加えて、

　\(\,\mathrm{A}\,\)から\(\,\mathrm{BC}\,\)に垂線を引き\(\,\mathrm{BD,BC}\,\)との交点を\(\,\mathrm{F,G}\,\)
　
このとき、\(\,\mathrm{△ABF　\equiv　△ADE}\,\)　を証明します。
　

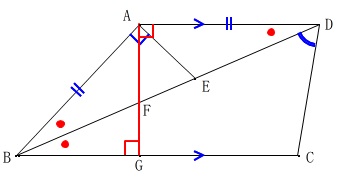
合同でも相似でも証明するときは、図の中で済ませておくことです。

図の中にわかることを書き込んでみると

合同の証明は終わっています。

仮定と、\(\,90°\,\)から共通の角を引いていることを言えば良いのです。

　（証明）
　\(\,\mathrm{△ABF}\,\)　と　\(\,\mathrm{△ADE}\,\)　において
　\(\,\mathrm{AB=AD}　(仮定)　・・・①\,\)
　\(\,\angle \mathrm{ABF}=\angle \mathrm{ADE}　(二等辺三角形の底角)　・・・②\,\)
また
　\(\,\mathrm{AD　//　BC}\,\)
なので\(\,\mathrm{AG}\,\)が\(\,\mathrm{BC}\,\)に引いた垂線であることから
　\(\,\angle \mathrm{AGB}=\angle \mathrm{GAD}=90°\,\)
仮定から\(\,\angle \mathrm{BAE}=90°\,\)なので
　\(\,\angle \mathrm{BAF}=90°-\angle \mathrm{\color{red}{GAE}}\,\)
　\(\,\angle \mathrm{DAE}=90°-\angle \mathrm{\color{red}{GAE}}\,\)
このことから
　\(\,\angle \mathrm{BAF}=\angle \mathrm{DAE}　・・・③\,\)
①②③より
　\(\,1\,\)組の辺とその両端の角がそれぞれ等しい
ので
　\(\,\mathrm{△ABF　\equiv　△ADE}\,\) （終わり）

　裁量問題の　\(\color{black}{\fbox{　3　}}\)　\(\color{black}{\fbox{　4　}}\)
　一般入試問題の　\(\color{red}{\fbox{4}}\)　　\(\color{red}{\fbox{5}}\)
は以上です。

⇒　2019年度北海道公立高校入試裁量問題第5問の解説

裁量問題は　\(\color{black}{\fbox{5}}\)　に続きます。

標準問題はここまでです。

⇒　2019年(平成31年)度北海道公立高校一般入試数学第1問の解説

標準問題の解説はここからです。

⇒　2019年度北海道公立入試裁量問題の解説 第1,2問(一般第2,3)

裁量問題はここからです。

⇒　北海道の公立高校入試数学の過去問と解説

更新はまとめページで確認してください。