円錐(すい)の表面積や側面となる扇形の面積と四角錐や五角錐の体積の求め方の説明です。
体積を求める公式はありますが、公式そのもので求める問題は多くありません。
立体では大切なポイントがありますので錐体の表面積や体積を求める場合でも確認しておきましょう。
円錐（すい）の側面は扇形
円錐は扇形の中心角や弧の長さを含めた問題ができるのでよく出題される立体です。
扇形については平面図形でも説明していますが、再度空間図形のテーマとして取り上げておきます。
空間図形は平面図形の組み合わせでできていると考えれば、平面図形の基礎知識は十分にしておいた方が良いですよ。
問題の中で見ていきましょう。
底面の円の半径が\(\,\mathrm{5\,cm}\,\)、母線の長さが\(\,\mathrm{12\,cm}\,\)の円錐について、次の問に答えなさい。
(1)側面の扇形の中心角を求めなさい。
(2)この円錐の表面積を求めなさい。
『母線』とは円錐の頂点から底面の円周上に引いた線分のことです。
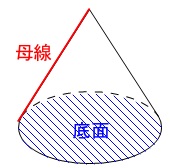なので問題の立体は
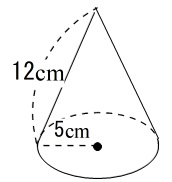となっています。
扇形の中心角の求め方
(1)
円錐（円すい）の問題ですが、立体と考えず平面で考えればただの中心角の問題です。
覚えておかなければならないのは、円すいの展開図のだいたいの形です。
円すいの展開図は「おうぎ形＋円」です。
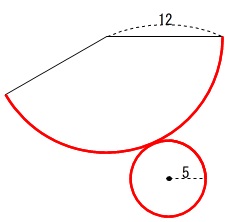
そして、大切なことは、
底面の円周と扇形の弧の長さが等しい
（図の赤線の長さが等しい、）
ということですね。
赤線の長さは円の周なので、
\(2\times\,\pi\times(5)=\color{red}{10\,\pi}\)
弧の長さも同じで \(\,\color{red}{10\,\pi}\,\) となっています。
「おうぎ形の中心角を求めよ。」
なので公式を覚えていれば、
\(\displaystyle 2\times\pi\times 12\times \frac{ 中心角 }{360}=10\,\pi\)
から求めることはできます。
しかし、円を基本に考えるようにしておくと比例式で求めることができます。
半径\(\,12\,\)の円周は\(\,24\,\pi\,\)です。
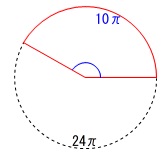
そのうち\(\,10\,\pi\,\)は、
\(\displaystyle \frac{10\,\pi}{24\,\pi}=\frac{5}{12}\)
にあたります。
だから、１周のとき\(\,360^{\circ}\,\)なので、
その\(\,\displaystyle \frac{5}{12}\,\) は、
\(\displaystyle 360^{\circ}\times\frac{5}{12}=\underline{ 150^{\circ} }\)
と求まるのです。
公式化すると、円すいのときの側面のおうぎ形の中心角は、
\(\displaystyle \frac{ \color{blue}{(底面の円の周)} }{\color{red}{(母線)}}\times 360^{\circ}\)
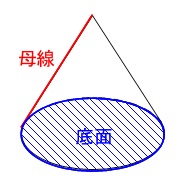
ですが、公式化するより図を書いて考える方を優先した方がいい段階です。
弧の長さと中心角は比例します。
弧の長さの比は \(\displaystyle \frac{10\pi}{24\pi}=\frac{5}{12}\)
なので
中心角の比も \(\displaystyle \frac{5}{12}\)
ということですよ。
\(\,24\pi\,\)で\(\,360°\,\)なら\(\,10\pi\,\)のときの中心角は？
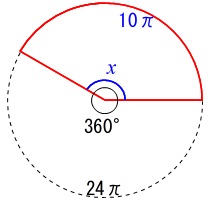
という関係から比例式を立てると、求める中心角を\(\,x\,\)とおいて、
\(\begin{eqnarray}
24\pi:360&=&10\pi:x\\
24\pi\times x&=& 360\times 10\pi\\
x&=&\frac{360\times 10\pi}{24\pi}\\
&=&\frac{360\times 5}{12}\\
&=&150
\end{eqnarray}\)
比例式なので『 \(\,^{\circ}\,\) 』は省いて計算しています。
答えは同じく \(\,\underline{ 150° }\,\)
最初に円を考えて、比例式を立てればすべて同じです。
円錐の表面積の求め方
(2)
円錐の表面積を求めますが、展開図ですね。
円錐の展開図は扇形と円となります。
表面積は、扇形の面積と、底面の円の面積を足すだけです。
扇形の面積は普通に求めれば、中心角が\(\,150°\,\)と分かっているので
\(\hspace{10pt}\displaystyle \pi\times (12)^2\times \frac{150}{360}\\
\displaystyle =\pi\times (12)^2\times\frac{5}{12}\\
=60\,\pi\)
と、求まりますが、扇形の弧の長さがわかっているときは、次の公式が使えます。
\(\,\color{red}{(扇形の面積)=(弧の長さ)\times(扇形の半径)\div 2}\,\)
数学らしく書くと、扇形の面積\(\,\mathrm{S}\,\)は、おうぎ形の半径\(\,r\,\)と弧の長さ\(\,\ell\,\)を用いて、
\(\displaystyle \color{red}{\mathrm{S}=\frac{1}{2}\,r\,\ell} \)
となります。
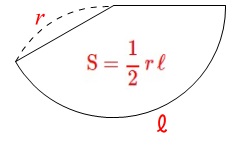
見慣れないうちはわかりにくいでしょうけど 三角形の面積の公式と同じ形をしています。
この公式を使って計算すると扇形の部分の面積は、
\(\begin{eqnarray}\displaystyle
\mathrm{S}&=&\frac{1}{2}\times 12\times 10\,\pi\\
&=&\color{red}{60\,\pi}
\end{eqnarray}\)
とすぐに求まります。
ところで、この扇形は円錐の側面積でもあります。
底面の半径と母線の長さが分かっている円錐の側面積をもめる場合は、
公式があります。
底面の円の半径を\(\,r\,\)、母線を\(\,a\,\)とすると
\(\,(側面積)=a\,r\,\pi\,\)
となりますがおすすめしていません。
側面積に限った公式であることもそうですが、展開図を書くという手順を飛ばしているからです。
もちろん、すべての円錐で成り立つので側面積を出す場合は使って良いですよ。
扇形は平面図形での大きな計算テーマですので復習しておきましょう。
この問題の円錐の表面積を求めましょう。
底面の円の面積は簡単で、半径が\(\,5\,\)の円の面積だから
\(\pi\times (5)^2=\color{red}{25\,\pi}\)
合わせると求める表面積が求まります。
\(\color{red}{60\,\pi}+\color{red}{25\,\pi}=\underline{ 85\,\pi } (cm^2)\)
展開図にすれば、平面で考えることができます。
空間も平面の組み合わせでできているのです。
四角錐や五角錐の体積の求め方
忘れている人が割といるので確認しておきます。
柱体と錐体の体積の求め方です。
\(\,\color{red}{(柱体の体積)=(底面積)\times (高さ)}\,\)
です。
これは、底面の形に関係なく同じです。
三角柱でも四角柱でも円柱でも同じ。
そして、錐体の体積は、
\(\begin{eqnarray}\displaystyle
(錐体の体積)&=&(柱体の体積)\times \color{red}{\frac{1}{3}}\\
&=&\frac{1}{3}\times (底面積)\times (高さ)
\end{eqnarray}\)
です。
これも、底面の形には関係はありません。
三角錐でも四角錐でも円すいでも同じです。
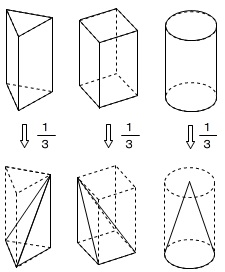
覚えいるけどミスをする人もいます。
錐体の体積を求めるときに\(\,\displaystyle \frac{1}{3}\,\)をかけ忘れたり、
柱体の体積を聞かれているのに\(\,\displaystyle \frac{1}{3}\,\)をかけてしまったり、
という単純なミスです。
問題が何を聞いているかは、問題をよく読んで確認しましょう。
問題です。
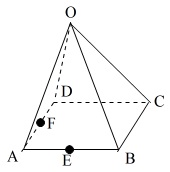
図の\(\,\mathrm{O-ABCD}\,\)は正四角錐で、
底面の正方形の\(\,1\,\)辺が\(\,4\,\mathrm{cm}\,\)、
高さが\(\,6\,\mathrm{㎝}\,\)である。
また，点\(\,\mathrm{E}\,\)，\(\,\mathrm{F}\,\)は、
それぞれ辺\(\,\mathrm{AB}\,\)，\(\,\mathrm{AD}\,\)の中点である。
次の問いに答えなさい。
(1)正四角錐\(\,\mathrm{O-ABCD}\,\)の体積を求めなさい。
(2)五角錐\(\,\mathrm{O-EBCDF}\,\)の体積を求めよ。
(1)
錐体の体積\(\,V\,\)は
\(\displaystyle V=\frac{1}{3}\times (底面積)\times (高さ)\)
です。
高さは問題に書いてあります。
\(\,(高さ)=\color{red}{6}\,\)
底面は正方形で\(\,1\,\)辺が\(\,4\,\)なので
\((底面積)=4\times 4=\,\color{red}{16}\,\)
よって体積\(\,V_{1}\,\)は
\(\begin{eqnarray}\displaystyle
V_{1}&=&\frac{1}{3}\times \color{red}{16}\times \color{red}{6}\\
&=&\underline{ 32 } (\mathrm{cm^3})
\end{eqnarray}\)
この問題では高さが与えられますが、入試レベルになると頂点から底面のどこに垂線が下りるかが問題になることが多いです。
高さ自体を求めることから問題になりますが、三平方の定理（\(\,3\,\)年）を習ってからです。
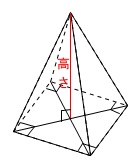
高さは頂点から底面に垂直に下ろした垂線の長さになるので、上の図の赤い線が高さです。
底面が正方形で、正四角錐なので、底面の対角線の交点上に高さとなる垂線は下りてきます。
この問題は高さは与えられているので計算するだけですね。
(2)
五角錐の体積です。
立体はイメージしにくいです。
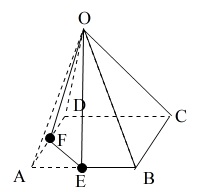
底面は？高さは？
と、ちょっと考えますよね。
コツがありますので、お伝えしておきます。
立体は平面でできています。
だから、
底面は底面を含む面だけを抜き出します。
高さは高さを含む面だけを抜き出します。
底面を五角形だと考えると、五角形の面積を考えなくてはいけません。
五角形（底面だけ）を抜き出すと、
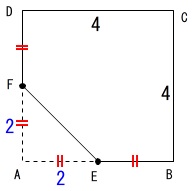
図のようになり、
正方形\(\,\mathrm{ABCD}\,\)から\(\,\mathrm{△AEF}\,\)を切り取れば求まります。
「\(\,\mathrm{E}\,\)，\(\,\mathrm{F}\,\)は中点」
と問題に書いてあるので、\(\,\mathrm{△AEF}\,\)の面積は
\(\displaystyle △\mathrm{AEF}=\frac{1}{2}\times 2\times 2\,=\,\color{blue}{2}\)
正方形\(\,\mathrm{ABCD}\,\)の面積は
\( 4\times 4\,=\color{magenta}{16}\)
なので、底面となる五角形の面積は、
\(\color{magenta}{16}-\color{blue}{2}\,=\color{red}{14}\)
高さは正四角錐\(\,\mathrm{O-ABCD}\,\)と同じ\(\,\color{red}{6}\,\)で変わっていません。
よって、求める体積\(\,V_2\,\)は、
\(\begin{eqnarray}\displaystyle
V_{2}&=&\frac{1}{3}\times 14\times 6\\
&=&\underline{ 28 } (\mathrm{cm^3})
\end{eqnarray}\)
と求まります。
基本的にはこれでいいと思います。
しかし、「全体から一部を引く」というのを覚えておくと良いです。
全体（正四角錐）の体積は、\(\,32\,\mathrm{cm^3}\,\)と求めています。
これから、三角錐\(\,\mathrm{O-AEF}\,\)を引く、という考え方をします。
入試などの応用問題ほどこの、「全体から一部を引く」というのを活用するようになります。
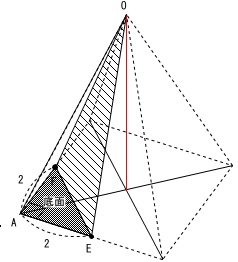底面の\(\,\mathrm{△AEF}\,\)の面積は\(\,\color{blue}{2}\,\)で、
三角錐\(\,\mathrm{O-AEF}\,\)の高さも同じ赤線の\(\,\color{red}{6}\,\)なので、
三角錐\(\,\mathrm{O-AEF}\,\)の体積\(\,V_3\,\)は、
\(\begin{eqnarray}\displaystyle
V_3&=&\frac{1}{3}\times \color{blue}{2} \times \color{red}{6}\\
&=&4
\end{eqnarray}\)
よって求める体積は、全体から三角錐\(\,\mathrm{O-AEF}\,\)を引いて
\(32-4=\underline{ 28 } (\mathrm{cm^3})\)
体積の問題は、「難しい」と感じたら、「全体から部分を引く」と思い出して下さい。
きっと役に立つときが来ます。
問題だけを見ていってもわかりますが、同じ方法で面積や体積を求める応用問題が全国的によく出題されています。
大きな差となるところですよ。
クラブ活動で忙しい！
塾に通っているのに数学が苦手！
数学の勉強時間を減らしたい！
数学の勉強方法が分からない！
その悩み、『覚え太郎』が解決します！！！
