扇(おうぎ)形の面積を求める公式と弧の長さの求め方

扇（おうぎ）形の面積を求める公式3つと弧の長さの求め方をお伝えします。
面積と弧の長さは比例ですべて解けるのですがこれを苦手にしている中学生はものすごく多いです。
これには当然とも言える理由が３つあります。
ここで図形を苦手にしたくないならやっておくべき作業の確認をしておくと逆に図形で強くなれますよ。

なぜ中学生が扇形を苦手にするか？

中学生だけならまだ良いですが、扇形の面積を求められない高校生にも良く出会います。

これには理由がはっきりとあるのですが、わかりますか？

これらの理由が混じって、とことん難しく感じさせているのです。

あなたが悪いのではありません。
学校や塾では普通に教科書通りの教え方をするので、しかたないことです。

しかし、
わからないといっているヒマはありません。

立体で、円錐の表面積などでも扇形の面積は求められなくてはなりません。

ここを放っておくとあとあと苦手なものが増えていきます。
今からでも遅くないので求められるようにしておきましょう。

円の面積と周の長さの公式

これは覚えておくしかありません。
中学生には導くことができないのです。

ただ、これは小学校の時の算数で、
　円周の長さは、『直径×\(\,3.14\,\)』
　円の面積は、『半径×半径×\(\,3.14\,\)』
と覚えさせられたはずです。

これに
　\(\color{red}{ 半径を　r}　\)
として公式としたものなのでなんとしても覚えましょう。

　\(　3.14　は円周率　\pi　です。\)

となりますので文字として覚えましょう。

ちょっと細かいことを言うと、

　直径×\(\,3.14\,\)
を文字にすると
　\(2r\pi\)

という順序になりますが、覚えられるならどちらでも良いですよ。

公式（文字式）としては、
　\(\large{\color{red}{ \pi　は定数なので先に来る}}\)
というだけですから。

この２つの公式で扇形の面積がすぐに出るわけではありませんが、
この値が基本になって、次の段階に進めるのです。

つまり、この段階がクリアーできないと扇形の問題は解けません。

おうぎ形の面積の公式と求め方

教科書には扇形の面積や弧の長さを求める公式があります。

となります。

参考書や問題集もだいたいこの公式を使います。

よく見かける公式としてはもう2つあります。

扇形の弧の長さを\(\,\ell\,\)とし、半径を\(\,r\,\)とすると面積\(\,S\,\)は

　\(\,\displaystyle\color{red}{ \large{S=\frac{1}{2}\,\ell\,r}}\,\)

といった公式や、
円すいの底面の半径\(\,r\,\)と母線\(\,\ell\,\)が分かっているとき、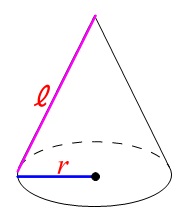
この円すいの側面積\(\,S\,\)は

　\(\color{red}{\large{S=\ell\,r\,\pi}}\)

などといった公式もあります。
私も一つ目は覚えるようにいっていますが、
まずは比例式で中心角が出せることが先です。

何故二つ目は覚えるようにいわないか？
覚えて、使って良いですよ。

ただし、2つの目の公式は扇形の面積ですが『側面積』です。
表面積を聞かれることの方が多いので、
公式で側面積を出す前にやることがあるから必要無いとしています。

『覚え太郎』会員は意味のない使い方はしないようにして下さい。

確かにどれも覚えた方がはやいです。
問題を作るときに、円錐などの問題にすれば、扇形についても含めることができるので、入試にも良く出題されます。

時間をかける問題でも無いので、
　公式に値（半径の値か中心角）を代入して、
サクッと求めておくと少しは時間に余裕が持てますから、覚えて使えるようになるまで練習を繰り返しておくといいでしょう。

しかし、

　\(\color{red}{　\displaystyle \ell=2\pi r \times \frac{a}{360}\\
　\displaystyle S=\pi r^2 \times \frac{a}{360}}\)

この公式は計算が二段階になっているんです。
『円の公式＋扇形の中心角をかける』
という二段階の計算を含んでいるということです。

円の公式を覚えていないのにこれを覚えようとしている時点で無理があります。
学校や当会以外の塾では「円の公式は覚えているもの」として進めているので、
まずは円の公式をしっかりと覚えてからにしましょうね。

ただ、この公式は覚えなくてもいいです。
円の公式は覚えないと使えませんよ。値も求められません。

でも、扇形については公式は必要ありません。

次の３つめの理由にもつながりますが、
自分でちょっとした作業をすることで公式はいらなくなります。

事実、公式よりこちらで覚えた中学生の方があとあと伸びる傾向にあります。

数学の大切な基本作業が身についていくからです。

図形が苦手な人が多い理由

『扇形』って書いてる時点で、『図形問題』だとわかりますよね？

それなのに図を書かずに計算している中学生が多いです。
これが図形を苦手にする３つめの理由です。

メンドクサイかもしれませんが図は書きましょう。
自分のためです。

簡単な例題で見てみましょう。

この問題は図形の問題です。簡単にで良いので図を書きましょう。

基本（基準）となるのは円です。

円の中心角は　\(\,360^\circ\,\)　なのでこれを基本とします。

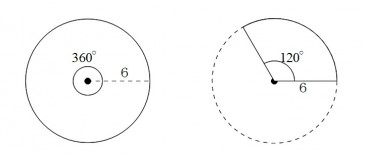
実際には右の図１つで大丈夫です。

ここで使うのが、１年のずっと前にならっている比例式です。

扇形の弧は中心角に比例します。面積も同じです。

どういうことかと言うと、
　中心角が２倍になれば、弧や面積も２倍になるということ。
　逆に中心角が半分になれば、弧や面積も半分になる、
ということですね。

比例式で思い出して欲しいのが、
『内項の積』＝『外項の積』
という関係式です。

文字で表すと、

　\(『　\color{red}{ a\,:\,b\,=\,c\,:\,d　なら　 bc\,=\,ad }　』\)

これは思い出しておいて下さいよ。

⇒　1次方程式と比例式の利用と解き方のまとめ

では、問題に戻ります。

　半径が\(\,6\,\)の円周は\(\,12\pi\,\)です。
（ \(\,2\pi\,r\,\)の\(\,r\,\)に\(\,6\,\)を入れる）

これが
　中心角　\(\,360^\circ\,\)　のときの弧の長さ
と言えます。

では中心角　\(\,120^\circ\,\)　のときは？

これを比例式にするのです。

　求めたい弧の長さを　\(\,x\,\)　としましょう。
（文字は\(\,\mathrm{A}\,\)でも何でも良いです。）
すると、

　\(「　360^\circ　のとき　12\pi \\
　120^\circ　のとき　x 」\)

という比例式ができるので、

　\( 360:12\pi=120:x\)

または

　\( 360:120=12\pi:x\)

\(　360^\circ　や　120^\circ　の\\
『　a^{\color{red}{ \circ}} 』\)
\(\,\color{red}{○}\,\)（赤丸）はなくて良いです。
比例式だからいらない。

後は、
『 内項の積 』＝『 外項の積 』を利用して、
\(\,x\,\)について方程式を解けば良いだけです。

　答えは　\(\underline{\,4\pi\,}\)　です。

この方程式を解くのは自分でやって見てください。
これは参考書や問題集を上手く利用出来ない理由の１つでもあります。
そもそも問題集や参考書の解説が分かりにくい、
それもありますが、
人の計算を見て自分でやった気になっているのも上手く利用出来ない理由ですよ。

　\( 360\times x=12\pi \times 120\)

だから

　\( x=\displaystyle \frac{12\pi \times 120}{360}=4\pi\)

⇒　比例式の応用 文章題への利用と便利な比の使い方

比例関係の使い方がうまくなれば、
　\(\displaystyle 12\pi \times \frac{120}{360}=4\pi\)
と直接出せるようになります。

まとめ

長くなってしましいましたが、公式が使いこなせず扇形の問題が苦手な人は、理由を１つひとつつぶして、扇形を克服してください。

立体になっても使えますから大きな効果があります。
比例式は３年生の大注目単元『相似』でも大活躍しますよ。

今から慣れておくと良いですね。

　⇒　中学1年の平面図形のポイントと空間図形とのつながり

平面図形のポイントと重要性は知っておきましょう。

クラブ活動で忙しい！
塾に通っているのに数学が苦手！
数学の勉強時間を減らしたい！
数学の勉強方法が分からない！

その悩み、『覚え太郎』が解決します！！！