表面積や体積の求め方(三角柱,四角柱,円柱,球や半球)

表面積や体積の求め方のポイントです。
代表的な三角柱,四角柱,円柱,球や半球などを取り上げて説明しますが、公式ではなく、求めるための手順を覚えるようにしましょう。
問題には公式が使えない立体が多く出てきますので、覚えることを間違えないようにしてください。

三角柱の体積と表面積の求め方

三角柱や四角柱や円柱はまとめて柱体といいます。

柱体の体積\(\,V\,\)は

　\(\color{red}{V=(底面積)\times (高さ)}\)

で求まるので体積が求められないという人は少ないです。

この計算公式は、底面の形に関係なく（円柱も三角柱も四角柱も全部）成り立ちます。

しかし、表面積は少しややこしくなるので、展開図をしっかり書くことです。
ここが重要なポイントです。

『覚え太郎』にも入れてありますが、

　問題に『表面積』とあれば『展開図を書く』

という基本作業は忘れないようにしましょう。

⇒　中学数学を短期攻略する『覚え太郎』

表面積は展開図を書いて、部分部分の面積を求めて足します。
だから、展開図無くして表面積は求まらない、と考えておいて下さい。

なれてくると簡単な図形の表面積なら展開図なしでも求められるようになります。

しかし、
公立高校入試や実力テストでもしっかり点数を取りたいなら、
展開図は慣れて来ても書くようにした方が良いですよ。

問題を解いてみましょう。

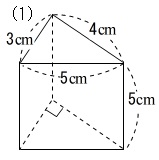
展開図から書いてみましょう。
コツは、「横の面を長方形にしてしまう」ということです。

展開図を書いてみると、

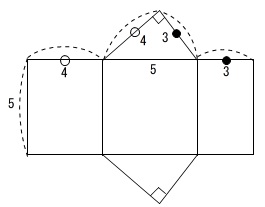
上の図のようになります。

展開図の上の直角三角形と下の直角三角形は同じです。
※
三平方の定理を知っていれば直角が書いてなくても直角三角形と分かりますが、ここでは直角を示してあります。

長方形の面積は区切りがありますが１つひとつ出さなくても、
１つの長方形として求めれば良いんですよ。

上下の三角形の面積は直角三角形なので、１つの面積が
　\(\displaystyle \frac{1}{2}\times 3\times 4=6\)
　
２つ分あるで、

　\(6\times 2=\color{red}{12}\)

長方形の部分は,

　横が　\(\,4+5+3=\color{blue}{12}\,\)

　高さが　\(\,\color{magenta}{5}\,\)

なので、長方形の面積は
　
　\(\color{blue}{12}\times \color{magenta}{5}=\color{red}{60}\)

合わせると

　\(\color{red}{12}+\color{red}{60}=\underline{　72　}　(\mathrm{cm^2})\)　

体積は簡単で、底面積がさっきの直角三角形なので\(\,\color{red}{6}\,\)とわかっています。

柱体の体積\(\,V\,\)は

　\(\color{red}{V=(底面積)\times (高さ)}\)

高さの\(\,\color{magenta}{5}\,\)をかけて、

　\(\,V=\color{red}{6}\times \color{magenta}{5}=\underline{　30　}　(\mathrm{cm^3})\,\)

と出てきます。

四角柱の体積と表面積の求め方

次は四角柱ですが、柱体はどれも同じ方針で進めてかまいません。

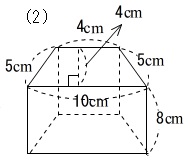
表面積を求めるために展開図を書きます。

そのとき、横にある面（側面）を長方形として横に広げて書きます。

上下の面（底面）はその長方形にひっつけてしまえば良いだけです。
※
柱体は上の面と下の面は合同になります。
どちらの面も『底面』というので覚えておきましょう。

どこでもひっつければ良いのではなくて、長さの等しいところはつなげるように書きます。

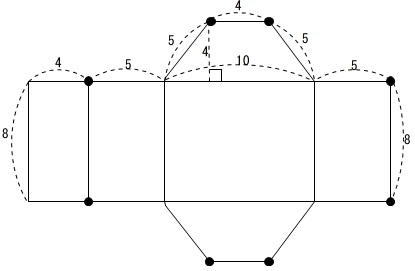
この展開図さえかければ、必ず計算できます。
長方形と台形の組み合わせです。

組み立てると、・が重なります。
台形は上と下は同じ形で大きさも同じです（合同）。
※
合同という用語は中学\(\,2\,\)年以降良く使うようになります。

この展開図さえ書ければ、小学校の面積問題です。
キーワードは「表面積」とあれば、・・・。

『覚え太郎』を何度も見て、考えなくて良いようにしておきましょう。

さて、計算しておきましょう。

上下の台形は、それぞれ１つが、

　\(\displaystyle \frac{1}{2}\times (4+10)\times 4=\color{blue}{28}\)

です。

小学校のときに習った公式を覚えてますよね？

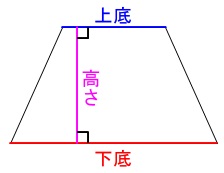
　\((台形の面積)=(\color{blue}{上底}＋\color{red}{下底})\times (\color{magenta}{高さ})\div 2\)

台形は２つあるので、上下合わせると、

　\(\color{blue}{28}\times 2=\color{red}{56}\)

長方形の面積は、高さが\(\,\color{magenta}{8}\,\)なので

　\(\hspace{10pt}(4+5+10+5)\times \color{magenta}{8}\\
=24\times 8\\
=\color{red}{192}\)

台形2つ分と合わせて表面積は、

　\(\color{red}{56}+\color{red}{192}=\underline{　248　}　(\mathrm{cm^2})\)

体積は、
　底面積が台形の面積\(\,\color{blue}{28}\,\)
なので、
　高さの\(\,\color{magenta}{8}\,\)をかけて、

　\(\begin{eqnarray}
V&=&\color{blue}{28}\times \color{magenta}{8}
&=&\underline{　224　}　(\mathrm{cm^3})
\end{eqnarray}\)

方針が決まっていれば考えることはそれほどありません。

方針を決めずにあれこれ考えるのは時間がかかります。
考えるのが良くないと言っているのではありませんが、考えてもろくなものは出てきません。笑

方針、つまり、問題を解くときの方法や作業はいろいろとあります。
しかし、試験中に急に思いつくということはほとんどありません。

答えを合わせるためだけに計算をひたすらやって、
時間をかけて勉強しているように見せていても数学の得点は伸びません。

どれだけ方針を決めておけるか、何がポイントになるのかを知っておくことが大切なのです。

試験を受ける前にすでに得点は決まっていると言ってもいいくらいです。

円柱の体積と表面積の求め方

円柱でも方針は同じです。
公式が使える体積は公式通りに必要な値を求めます。

表面積は公式がない場合が多いので『展開図』です。
※
展開図が書けない球は後で説明します。

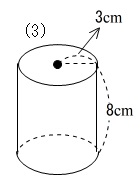
これも柱体なので(1)(2)と同じです。

展開したとき側面が長方形だと覚えておけば、展開図は楽に書けます。

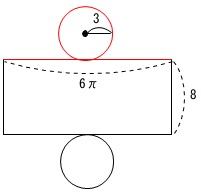
図の赤い円の周の長さと、長方形の横の長さが等しいことに注意してください。

円の周の長さは、半径を\(\,\color{blue}{r}\,\)とすると

　\(\begin{eqnarray}
(円周)&=&(\color{magenta}{直径}) \times (\color{red}{円周率})\\
&=&(2\,\times \color{blue}{r}\,) \times \color{red}{\pi}\\
&=&2\,\pi\,r
\end{eqnarray}\)

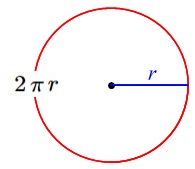
なので、（円周率は\(\,\color{red}{\pi}\,\)と表します）
長方形の横の長さは、
　\(2\times 3\times \pi=\color{red}{6\pi}\)

円の面積は、
　\(\begin{eqnarray}
(面積)&=&(\color{blue}{半径})\times (\color{blue}{半径})\times (\color{red}{円周率})\\
&=&\color{blue}{r}\times \color{blue}{r}\times \color{red}{\pi}\\
&=&\pi\,r^2
\end{eqnarray}\)

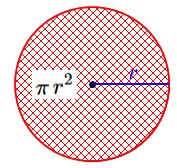
なので、円の面積1つ分は、

　\(\pi\times\,(3)^2=\color{red}{9\,\pi}\)

となります。　

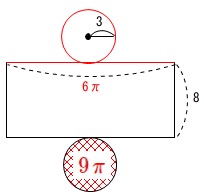
側面の長方形の面積は、

　\(6\pi\times 8=\color{red}{48\,\pi}\)

なので、求める表面積は底面2つと合わせて、

　\(\begin{eqnarray}
　(表面積)&=&\color{red}{9\,\pi} \times 2+\color{red}{48\,\pi}\\
&=&18\,\pi+48\,\pi\\
&=&\underline{　66\,\pi　}　(\mathrm{cm^2})\end{eqnarray}\)

体積\(\,V\,\)は、
　底面積が円の面積で\(\,\color{blue}{9\,\pi}\,\)
　高さが\(\,\color{magenta}{8}\,\)
だから、

　\(\begin{eqnarray}
V&=&\color{blue}{9\,\pi}\times \color{magenta}{8}\\
&=&\underline{　72\,\pi　}　(\mathrm{cm^3})
\end{eqnarray}\)

公式が使えないのは、体積より表面積です。
「表面積」とあれば「展開図」、忘れずにいればどれも同じ問題に見えてきますよ。

球（半球）の体積と表面積の求め方

表面積と言われても展開図が書けないのはこの球です。

球だけは公式を使わないと表面積、体積とも中学生は求められません。
※
高校生でも公式を使わないと求められない人はたくさんいます。

⇒　中学1年の空間図形問題の考え方ポイントと覚えておく公式

確認しておくと良いです。

ここでも書いておきます。

球の半径を\(\,r\,\)とすると
　\(\displaystyle \color{red}{(体積)=\frac{4}{3}\,\pi\,r^3}\)
　\(\color{red}{(表面積)=4\,\pi\,r^2}\)
です。

必ず覚えておきましょう。

公式は導けないと意味がないという人がいますが、無視しておくように。
公式は使えることが先で良いです。

球が出てくると空間図形の問題はかなり難しくなることがあります。　
大学入試でも球を苦手にしている人は多いです。笑

しかし、公式を使えるかどうかが基本なので必ず覚えておきましょう。
中学校の数学の場合は体積と表面積の公式になります。

分かり易い体積から求めておきます。

半径\(\,6\,\)の球の体積は

　\(\displaystyle \frac{4}{3}\times \pi\,\times (6)^3\)

なので半球の体積は

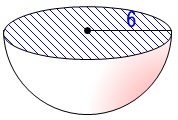
　\(\hspace{10pt}\displaystyle \frac{1}{2}\times \frac{4}{3}\times \pi\,\times (6)^3\\
\displaystyle =4\times \,\pi\,\times 6^2\\
=\color{red}{144\,\pi}\)

くり抜く直方体の体積は

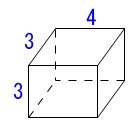
　\(3\times 4\times 3=\color{red}{36}\)

よって求める体積\(\,V\,\)は

　\(\,V=\underline{　144\,\pi-36　}　(cm^3)\,\)

体積や面積を求めるとき、公式が通用しないときは
　『部分』＋『部分』
　『全体』－『部分』
を利用することはよくあります。

これはその典型です。

表面積は簡単には求まりませんが、部分部分は難しくはありません。

まずは半球の表面部分、

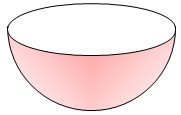
展開図は書けないけど球の表面積の半分なので公式で求まります。

　\(\displaystyle 4\,\pi\times (6)^2\times \frac{1}{2}=\color{red}{72\,\pi}\)

次に上面を抜き出すと

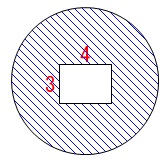
円から長方形が欠けています。

円の面積は
　\(\pi\times(6)^2=36\,\pi\)
長方形の面積は
　\(4\times 3=12\)
だから上面の面積は
　\(\color{red}{36\,\pi-12}\)

直方体の下の面も足せば円になるので、後は直方体の側面積だけを足せば表面積は出ます。
しかし、ここでは部分部分を出しておきます。

半球の中の面、これは直方体の表面積から上面の長方形を引いたもので、

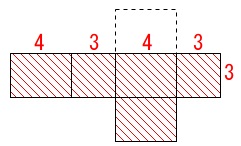
展開図を書いた方が確実ですので、簡単に書いて見てください。

展開図の下にある長方形が先ほど円からくり抜いた長方形なのでこれを、
くり抜いた部分に当てはめれば、側面積だけを足すなら円のままで良いことが分かります。

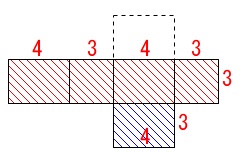
展開図の面積は
　\(\hspace{10pt}(4+3+4+3)\times 3+4\times 3\\
=14\times 3+12\\
=42+12\\
=\color{red}{54}\)

よって求める表面積は

　\(\hspace{10pt}\color{red}{72\,\pi}+\color{red}{36\,\pi-12}+\color{red}{54}\\
=\underline{　108\,\pi+42　}\)

高校入試の場合はほとんどに単位がつきますが、問題に単位がないときは単位は必要ありません。

空間の問題に取り組むときの大切なポイントですが、立体のまま考えない、ということです。
１つひとつ面を取りだして考えていきましょう。

展開図もその1つですよ。

ただし、球は公式利用しかできません。

柱体が終われば次は錐体（すい体）です。

⇒　円錐(すい)の表面積や四角錐,五角錐の体積の求め方

円すいについては扇形の面積が求まられなければ始まりません。

⇒　扇(おうぎ)形の面積を求める公式と弧の長さの求め方

復習しておくと良いですよ。