1次関数との交点の座標の求め方と、グラフから読み取り直線の方程式を求める方法です。
ここでは一次関数に限定して直線と直線の交点を求める問題を取り上げて説明します。
交点を求める問題は1次関数だけでなく高校の数学でも必ず必要になりますが、考え方はすべて同じです。
一次関数を表すグラフの書き方
関数のグラフの書き方を説明していませんでしたが、
どのような関数でもグラフを書くときの基本は、
関数を満たす点をたくさん取ってつなぐことです。
もともと関数のグラフは、その関数を満たす点を無数に集めてできています。
ただ、グラフの形が決まっているときはおおよよの形が分かっているので少ない座標でもグラフがかけるというだけですよ。
できるだけ簡単に、短時間でかきたいですからね。
どういう形をしているかを覚えておけば少ない情報でもグラフがかけます。
\(\,1\,\)次関数の場合は直線になると分かっているので、
異なる\(\,2\,\)点をとって直線としてつなげばグラフはできあがります。
例えば、\(\,(\,-2\,,\,2\,)\,\)、\(\,(\,3\,,\,7\,)\,\)を通る直線は、
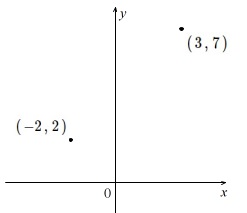 \(\,2\,\)点の座標を点として書き込み、直線としてつなぐだけです。
\(\,2\,\)点の座標を点として書き込み、直線としてつなぐだけです。
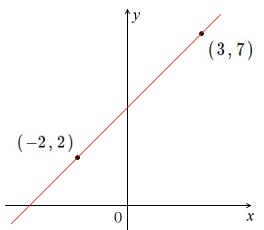
グラフの書き方はたくさん点を取ってつなぐことですが、
直線、\(\,1\,\)次関数においては\(\,2\,\)点を探してつなぐことでグラフがかけます。
これは文章題で大切なポイントになるので覚えておきましょう。
文章題でもグラフを利用して解く問題があります。
苦手にしている人が多いですが、グラフを書くという基本的なことをしないから難しく感じるのです。
『電車やバスの往復』、『兄と弟が時間差で出発する』問題などでもそれぞれのグラフを書けば同じ\(\,1\,\)次関数の問題ですよ。
グラフを読み取り直線の式を求める方法
先にグラフの読み取りをやっておきましょう。
問題3
図について次の問に答えなさい。
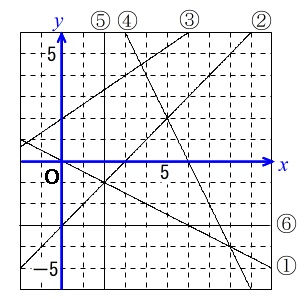 (1) ①~⑥の直線の式を求めなさい。
(1) ①~⑥の直線の式を求めなさい。
(2)連立方程式
\( \begin{cases}
\hspace{7pt} y=x-3\\
\hspace{7pt} 2x+y=12
\end{cases}\)
の解を図を利用して求めなさい。
(3) 直線③と④の交点の座標を求めなさい。
(1)
グラフから直線の方程式を求めるときは、切片から求まることが多いです。
例えば、①の直線は\(\,y\,\)軸と原点の位置で交わっているので、
切片\(\,b\,\)は\(\,0\,\)
と分かります。
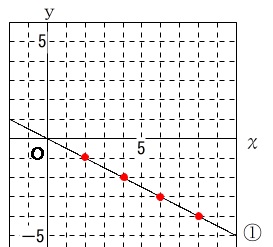 切片が\(\,0\,\)と分かれば求める直線は
切片が\(\,0\,\)と分かれば求める直線は
\(\,y=ax\,\)
とおけて、図から
\(\,(\,2\,,\,-1\,)\,\)を通っている
のが見て取れるので、
代入すると、
\(\begin{eqnarray}\displaystyle
(-1)&=&a\times (2)\\
-1&=&2a\\
2a&=&-1\\
a&=&-\frac{1}{2}
\end{eqnarray}\)
と求まるので答えは
\(\displaystyle \,\underline{ y=\frac{1}{2}x }\,\)
通っている点は、
\(\,(\,2\,,\,-1\,)\,\)
\(\,(\,4\,,\,-2\,)\,\)
\(\,(\,6\,,\,-3\,)\,\)
などもあります。
\(\,x,y\,\)がともにきれいに読み取れる整数だと分かる点(格子点)ならどれでも良いですよ。
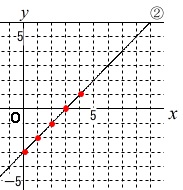
②は\(\,y\,\)軸との交点が\(\,-3\,\)なので
切片が\(\,-3\,\)
と分かります。
 だから求める直線の式は
だから求める直線の式は
\(y=ax\color{red}{-3}\)
とおけて、これが
点 \(\,(\,2\,,\,-1\,)\,\)
を通っているので、\(y=ax-3\,\)に代入して、
\(\begin{eqnarray}
(-1)&=&a\times (2)-3\\
-1&=&2a-3\\
2a-3&=&-1\\
2a&=&-1+3\\
2a&=&2\\
a&=&1
\end{eqnarray}\)
よって答えは \(\,\underline{ y=x-3 }\,\)
これも通る点の選び方はたくさんあります。
\((\,5\,,\,2\,)\)でも\(\,(\,3\,,\,0\,)\,\)でもはっきり読み取れる点ならどれでも良いです。
③も\(\,y\,\)軸との交点が分かります。
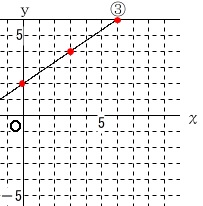 切片は\(\,\color{red}{2}\,\)です。
切片は\(\,\color{red}{2}\,\)です。
なので求める直線は
\(\,y=ax\color{red}{+2}\,\)
とおけて、これが\(\,(\,3\,,\,4\,)\,\)を通るので\(\,y=ax+2\,\)に代入します。
\(\begin{eqnarray}\displaystyle
(4)&=&a\times (3)+2\\
4&=&3a+2\\
3a+2&=&4\\
3a&=&4-2\\
&=&2\\
a&=&\frac{2}{3}
\end{eqnarray}\)
よって求める直線③は \(\displaystyle \,\underline{ y=\frac{2}{3}x+2 }\,\)
2点を通る直線の求め方
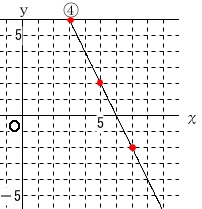
④
これは切片の位置が見えないところにあるので、
 \(\,2\,\)点の変化の割合から傾きだけを先に求めてもいいし、
\(\,2\,\)点の変化の割合から傾きだけを先に求めてもいいし、
連立方程式を解いても良いです。
しかし、
\(\,2\,\)点を通る直線は、後でもいろいろと使えるので、
すべてこちらで説明した方法で求めておくことにします。
※
理由の一部も説明していますので確認しておいてください。
図から\(\,(\,4\,,\,4\,)\,\)と\(\,(\,5\,,\,2\,)\,\)
の\(\,2\,\)点を通るので
\(\,(\,\color{red}{4}\,,\,\color{blue}{4}\,)\,\)
\(\,(\,\color{red}{5}\,,\,\color{blue}{2}\,)\,\)
\(\,x,y\,\)の増加量を求めるときはどちらとも下の座標から上の座標を引きます。
\(\,x\,の増加量=(\color{red}{5})-(\color{red}{4})=1\,\)
\(\,y\,の増加量=(\color{blue}{2})-(\color{blue}{4})=-2\,\)
このとき
\(\displaystyle \,傾き\,\color{red}{a}\,=\frac{-2}{1}=\color{red}{-2}\,\)
これから求める直線は
\(y=\color{red}{-2}x+\color{blue}{b}\)
とおけて、どっちか\(\,1\,\)点を代入すれば切片\(\,\color{blue}{b}\,\)が求まります。
\(\,(\,4\,,\,4\,)\,\)を代入してみましょう。
\(\begin{eqnarray}
(4)&=&-2\times (4)+\color{blue}{b}\\
4&=&-8+\color{blue}{b}\\
-8+\color{blue}{b}&=&4\\
\color{blue}{b}&=&4+8\\
\color{blue}{b}&=&\color{blue}{12}
\end{eqnarray}\)
よって答え \(\,\underline{ y=-2x+12 }\,\)
\(\,(\,5\,,\,2\,)\,\)を代入して成り立たなければ計算ミスしていますよ。
⑤は直線ですが\(\,1\,\)次関数ではありません。
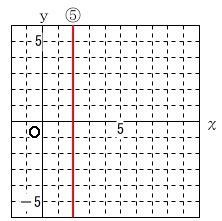 \(\,y\,\)の値に関係なく\(\,x\,\)は\(\,2\,\)です。
\(\,y\,\)の値に関係なく\(\,x\,\)は\(\,2\,\)です。
この直線は\(\,y\,\)軸に平行な直線で傾きとなる数値がありません。
直線の式は \(\,\underline{ x=2 }\,\)
直線だけど一次関数にならない1つです。
直線だけど一次関数にならないもう一つが⑥です。
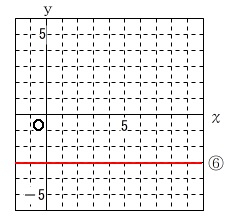 この直線は\(\,x\,\)の値に関係なく、\(\,y\,\)がつねに\(\,-3\,\)です。
この直線は\(\,x\,\)の値に関係なく、\(\,y\,\)がつねに\(\,-3\,\)です。
この直線の方程式は \(\,\underline{ y=-3 }\,\)
この直線は傾きがないわけではなく、傾きが\(\,0\,\)なのです。
そのため一次関数になりません。
直線だけど\(\,1\,\)次関数にならない
この2つは忘れないようにしておきましょう。
2直線の交点の求め方
2直線の交点を求める方法を2つ問題にしています。
直感的にグラフから読み取る方法と
確実に関数の共有点を求める方法です。
交点をグラフから読み取る方法
(2)
『連立方程式
\( \begin{cases}
\hspace{7pt} y=x-3\\
\hspace{7pt} 2x+y=12
\end{cases}\)
の解を図を利用して求めなさい。』
ですが、この問題は無視していいです。
図を利用した交点は、\(\,x\,\)も\(\,y\,\)も整数の場合以外、いいかげんな交点しか出てきません。
定期テストで出されるか、入試でも交点を直感的に読み取る問題はあるので取り上げていますが、
\(\,x\,\)も\(\,y\,\)もきれいに整数で交わる場合しかありません。
時間がなくて勘で答えるならグラフの読み取りでも別にかまいませんけど。笑
ただ、理解しておいて欲しいのは「交点」ということは、
\(\,x\,\)座標も\(\,y\,\)座標も両方の関数に共通である
ということです。
つまり、連立方程式を解けば正確な座標が求められるということです。
この問題の2つの直線の方程式は
\(\,y=x-3 ・・・②\,\)
と、もう一つは
\(\begin{eqnarray}
2x+y&=&12\\
y&=&-2x+12 ・・・④
\end{eqnarray}\)
なので図の②と④を示していることが分かります。
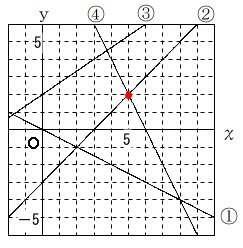 だから交点の座標は、図から読み取れるのは、
だから交点の座標は、図から読み取れるのは、
\(\underline{ x=5\,,\,y=2 }\)
これが答えです。
ただし、2つの関数の交点はいつも整数で答えが出てくるとは限りません。
だから、どんな場合でも「交点」とあれば「連立方程式を解く」ようにしておくと間違いありません。
答えは同じです。
連立方程式は自分で解いて確認してください。
連立方程式を先に学ぶのは交点を求めるためでもあるのです。
連立方程式で一次関数の交点を求める方法
(3)
『直線③と④の交点の座標を求めなさい。』
これは③と④の連立方程式を解けば良いということです。
③は
\(\displaystyle \,y=\frac{2}{3}x+2\,\)
④は
\(\,y=-2x+12\,\)
なのでこれを連立させると、
左辺が両方\(\,y\,\)で同じなので、右辺どうしも等しいということになります。
\(\begin{eqnarray}\displaystyle
\frac{2}{3}x+2&=&-2x+12\\
2x\color{red}{+6}&=&\color{blue}{-6x}+36\\
2x\color{blue}{+6x}&=&36\color{red}{-6}\\
8x&=&30\\
x&=&\frac{30}{8}\\
&=&\frac{15}{4}
\end{eqnarray}\)
この値を③または④に代入すれば\(\,y\,\)が求まります。
どっちに入れても同じ値が出てこなければ計算ミスしています。
どちらでも良いですが計算が楽に思える方に入れたら後は迷うことなく計算に集中します。
④に入れた方が少し計算が楽か、と思えたので④に代入します。
\(\begin{eqnarray}\displaystyle
y&=&-2\times \left(\frac{15}{4}\right)+12\\
&=&-\frac{15}{2}+12\\
&=&\frac{-15+12\times 2}{2}\\
&=&\frac{-15+24}{2}\\
&=&\frac{9}{2}
\end{eqnarray}\)
③に代入してみます。
\(\begin{eqnarray}\displaystyle
y&=&\frac{2}{3}\times \left(\frac{15}{4}\right)+2\\
&=&\frac{5}{2}+2\\
&=&\frac{5+2\times 2}{2}\\
&=&\frac{5+4}{2}\\
&=&\frac{9}{2}
\end{eqnarray}\)
約分をうまく使えば同じようなものですね。
求める交点の座標は、
\(\displaystyle \underline{ \left(\,\frac{15}{4}\,,\,\frac{9}{2}\,\right) }\)
 おおよその数値で良いの座標が位置が一致しているか確認しておくと計算ミスの確認ができます。
おおよその数値で良いの座標が位置が一致しているか確認しておくと計算ミスの確認ができます。
高校の数学でも
\(\,\color{red}{「交点」 \Leftrightarrow 「連立方程式」}\,\)
ですよ。
関数問題で交点の座標を求めることがない、
ということは「ほぼ」ありません。
連立方程式は関数でも文章題でも使いますよ。
次は直線で三角形の面積を二等分してみましょう。
入試でも応用としてよく取り上げられる問題です。
