変化の割合とは？1次関数の求め方と直線の方程式との違い

変化の割合とは１次関数では傾きと同じことですが、１次関数だけで使う言葉ではありません。
また、一次関数を求めることと直線の方程式を求めることも同じに見えて違うところもあります。
入試でもよく出てくる言葉なのでここで確認して、しっかり区別できるようにしておきましょう。

変化の割合とは？

変化の割合とは、\(\,y\,\)が\(\,x\,\)の関数で表されるときに、
関数上の\(\,2\,\)点の間で
　\(\,x\,\)の増加量が\(\,\color{red}{a}\,\)
　\(\,y\,\)の増加量が\(\,\color{blue}{b}\,\)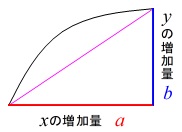
のときに、
　\(\hspace{4pt}\displaystyle \,(\color{magenta}{変化の割合})=\frac{　\color{blue}{b}　}{　\color{red}{a}　}\,\)
のことをいいます。
関数が途中で増えたり減ったりしても関係なく、
平均的な値となるので『平均変化率』ともいますが
高校に進学してから使ってください。

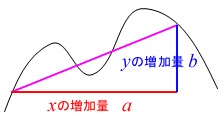
\(\,x\,\)は小さい方から大きい方に見れば、
（大きい\(\,x\,\)から小さい\(\,x\,\)を引けば）
必ず正（＋）として増加量が出てきますが、
\(\,y\,\)は増加するときもあれば、
減少するときもあります。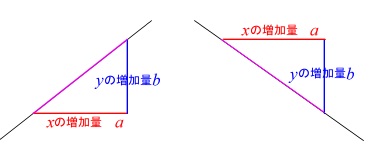だから
　変化の割合は正の場合と負の場合がある
ので注意しておきましょう。

1次関数では変化の割合と傾きが同じ

変化の割合は
　\(\displaystyle \,\color{red}{変化の割合=\frac{　(\,y\,の増加量)　}{　(\,x\,増加量)　}}\,\)
となりますが、
\(\,1\,\)次関数は直線なので傾きがこの変化の割合に一致します。

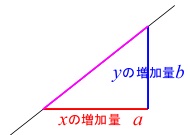
\(\,1\,\)次関数で
　「変化の割合と傾きが一致する」
ということを知ると、
『変化の割合』という言葉を忘れてしまう人が多いです。

『傾き』も大切ですが
『変化の割合』はすべての関数で使う
ので忘れないようにしておきましょう。
\(\,3\,\)年の\(\,y=ax^2\,\)の関数を学習するときでも
入試まででもついてくる言葉ですよ。

1次関数の求め方

高校に進学してからも関数をいろいろとあつかうことになりますが、
関数の決定、つまり関数を具体的に方程式にするというのはすべての関数の基本になります。

ただし、中学の間は4つしかありません。

　比例：\(\,y=ax\,\)
　反比例：\(\displaystyle \,y=\frac{a}{x}\,\)
　\(\,1\,\)次関数：\(\,y=ax+b\,\)
　\(\,x^2\,\)に比例する関数：\(\,y=ax^2\,\)

比例定数と傾きと切片を求めれば良いだけです。

ここでは\(\,1\,\)次関数を求める練習をしておきましょう。

問題２
　次の問に答えなさい。
(1) 変化の割合が\(\,-2\,\)で、\(\,x=3\,\)のとき\(\,y=0\,\)である\(\,1\,\)次関数の式を求めなさい。
(2) \(\,2\,\)点 \(\,(\,12\,,\,1\,)\,\) , \(\,(\,3\,,\,-2\,)\,\) を通る直線の式を求めなさい。

(1)
\(\,1\,\)次関数は、\(\,y=\color{red}{a}x+\color{blue}{b}\,\)と表せます。
つまり、\(\,\color{red}{a}\,\)と\(\,\color{blue}{b}\,\)を決めれば、\(\,1\,\)次関数が求まるということです。

問題に「変化の割合」という言葉が出てきていますが、
これは直線では「傾き」と同じものです。
　\(\displaystyle \,\color{red}{(変化の割合)=\frac{　y\,の増加量　}{　x\,の増加量　}}\,\)
で求まりますが、
直線では変化の割合いは常に一定だからです。

問題に「変化の割合が\(\,-2\,\)」と書いてあるので、
　傾き　\(\,\color{red}{a=-2}\,\)　と分かりますので、
　\(\hspace{4pt}\,y=\color{red}{-2}x+\color{blue}{b}\,\)
とかけます。
後は\(\,\color{blue}{b}\,\)を求めればいいだけです。

さらに問題には、
　「\(\,x=3\,\)のとき\(\,y=0\,\)である」
と書いてあります。
こういった条件は必ず問題に与えられていますので
見逃さないようにしましょう。

問題に必要無い条件はありません。

　\(\,y=\color{red}{-2}\,x+\color{blue}{b}\,\)
に
　\(x=3\,,\,y=0\)
を代入します。

　\(\begin{eqnarray}
(0)&=&-2\times (3)+\color{blue}{b}\\
&=&-6+\color{blue}{b}\\
6&=&\color{blue}{b}
\end{eqnarray}\)
だから求める１次関数は、
　\(\,\underline{　y=-2x+6　}\,\)
となります。答えです。

この問題は傾きが与えられましたが、
切片が先に与えられる問題もあります。
解き方は同じで、
通る\(\,1\,\)点があれば1つの係数が決められます。

　\(\,\color{red}{a}\,\)が先に決まるか、
　\(\,\color{blue}{b}\,\)が先に決まるか
の違いだけです。

\(\,1\,\)次関数には2つの係数しかありません。

1次関数と直線の方程式との違い

(2)問題の続きです。
『 \(\,2\,\)点 \(\,(\,12\,,\,1\,)\,,\,(\,3\,,\,-2\,)\,\) を通る直線の式を求めなさい。』

求める直線を\(\,y=ax+b\,\)とおいて、
　\(\,(12,1)\,,\,(3,-2)\,\)
の\(\,2\,\)点を代入し、
連立方程式を解いて\(\,a,b\,\)同時に求めることはできます。
それも一応覚えておいて下さい。

しかし、
ここでは「傾き」か「切片」のどちらか
を先に求める方法を考えます。

\(\,1\,\)次関数で\(\,2\,\)点を通る場合は、
「傾き」を先に求めます。
　「傾き」＝「変化の割合」
なので、
　\(\,x\,\)の増加量
と、
　\(\,y\,\)の増加量
をそれぞれ求めて、
割り算するだけなので簡単です。

このときに２つの座標を縦に並べると計算しやすいです。

　\(\,(\,\color{red}{12}\,,\hspace{8pt}\color{red}{1}\,)\,\)
　\(\,(\hspace{6pt}\color{blue}{3}\,,\,\color{blue}{-2}\,)\,\)

\(\,x\,\)の増加量は下の\(\,x\,\)座標から上の\(\,x\,\)座標を引いて
　\(\,(\color{blue}{3})-(\color{red}{12})=\color{red}{-9}\,\)
\(\,y\,\)の増加量は下の\(\,y\,\)座標から上の\(\,y\,\)座標を引いて
　\(\,(\color{blue}{-2})-(\color{red}{1})=\color{blue}{-3}\,\)
これから変化の割合、直線の傾き\(\,\color{red}{a}\,\)は
　\(\displaystyle \color{red}{a}=\frac{\color{blue}{-3}}{\color{red}{-9}}=\frac{1}{3}\)
と求まります。

変化の割合を求めるときは上で計算したように
同じ方向に引き算することが大切です。

一方だけを逆にすると、
傾きの正負が違ってきます。
下から上の座標を引くと決めておくといいですよ。
　　
何故、上から下を引かないのか？
上から下を引けば正の数で見やすいのでは？

と感じるでしょう。

確かにこの場合は上から下を引いた方が見やすいですが、
変化の割合を求めるのは\(\,2\,\)点間です。

関数の問題に与えられる座標は\(\,x\,\)座標の小さい方から与えられることが多いので、
縦に並べるとき、下に来る\(\,x\,\)座標の方が大きいことが多くなります。

変化の割合を求めるとき、分母にくるのは\(\,xの\,\)増加量なので、
分母が負の数になるより、正の値にすることを多くしたいので、
　『下から上を引く』
と統一しておくと考えることが少なくなるという理由です。

⇒　全国の公立高校入試数学過去問の解答解説

あちこちの都道府県で変化の割合問題は出てきます。
座標の与えられ方がどうなっているか確認しておくと良いです。

どちらでも良いですよ。
引く方向を\(\,x\,\)と\(\,y\,\)で同じにしておけば問題ありません。

傾きが分かったので求める直線は、
　\(\hspace{4pt}\displaystyle y=\frac{1}{3}x+\color{blue}{b}\)
というところまでは分かりました。

後は、切片の\(\,\color{blue}{b}\,\)ですが、
２つの点のどっちでもいいので代入すると求まります。

\(\,(\,12\,,\,1\,)\,\)を代入しましょうか。

　\(\begin{eqnarray}\displaystyle
(1)&=&\frac{1}{3}\times (12)+\color{blue}{b}\\
1&=&4+\color{blue}{b}\\
1-4&=&\color{blue}{b}\\
-3&=&\color{blue}{b}\\
\color{blue}{b}&=&-3
\end{eqnarray}\)

もちろん\(\,(3,-2)\,\)を代入しても同じ\(\,\color{blue}{b}\,\)が出てきます。

　\(\begin{eqnarray}\displaystyle
(-2)&=&\frac{1}{3}\times (3)+\color{blue}{b}\\
-2&=&1+\color{blue}{b}\\
-2-1&=&\color{blue}{b}\\
-3&=&\color{blue}{b}\\
\color{blue}{b}&=&-3
\end{eqnarray}\)

同じでなければ計算ミスしていますよ。
時間はかからないので見直しとして両方で確認しておくと良いです。
　
代入するときは正の数でも負の数でもできるだけ（かっこ）を付けておきましょう。
暗算を減らし、計算ミスを減らすためです。

⇒　代入とは？文字式に代入するときのポイントと項と同類項(中学1年)

計算ミスの多くは代入する時点でよく起こります。

よって求める直線の式は、
　\(\hspace{4pt}\displaystyle \underline{　y=\frac{1}{3}x-3　}\)

ところで、
(1)と(2)の問題の聞き方が違うことに気が付いていますか？

(1)は「\(\,1\,\)次関数を求めよ」なのに、
(2)は「直線の式を求めよ」となっています。

でも答えは同じ形ですよね。
言葉は違いますが同じことを求めているのです。

　「直線の方程式」＝「\(\,1\,\)次関数」

といってもいいくらいなんです。

違う場合は２つだけあります。

それは、

　\(\,x\,\)軸に平行な直線
と、
　\(\,y\,\)軸に平行な直線
です。

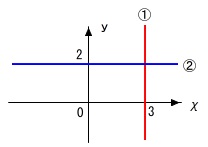
例えば、図のような直線は、
　①が\(\,y\,\)軸に平行で\(\,\color{red}{x=3}\,\)と表され、
　②が\(\,x\,\)軸に平行で\(\,\color{blue}{y=2}\,\)と表されますが、
\(\,1\,\)次関数ではありません。