2018年(平成30年)度大阪府公立高校入試C問題2平面図形の解説

2018年(平成30年)度に大阪府で行われた公立高校入試C問題第2問の平面図形問題の解説です。
第2問では角度を文字で表す、相似の証明、線分の長さ、部分面積を求めますが、
条件を使い切れば計算もそれほどややこしいものはありませんので最後まで誘導にのって終わります。

問題は大阪府でも解答とともに公開していくれています。

⇒　2018年大阪府公立入試C問題

　\(\,\large{2}\,\)

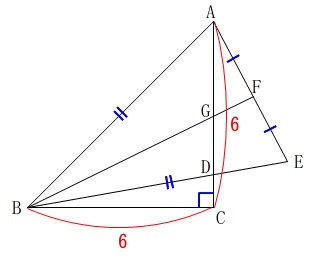
問題に与えられている条件を書き出します。

点を表す記号は図の中に示されている点の位置にあります。

　\(\,\mathrm{△ABC}\,\)は\(\,\mathrm{∠ACB=90°}\,\)の直角二等辺三角形
　\(\,\mathrm{AC=BC}\,\)
　\(\,\mathrm{BE=BA}\,\)
　\(\,\mathrm{F}\,\)は線分\(\,\mathrm{AE}\,\)の中点
これらの条件から加えられる条件がありますので足しておきます。

\(\,\mathrm{△ABC}\,\)が直角二等辺三角形なので
　\(\,\mathrm{∠CAB=∠CBA=45°}\,\)

　\(\,\mathrm{BE=BA}\,\)
と
　\(\,\mathrm{F}\,\)は線分\(\,\mathrm{AE}\,\)の中点
なので
　\(\,\mathrm{BF}\,\)は二等辺三角形\(\,\mathrm{BAE}\,\)の頂角の二等分線

分かることは図に書き込んでおきましょう。
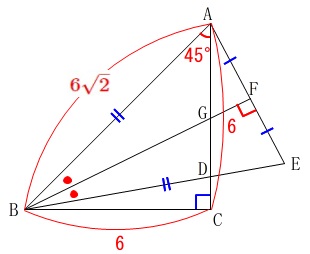他にもいえることはあります。
　\(\mathrm{BE}=\color{red}{6\sqrt{2}}\)
などは図がゴチャゴチャしそうなので書いていませんが、
この図の条件は最後まで使える条件ですよ。

ここまでの条件が書き出せていれば後は一気に進みます。
問題を解いていきます。

(1)
\(\,\mathrm{∠ABE}=a^{\circ}\,\)とすると
　\(\displaystyle \,\mathrm{∠ABF}=\color{red}{\frac{1}{2}a^{\circ}}\,\)
求めたいのは\(\,\mathrm{∠AGB}\,\)ですが先に\(\,\mathrm{∠\color{magenta}{BGD}}\,\)を求めます。

答えは「度」で表すので数値だけで計算します。

　\(\displaystyle ∠\color{magenta}{\mathrm{BGD}}=45+\frac{1}{2}\,a\,\)

よって

　\(\begin{eqnarray}\displaystyle
∠\mathrm{AGB}&=&180-\left(\,45+\frac{1}{2}a\,\right)\\
&=&\underline{　135-\frac{1}{2}\,a　}　（度）
\end{eqnarray}\)

(2)
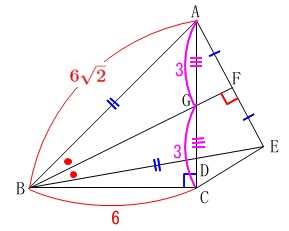
条件が加わります。

　\(\,\mathrm{AG=GC}\,\)
①
中点連結定理から
　\(\,\mathrm{GF}\, /\!/ \,\mathrm{CE}\,\)
　\(\,\mathrm{CE=2GF}\,\)
また
　\(\,\mathrm{GF}\, /\!/ \,\mathrm{CE}\,\)
なので
　\(\,\mathrm{BF}\, /\!/ \,\mathrm{CE}\,\)

平行線の錯角は等しいので、

　\(\,\mathrm{∠\color{red}{GBD}=∠\color{red}{CED}}\,　･･･ア\)
　\(\,\mathrm{∠\color{blue}{DGB}}=\mathrm{∠\color{blue}{DCE}}\,　･･･イ\)

対頂角は等しいから

　\(\,\mathrm{∠BDG=∠EDC}\,　･･･ウ\)

もいえます。
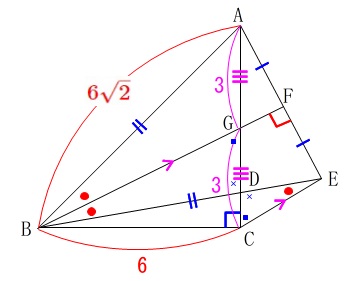ア、イ、ウのどれか2つで良いので取り上げてそれぞれ等しいことをいえば、

　\(\,2\,\)組の角がそれぞれ等しい

相似条件がいえるので

　\(\,\mathrm{△BDG}\,\)　∽　\(\,\mathrm{△EDC}\,\)

長々と説明していますが、図の中では短時間で終わっています。

②
線分\(\,\mathrm{GF}\,\)の長さを求めます。
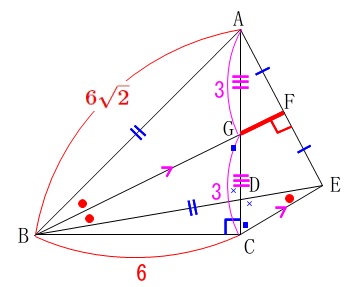①で中点連結定理や相似に気がつくので\(\,\mathrm{CE}\,\)を求めたいところですが、
長さの条件が足りていません。

分かる長さと他の相似を探してみるとすぐに見つかりますが、
使える条件がいくつかあるので迷うところです。

どれを使いましょう？笑

こういうときはきがついた条件で突っ走った方がはやいです。

長さについては、直角三角形\(\,\mathrm{BCG}\,\)に三平方の定理を利用して、
　\(\begin{eqnarray}\displaystyle
\mathrm{BG^2}&=&\mathrm{BC^2+CG^2}\\
&=&6^2+3^2\\
&=&45\\
\mathrm{BG}&=&3\sqrt{5}　(\mathrm{BG}\,＞\,0)
\end{eqnarray}\)

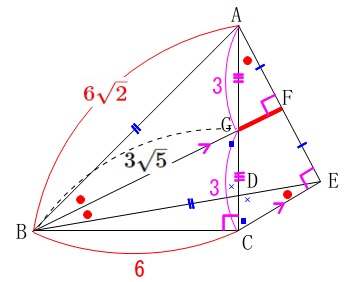相似については①で証明した相似もありますが、
　\(\,\mathrm{△BGC}\,\)　∽　\(\,\mathrm{△ACE}\,\)
や
　\(\,\mathrm{△BGC}\,\)　∽　\(\,\mathrm{△AGF}\,\)
などもあります。

となると\(\,\mathrm{CE}\,\)を求めるよりダイレクトに\(\,\mathrm{GF}\,\)が求まる方が良いですよね。
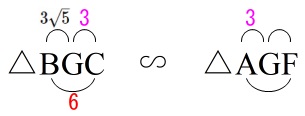比例式を立てれば良いだけです。

　\(\begin{eqnarray}\displaystyle
\mathrm{BG:AG}&=&\mathrm{GC:GF}\\
\mathrm{BG}\times \mathrm{GF}&=&\mathrm{AG}\times \mathrm{GC}\\
3\sqrt{5}\times \mathrm{GF}&=&3\times 3\\
\mathrm{GF}&=&\frac{3\times 3}{3\sqrt{5}}\\
&=&\underline{　\frac{3\sqrt{5}}{5}　}
\end{eqnarray}\)

ここで
　\(\displaystyle \,\mathrm{CE=2\times \frac{3\sqrt{5}}{5}}=\frac{6\sqrt{5}}{5}\,\)
までは求めて、図に書き込んでおきます。

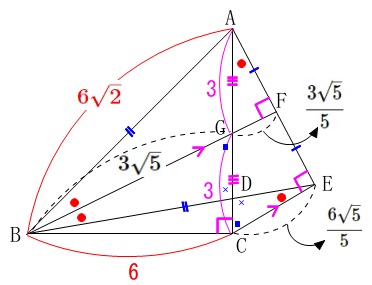
③
\(\,\mathrm{△ABD}\,\)の面積を求めます。

　底辺を\(\,\mathrm{AD}\,\)
　高さを\(\,\mathrm{BC}\,\)

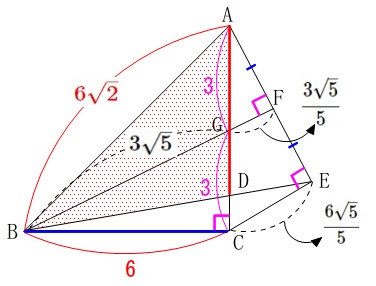
の三角形の面積を求めることになるので\(\,\mathrm{AD}\,\)の長さが必要になります。

これは①で証明した相似を利用すれば\(\,\mathrm{GD}\,\)がすぐに求まるでしょう。

　\(\mathrm{AD=AG+GD}\)
で\(\,\mathrm{AG=3}\,\)だから底辺が出てきます。

または
　\(\,\mathrm{△ABD=△ABC-△BDC}\,\)
なので①の相似を利用して\(\,\mathrm{DC}\,\)を求めて
　\(\displaystyle \,\mathrm{△BDC=\frac{1}{2}\times BC\times DC}\,\)
を\(\,\mathrm{△ABC}\,\)から引いても良いです。

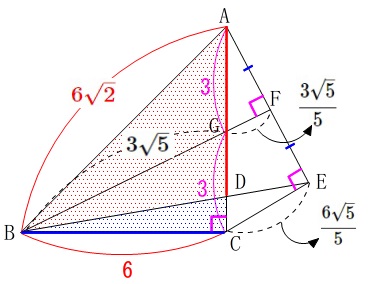
どちらにしても①の相似から\(\,\mathrm{GD}\,\)か\(\,\mathrm{DC}\,\)は求めておく必要がありそうです。
というか迷う間に出せるので、とりあえず、として求めておいても大した時間はかかりません。
長さは出ませんが相似比は出ます。

　\(\begin{eqnarray}\displaystyle
\mathrm{DG:DC}&=&\mathrm{BG:EC}\\
&=&3\sqrt{5}:\frac{6\sqrt{5}}{5}\\
&=&15:6\\
&=&5:2
\end{eqnarray}\)
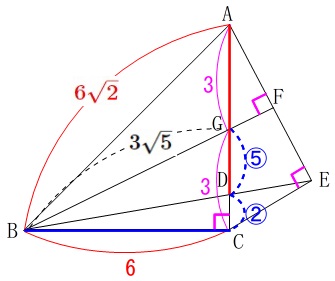両方求めておきますので面積は好きな方で出して下さい。

　\(\begin{eqnarray}\displaystyle
\mathrm{GD}&=&\frac{5}{5+2}\times \mathrm{GC}\\
&=&\frac{5}{7}\times 3\\
&=&\color{blue}{\frac{15}{7}}
\end{eqnarray}\)

　\(\begin{eqnarray}\displaystyle
\mathrm{DC}&=&\frac{2}{5+2}\times \mathrm{GC}\\
&=&\frac{2}{7}\times 3\\
&=&\color{blue}{\frac{6}{7}}
\end{eqnarray}\)

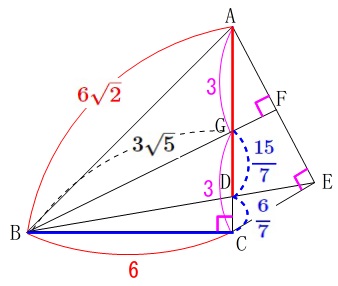求める\(\,\mathrm{△ABD}\,\)の面積は

　\(\begin{eqnarray}\displaystyle
\mathrm{△ABD}&=&\frac{1}{2}\times \mathrm{AD}\times \mathrm{BC}\\
&=&\frac{1}{2}\times (\mathrm{\color{magenta}{AG}+\color{blue}{GD}})\times \mathrm{BC}\\
&=&\frac{1}{2}\times \left(\color{magenta}{3}+\color{blue}{\frac{15}{7}}\right)\times 6\\
&=&\frac{1}{2}\times \frac{21+15}{7}\times 6\\
&=&\frac{1}{2}\times \frac{36}{7}\times 6\\
&=&\underline{　\frac{108}{7}　}
\end{eqnarray}\)

または

　\(\begin{eqnarray}\displaystyle
\mathrm{△ABD}&=&\mathrm{△ABC-△BDC}\\
&=&\frac{1}{2}\times 6\times 6-\frac{1}{2}\times \frac{6}{7}\times 6\\
&=&18-\frac{18}{7}\\
&=&\frac{126-18}{7}\\
&=&\underline{　\frac{108}{7}　}
\end{eqnarray}\)

他にも\(\,\mathrm{△BCG}\,\)　∽　\(\,\mathrm{△AEC}\,\)で
　\(\,\mathrm{BC:CG=6:3=2:1}\,\)
なので
　\(\displaystyle \,\mathrm{CE=EF=FA=\frac{6\sqrt{5}}{5}}\,\)

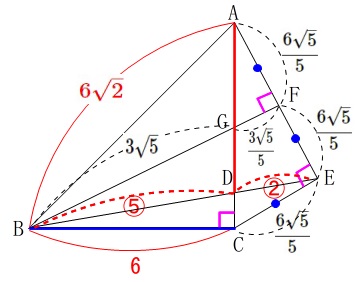
また
　\(\begin{eqnarray}\displaystyle
\mathrm{BF}&=&\mathrm{BG+GF}\\
&=&3\sqrt{5}+\frac{3\sqrt{5}}{5}\\
&=&\frac{15\sqrt{5}+3\sqrt{5}}{5}\\
&=&\frac{18\sqrt{5}}{5}
\end{eqnarray}\)
なので
　\(\begin{eqnarray}\displaystyle
△\mathrm{ABE}&=&\frac{1}{2}\times \mathrm{AE}\times \mathrm{BF}\\
&=&\frac{1}{2}\times \frac{12\sqrt{5}}{5}\times \frac{18\sqrt{5}}{5}\\
&=&\frac{108}{5}
\end{eqnarray}\)

①の相似から\(\,\mathrm{BD:DE=5:2}\,\)なので
　\(\begin{eqnarray}\displaystyle
△\mathrm{ABD}&=&\frac{5}{5+2}\times △\mathrm{ABE}\\
&=&\frac{5}{7}\times \frac{108}{5}\\
&=&\underline{　\frac{108}{7}　}
\end{eqnarray}\)

と求めることもできますが、ちょっと遠回りに思えるでしょうか。

\(\,\large{2}\,\)は以上です。

図を2つ与えてくれているので思うほど時間はかからないのですが、
条件を使い切ることがポイントですね。

⇒　3　（近日公開？非公開？）

\(\,\large{3}\,\)は立体の中の面積、線分、体積ですが、
一つひとつていねいに抜き出せば教科書通りで十分です。

⇒　2018年(平成30年)度大阪府公立高校入試C問題の解説

\(\,\large{1}\,\)は小問集合です。