2018年(平成30年)度大阪府公立高校入試C問題3空間図形の解説

2018年(平成30年)度に大阪府で行われた公立高校入試C問題第3問の空間図形（立体）問題の解説です。
第3問では立体内の三角形の面積、線分、および立体の1部分の体積を求めます。
線分の長さを求める問題がいくつかあります。
立体も形を変えるので全体通じての条件と、問題ごとの条件をしっかり見極めることがポイントです。

問題は大阪府でも解答とともに公開していくれています。

⇒　2018年大阪府公立入試C問題

　\(\,\large{3}\,\)

(1)と(2)では柱体の形が違うので注意が必要です。

(1)はおなじみの三角柱で正三角形と長方形が垂直になっています。

(2)は斜めに向いた正三角形ですが、立体の中に垂直な条件がありますので立体問題としての方針は同じで良いですよ。

全体に通じる条件を抜き出しておきましょう。

　四角形\(\,\mathrm{BCFE}\,\)は長方形
　\(\,\mathrm{△ABC\,,\,△DEF}\,\)は正三角形で平行
　 \(\,\mathrm{BC=6}\,\)
　 \(\,\mathrm{CF=8}\,\)
　 \(\,\mathrm{AG=2}\,\)
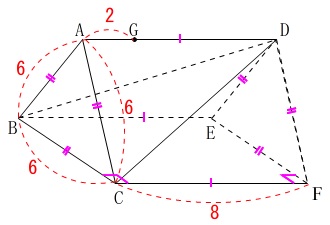問題の中で他に書いてあることは必然的についてくる性質なので書いていません。

(1)四角形\(\,\mathrm{ACFD}\,\)が長方形なので、
正三角形と\(\,\mathrm{BCFE}\,\)も垂直で、普通の三角柱として考えれば良いです。

条件が追加されます。

　\(\,\mathrm{GH　⊥　DC}\,\)
　\(\,\mathrm{GI　⊥　DB}\,\)

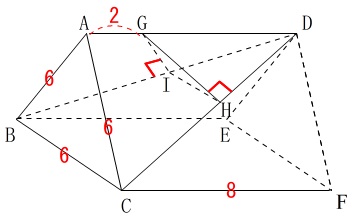
①
\(\,\mathrm{△ABC}\,\)は\(\,1\,\)辺が\(\,6\,\)の正三角形なので

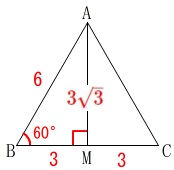
　\(\begin{eqnarray}
△\mathrm{ABC}&=&\frac{1}{2}\times \mathrm{BC}\times \mathrm{AM}\\
&=&\frac{1}{2}\times 6\times 3\sqrt{3}\\
&=&\underline{　9\sqrt{3}　}
\end{eqnarray}\)

②
線分\(\,\mathrm{GH}\,\)の長さです。

線分\(\,\mathrm{GH}\,\)を含む面を抜き出します。
\(\,\mathrm{△GHI}\,\)ということも考えられますが、先ずは素直に\(\,\mathrm{△ADC}\,\)または長方形\(\,\mathrm{ACFD}\,\)を抜き出しましょう。
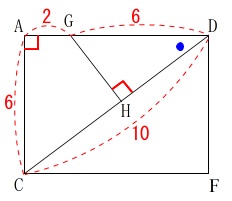相似を使って\(\,\mathrm{GH}\,\)を求めますが\(\,\mathrm{DC}\,\)が必要になるので、
直角三角形\(\,\mathrm{ADC}\,\)に三平方の定理を用いて
　\(\begin{eqnarray}
\mathrm{DC^2}&=&\mathrm{AC^2+AD^2}\\
&=&6^2+8^2\\
&=&100\\
\mathrm{DC}&=&10　(\mathrm{DC}\,＞\,0)
\end{eqnarray}\)
を先に出しておきました。

\(\,2\,\)組の角がそれぞれ等しいので
　\(\,\mathrm{△DAC}\,\)　∽　\(\,\mathrm{△DHG}\,\)
なので

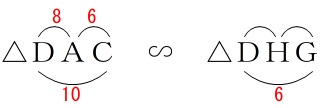
　\(\begin{eqnarray}
\mathrm{DC:DG}&=&\mathrm{CA:GH}\\
\mathrm{DC\times GH}&=&\mathrm{DG\times CA}\\
10\times \mathrm{GH}&=&6\times6\\
\mathrm{GH}&=&\frac{6\times 6}{10}\\
&=&\underline{　\frac{18}{5}　}
\end{eqnarray}\)

③
今度は\(\,\mathrm{HI}\,\)の長さです。
△\(\,\mathrm{GHI}\,\)を抜き出すか、△\(\,\mathrm{DBC}\,\)を抜き出すかです。

\(\,\mathrm{△GHI}\,\)は\(\,\mathrm{GH=GI}\,\)の二等辺三角形だから使えそうに思えますが、頂角が分かっていないのですんなりとはいきそうもありません。

②の相似から\(\,\mathrm{DH}\,\)も求まるので\(\,\mathrm{△DBC}\,\)を使って見ます。
その前に\(\,\mathrm{DC}\,\)を分割した比を求めておきます。
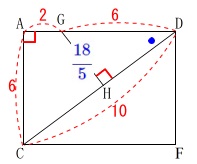必要無いけど②の\(\,\mathrm{GH}\,\)を書き込みました。
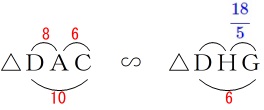使うのはこちらです。

　\(\begin{eqnarray}
\mathrm{DA:DH}&=&\mathrm{DC:DG}\\
8:\mathrm{DH}&=&10:6\\
10\times \mathrm{DH}&=&6\times 8\\
\mathrm{DH}&=&\frac{6\times 8}{10}\\
&=&\color{blue}{\frac{24}{5}}
\end{eqnarray}\)

比でも良いのですが、分かり易くするために\(\,\mathrm{CH}\,\)も具体的に求めておきます。

　\(\begin{eqnarray}
\mathrm{CH}&=&\mathrm{DC-DH}\\
&=&10-\frac{24}{5}\\
&=&\frac{50-24}{5}\\
&=&\color{blue}{\frac{26}{5}}
\end{eqnarray}\)

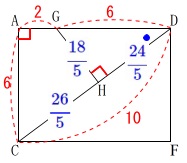簡単な比にしておきましょう。

　\(\begin{eqnarray}\displaystyle
\mathrm{DH:CH}&=&\frac{24}{5}:\frac{26}{5}\\
&=&\color{magenta}{12:13}
\end{eqnarray}\)

\(\,\mathrm{△GHD}\,\)と\(\,\mathrm{△GID}\,\)は合同なので\(\,\mathrm{IH \,/\!/\, BC}\,\)です。
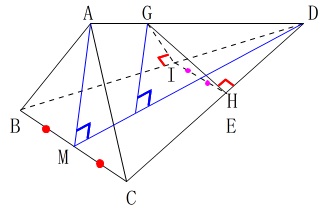問題全部を通じて\(\,\mathrm{AD}\,\)上の点から\(\,\mathrm{△BCD}\,\)に垂線を下ろすと\(\,\mathrm{DM}\,\)上に下ります。
（(1)では\(\,\mathrm{AM　⊥　DM}\,\)でもあります。）
ということは、\(\,\mathrm{GH=GI}\,\)もいえるということです。

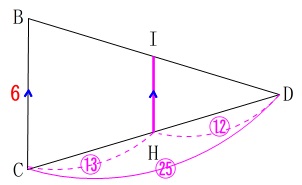
　\(\,\mathrm{△DBC}\,\)　∽　\(\,\mathrm{△DIH}\,\)
で\(\,\mathrm{BC=6}\,\)と\(\,\mathrm{DC:DH=25:12}\,\)が分かっているので

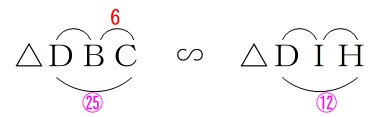
　\(\begin{eqnarray}\displaystyle
\mathrm{DC:DH}&=&\mathrm{BC:\color{red}{IH}}\\
25:12&=&6:\mathrm{\color{red}{IH}}\\
25\times \mathrm{\color{red}{IH}}&=&6\times 12\\
\mathrm{\color{red}{HI}}&=&\frac{6\times 12}{25}\\
&=&\underline{　\frac{72}{25}　}
\end{eqnarray}\)

説明はややこしいですがやっていることは単純な比例計算です。

(2)
条件が少し変わって正三角形\(\,\mathrm{ABC}\,\)が斜めを向きます。
ただ、(1)に入る前の条件は変わっていません。

条件は
　\(\,\mathrm{GC=5}\,\)
だけですが、
　\(\mathrm{BJ}　⊥　\mathrm{AD}\)
もいってくれています。

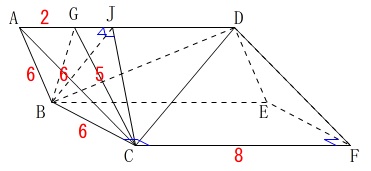
また全体の条件から
　\(\,\mathrm{AD}\,\)から長方形\(\,\mathrm{BCFE}\,\)に下ろした垂線は、
　\(\,\mathrm{BC}\,\)、\(\,\mathrm{FE}\,\)の中点を結んだ直線上
に下ります。
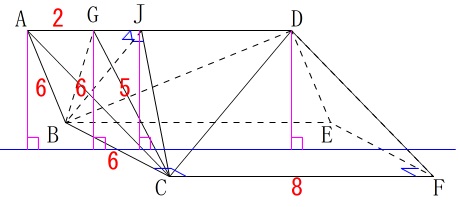なので(1)で言えた合同は同じなので
　\(\mathrm{JC}　⊥　\mathrm{AD}\)
これは問題の図に示してくれています。

後は簡単なのでさっさと済ませてしまいましょう。

①
線分\(\,\mathrm{GJ}\,\)の長さを求めますので、\(\,\mathrm{△ACJ}\,\)を抜き出します。
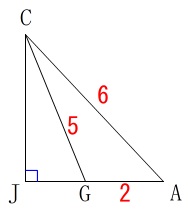公式化するのもめんどうなので、文字でおいて求めます。

　\(\,\mathrm{GJ}=x\,\)とすると

\(\,\mathrm{△CJG}\,\)から

　\(\begin{eqnarray}
\mathrm{CG^2}&=&\mathrm{CJ^2+JG^2}\\
5^2&=&\mathrm{CJ^2}+x^2\\
\mathrm{\color{red}{CJ^2}}&=&25-x^2
\end{eqnarray}\)

\(\,\mathrm{△CJA}\,\)から

　\(\begin{eqnarray}
\mathrm{CA^2}&=&\mathrm{CJ^2+AJ^2}\\
6^2&=&\mathrm{CJ^2}+(x+2)^2\\
\mathrm{\color{red}{CJ^2}}&=&36-(x+2)^2
\end{eqnarray}\)

これらの右辺どうしが等しくなるので、

　\(\begin{eqnarray}\displaystyle
25-x^2&=&36-(x+2)^2\\
25-x^2&=&36-(x^2+4x+4)\\
25\color{blue}{-x^2}&=&36\color{blue}{-x^2}-4x-4\\
25&=&32-4x\\
4x&=&36-4-25\\
&=&7\\
x&=&\underline{　\frac{7}{4}　}
\end{eqnarray}\)

②
立体\(\,\mathrm{GBCD}\,\)の体積を求めます。

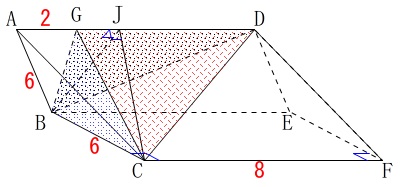
　底面は\(\,\mathrm{△JBC}\,\)
　高さは\(\,\mathrm{GD}\,\)の錐体

なのでそれぞれを計算すれば終わりです。
長さを書き込むともう少し分かり易くなるでしょうか。

　\(\displaystyle \mathrm{GJ}=\frac{7}{4}\)
なので
　\(\begin{eqnarray}\displaystyle
\mathrm{JD}&=&\mathrm{AD-AJ}\\
&=&\mathrm{AD}-(\mathrm{AG}+\mathrm{GJ})\\
&=&8-\left(2+\frac{7}{4}\right)\\
&=&6-\frac{7}{4}\\
&=&\frac{24-7}{4}\\
&=&\frac{17}{4}
\end{eqnarray}\)
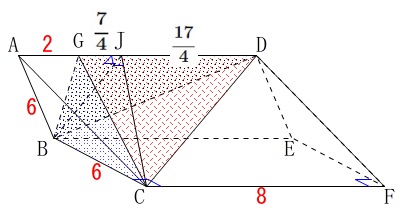しかし、この高さは底面積が同じなので\(\,\mathrm{GD=6}\,\)で計算しても同じです。

底面となる\(\,\mathrm{△JBC}\,\)を抜き出します。
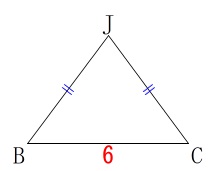この三角形面積を出すのに高さが必要ですが、\(\,\mathrm{JC}\,\)の長さを出していませんでした。

①で用いた三平方の定理から
　\(\begin{eqnarray}\displaystyle
\mathrm{\color{red}{CJ^2}}&=&25-x^2\\
&=&25-\left(\frac{7}{4}\right)^2\\
&=&25-\frac{49}{16}\\
&=&\frac{25\times 16-49}{16}\\
&=&\frac{400-49}{16}\\
&=&\color{red}{\frac{351}{16}}\\
\end{eqnarray}\)
※
平方根まで処理していませんが、次の三平方の定理と組み合わせるので平方のまま残してあります。

\(\,\mathrm{J}\,\)から\(\,\mathrm{BC}\,\)に垂線を引いて\(\,\mathrm{BC}\,\)との交点を\(\,\mathrm{T}\,\)とすると、
\(\,\mathrm{JT}\,\)が\(\,\mathrm{△JBC}\,\)の高さになります。
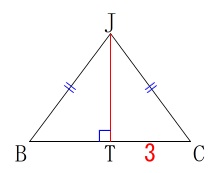このとき三平方の定理から
　\(\begin{eqnarray}\displaystyle
\mathrm{JT^2+TC^2}&=&\mathrm{\color{red}{JC^2}}\\
\mathrm{JT^2}+3^2&=&\color{red}{\frac{351}{16}}\\
\mathrm{JT^2}&=&\frac{351}{16}-9\\
&=&\frac{351-9\times 16}{16}\\
&=&\frac{351-144}{16}\\
&=&\frac{207}{16}\\
\mathrm{JT}&=&\frac{3\sqrt{23}}{4}　(\mathrm{\,JT\,＞\,0\,})
\end{eqnarray}\)

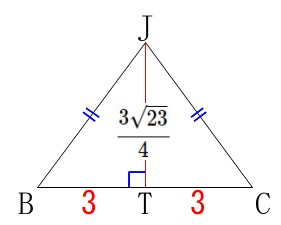底面\(\,\mathrm{△JBC}\,\)の面積は

　\(\begin{eqnarray}\displaystyle
\mathrm{△JBC}&=&\frac{1}{2}\times \mathrm{BC}\times \mathrm{JT}\\
&=&\frac{1}{2}\times 6\times \frac{3\sqrt{23}}{4}\\
&=&\frac{9\sqrt{23}}{4}
\end{eqnarray}\)

よって求める立体（三角錐）の体積\(\,\mathrm{V}\,\)は、

　\(\begin{eqnarray}\displaystyle
\mathrm{V}&=&\frac{1}{3}\times \mathrm{△JBC} \times (\mathrm{GJ+JD})\\
&=&\frac{1}{3}\times \mathrm{△JBC}\times \mathrm{GD}\\
&=&\frac{1}{3}\times \frac{9\sqrt{23}}{4}\times 6\\
&=&\underline{　\frac{9\sqrt{23}}{2}　}
\end{eqnarray}\)

立体の体積は、
　底面が\(\,\mathrm{△JBC}\,\)
　高さが\(\,\mathrm{GJ}\,\)と\(\,\mathrm{JD}\,\)
の2つの立体の和です。
だから別々に計算して加えると
　\(\begin{eqnarray}\displaystyle
\mathrm{V}&=&\frac{1}{3}\times \mathrm{△JBC} \times \mathrm{GJ}+\frac{1}{3}\times \mathrm{△JBC}\times \mathrm{JD}\\
&=&\frac{1}{3}\times \frac{3\sqrt{23}}{4}\times \frac{7}{4}+\frac{1}{3}\times \frac{3\sqrt{23}}{4}\times \frac{17}{4}\\
&=&\frac{1}{3}\times \frac{3\sqrt{23}}{4} \times \left(\frac{7}{4}+\frac{17}{4}\right)\\
&=&\frac{1}{3}\times \frac{3\sqrt{23}}{4}\times 6\\
&=&\underline{　\frac{9\sqrt{23}}{2}　}
\end{eqnarray}\)

としても良いですが、底面が共通なので高さは1つと考えた方がはやいです。

2018年度の大阪C問題は以上です。

⇒　2018年(平成30年)度大阪府公立高校入試C問題の解説

\(\,\large{1}\,\)から見直して問題構成を頭に叩き込んで対策すると良いです。

⇒　大阪府公立高校入試数学の過去問と解答解説

2019年度の解説もしますので確認しておいてください。