2018年(平成30年)度大阪府公立高校入試C問題の数学解説

2018年(平成30年)度に大阪府で行われた公立高校入試C問題の数学の解説です。
問題1から3までありますがここでは1の小問集合の解説になります。
C問題は学校選択で発展的な内容で、ある程度数学の基本はできている中学生が受験することになるので解説も簡単に済ませておきます。

問題は大阪府でも解答とともに公開していくれています。

⇒　2018年大阪府公立入試C問題

　\(\,\large{1}\,\)　

『覚え太郎』会員向けに説明するので「何故そうするのか？」の部分が飛ぶかもしれませんがご容赦ください。

(1)
単なる式の計算です。

分数計算ですが分子の計算に集中します。

　\(\hspace{10pt}\displaystyle \frac{5a-2b}{4}-\frac{3a-7b}{5}\\
\displaystyle =\frac{5(5a-2b)-4(3a-7b)}{20}\\
\displaystyle =\frac{25a-10b-12a+28b}{20}\\
\displaystyle =\underline{　\frac{13a+18b}{20}　}\)

(2)
代入計算です。
与式を簡単にしてからですね。

　\(\hspace{10pt}\displaystyle \frac{1}{6}a^2b\times a^3b^2\div\left(-\frac{1}{2}ab\right)^2\\
\displaystyle =\frac{a^2b\times a^3b^2}{6}\times \frac{4}{a^2b^2}\\
\displaystyle =\frac{2}{3}a^3b
\)

\(\displaystyle a=-3\,,\,b=\frac{1}{4}\)　を代入します。

　\(\hspace{10pt}\displaystyle \frac{2}{3}a^3b\\
\displaystyle =\frac{2}{3}\times (-3)^3\times \left(\frac{1}{4}\right)\\
\displaystyle =\underline{　-\frac{9}{2}　}
\)

符号には気をつけて見直しはしっかりとしましょう。

(3)
無理数の展開計算です。

⇒　文字式の展開公式で覚えなくて良い公式と覚えた方が良い公式(中学3年)

文字式でも無理数でも同じように展開公式を利用して計算するだけです。

　\(\hspace{10pt}(3\sqrt{3}+\sqrt{2})(3\sqrt{3}-\sqrt{2})-(\sqrt{6}-4)^2\\
=(3\sqrt{3})^2-(\sqrt{2})^2-(6-8\sqrt{6}+4^2)\\
=27-2-(6-8\sqrt{6}+16)\\
=25-(22-8\sqrt{6})\\
=25-22+8\sqrt{6}\\
=\underline{　3+8\sqrt{6}　}
\)

(4)
連立方程式も方程式なので解は方程式に代入して成り立ちます。
当たり前のことですが、方程式を成り立たせるものが方程式の解ですよ。

⇒　方程式とは？方程式の解と移項とは？基本問題の解き方(中１数学)

連立方程式

　\( \begin{cases}
\hspace{7pt} ax+by=-11\\ \\
\hspace{7pt} bx+ay=17
\end{cases}\)

の解が
　\(\,x=1\,,\,y=-3\,\)
なので代入すると

　\( \begin{cases}
\hspace{7pt} a\times (1)+b\times (-3)=-11\\ \\
\hspace{7pt} b\times (1)+a\times (-3)=17
\end{cases}\)

\(\,a,b\,\)の連立方程式に変わりました。

　　\( \begin{cases}
\hspace{7pt} a-3b&=&-11\\ \\
\hspace{7pt} -3a+b&=&17
\end{cases}\)

これを解くと
　\(\,\underline{　a=-5\,,\,b=2　}\,\)
　
(5)
\(\,6\,\)行の文章になっている確率の問題ですが、

　箱\(\,\mathrm{\color{red}{A}}\,\)：　\(\color{black}{\fbox{1}}\)　\(\color{black}{\fbox{4}}\)　\(\color{black}{\fbox{5}}\)
から\(\,2\,\)枚取り出す。

　箱\(\,\mathrm{\color{blue}{B}}\,\)：　\(\color{black}{\fbox{3}}\)　\(\color{black}{\fbox{7}}\)　\(\color{black}{\fbox{9}}\)
から\(\,1\,\)枚取り出す。

このとき取り出した\(\,3\,\)枚のカードの数字を小さい順に\(\,a\,,\,b\,,\,c\,\)とするとき
　\(\,\color{magenta}{a+c=2b}\,\)
となる確率を求める問題です。

\(\,\mathrm{\color{red}{A}}\,\)から\(\,2\,\)枚取り出す取り出し方は\(\,3\,\)通りしかありません。

　\(\,(\,1\,,\,4\,)\,,\,(\,1\,,\,5\,)\,,\,(4\,,\,5\,)\,\)

この\(\,1\,\)組に対し、\(\,\mathrm{\color{blue}{B}}\,\)を\(\,1\,\)枚加える組み合わせはそれぞれ\(\,3\,\)通りしかありません。

全部でたかが\(\,9\,\)通りです、書き出しましょう。
表じゃなくていいです。
樹形図「もどき」でも良いです。

　\(\begin{array}{|c|c|c|} \hline
\mathrm{\color{red}{A}} & \mathrm{\color{red}{A}} & \mathrm{\color{blue}{B}} \\ \hline
1 & 4 & 3 \\ \hline
1 & 4 & 7 \\ \hline
1 & 4 & 9 \\ \hline
1 & 5 & 3 \\ \hline
1 & 5 & 7 \\ \hline
1 & 5 & 9 \\ \hline
4 & 5 & 3 \\ \hline
4 & 5 & 7 \\ \hline
4 & 5 & 9 \\ \hline
\end{array}\)

小さい順に並べ替え\(\,2b\,\)も加えると

　\(\begin{array}{|c|c|c|c|} \hline
\color{red}{a} & b & \color{red}{c} & \color{blue}{2b}\\ \hline
1 & 3 & 4 & 6\\ \hline
\color{magenta}{1} & 4 & \color{magenta}{7} & \color{magenta}{8}\\ \hline
1 & 4 & 9 & 8\\ \hline
\color{magenta}{1} & 3 & \color{magenta}{5} & \color{magenta}{6}\\ \hline
1 & 5 & 7 & 10\\ \hline
\color{magenta}{1} & 5 & \color{magenta}{9} & \color{magenta}{10}\\ \hline
\color{magenta}{3} & 4 & \color{magenta}{5} & \color{magenta}{8}\\ \hline
4 & 5 & 7 & 10\\ \hline
4 & 5 & 9 & 10\\ \hline
\end{array}\)
※
表にすると見にくくなりました。笑

　\(\,\color{magenta}{a+c=2b}\,\)を満たすのは\(\,4\,\)通り
よって求める確率は

　\(\displaystyle \underline{　\frac{4}{9}　}\)

(6)
ヒスとクラムと平均値、中央値の2つの代表値の関係を聞いている問題です。

⇒　代表値とは？度数分布表の平均値,中央値の求め方と最頻値の答え方

\(\,20\,\)人うちの\(\,1\,\)人のデータを訂正したことで、
平均値が\(\,0.1\,\)大きくなったということは、
　\(\,20\times 0.1=2\,(冊)\)
増えたということです。

また中央値が変化しなかったということは、
訂正後のヒストグラムの中央値が\(\,7.5\,\)であることから

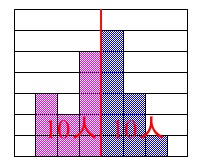
　\(\,5\,\)冊から\(\,7\,\)冊で\(\,10\,\)人
　\(\,8\,\)冊から\(\,10\,\)冊で\(\,10\,\)人

この人数は変わっていないということなので訂正した冊数は
　
　\(\,5\,\)冊から\(\,7\,\)冊
または
　\(\,8\,\)冊から\(\,10\,\)冊
しか考えられません。
※
中央値をまたいで変化はしていない、ということです。

ところが
　\(\,8\,\)冊から\(\,10\,\)冊
に訂正したとすると訂正前には\(\,10\,\)冊の\(\,1\,\)人がいなかったことになるので範囲は変わっています。
範囲も変化しなかったということなのでこれはあり得ません。

よって
　\(\color{black}{\fbox{　\(\,\underline{　5　}\,\)　}}\)冊から\(\color{black}{\fbox{　\(\,\underline{　7　}\,\)　}}\)冊に
訂正してヒストグラムを作ったことになります。　
　
(7)
文字式のあつかいです。

⇒　中学数学で使う文字式の一覧(奇数や偶数などの整数の表し方)

　\(\,a\,\)は\(\,2\,\)けたの奇数
　\(\,b\,\)は\(\,a\,\)の十の位の数と一の位の数を入れかえた自然数
とするとき
　　\(\displaystyle 20\,≦\,\frac{a+b}{8}\,≦\,21\)
を満たす\(\,aを\,\)すべて求める問題です。

けた数を入れかえる問題は文字式で何度も見ているでしょう。

十の位の数を\(\,\color{red}{x}\,\)、一の位の数を\(\,\color{blue}{y}\,\)とすると
\(\,x,y\,\)ともに\(\,1\,\)けたの自然数で
　
　\(a=10\color{red}{x}+\color{blue}{y}\)
　\(b=10\color{blue}{y}+\color{red}{x}\)

とおけて

　\(\displaystyle 20\,≦\,\frac{a+b}{8}\,≦\,21\)

を満たすとき

　\(\displaystyle 20\,≦\,\frac{11x+11y}{8}\,≦\,21\\ \\
160\,≦\,11(x+y)\,≦\,168\\ \\
14.5\cdots \,≦\,x+y\,≦15.2\cdots\,\)

よって
　\(\,x+y=15\,\)
これを満たす\(\,1\,\)けたの自然数\(\,(\,x\,,\,y\,)\)は

　\((\,6\,,\,9\,)\,,\,(\,7\,,\,8\,)\,,\,(\,8\,,\,7\,)\,,\,(\,9\,,\,6\,)\,\)

このうち\(\,a=10x+y\,\)が奇数なのは
　\(\,\underline{　69　}　と　\underline{　87　}\,\)

(8)
関数としてはもっと問題数を増やせますが、文字設定をして誘導なしで1つだけの質問です。
\(\,\mathrm{C}\,\)問題を選択する学校ではこれが当たり前だと思っていて良いですね。

ただ、文字設定をしてしまえば面積自体は単純なので難しくはありません。

条件を書き出します。

　\(\displaystyle \,m：y=\frac{1}{3}x^2\,\)

　\(\,\mathrm{A,B}\,\)は\(\,m\,\)上の点で\(\,x\,\)座標はそれぞれ\(\,-2\,\)と\(\,4\,\)
なので
　\(\displaystyle \,\mathrm{A\,\left(\,-2\,,\hspace{6pt}\frac{4}{3}\,\right)}\,\)
　\(\displaystyle \,\mathrm{B\,\left(\hspace{10pt}4\,,\,\frac{16}{3}\,\right)}\,\)

この\(\,2\,\)点から直線\(\,\mathrm{AB}\,\)と直線\(\,\mathrm{OB}\,\)の式を出しておきます。
直線\(\,\mathrm{OA}\,\)も出ますが必要ないのでここでは書きません。

\(\,2\,\)点\(\,\mathrm{A,B}\,\)から

　\(\,x\,の増加量=(4)-(-2)=6\,\)
　\(\displaystyle \,y\,の増加量=\frac{16}{3}-\frac{4}{3}=4\,\)

よって直線\(\,\mathrm{AB}\,\)の傾きは
　\(\displaystyle \frac{4}{6}=\frac{2}{3}\)

直線\(\,\mathrm{AB}\,\)の方程式は
　\(\displaystyle y=\frac{2}{3}x+b\)

とおけて、\(\,\mathrm{A,B}\,\)を通ることからどちらかを代入して

　\(\displaystyle y=\frac{2}{3}x+\frac{8}{3}\)

直線\(\,\mathrm{OB}\,\)は原点と点\(\,\mathrm{B}\,\)を通るので

　\(\displaystyle y=\frac{4}{3}x\)　

\(\,\mathrm{AC}\,\)は\(\,y\,\)軸と平行で\(\,\mathrm{C}\,\)は\(\,x\,\)軸上の点なので

　\(\mathrm{C}\,(\,-2\,,\,0\,)\)
　
ここまでを図示しておきます。
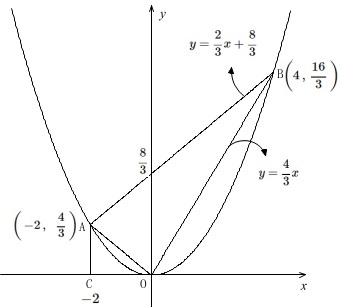問題はここから始まります。

　直線\(\,\mathrm{OB}\,\)上に\(\,\mathrm{D}\,\)、
　直線\(\,\mathrm{AB}\,\)上に\(\,\mathrm{E}\,\)

を\(\,\mathrm{DE}\,\)が\(\,y\,\)軸に平行になるように取ります。

このとき\(\,\mathrm{D}\,\)の\(\,x\,\)座標を\(\,t\,\)とするとき
　\(\,\mathrm{△BED=2△OAC}\,\)
となる\(\,t\,\)を求めます。

点\(\,\mathrm{D}\,\)の\(\,x\,\)座標を\(\,t\,\)とすると
点\(\,\mathrm{D}\,\)は\(\,\mathrm{OB}\,\)上の点なので
　\(\,\displaystyle \mathrm{D}\,\left(\,t\,,\,\frac{4}{3}\,t\,\right)\)
点\(\,\mathrm{E}\,\)は\(\,\mathrm{AB}\,\)上の点なので
　\(\,\displaystyle \mathrm{E}\,\left(\,t\,,\,\frac{2}{3}\,t+\frac{8}{3}\,\right)\,\)

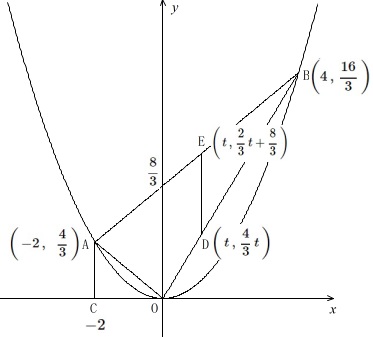必要無いかもしれませんが三角形の面積を表すための情報を書き込んでおきます。
\(\,\mathrm{B}\,\)から直線\(\,\mathrm{DE}\,\)に下ろした垂線の足を\(\,\mathrm{H}\,\)とします。

　\(\begin{eqnarray}\displaystyle
\mathrm{\color{blue}{DE}}&=&\left(\,\frac{2}{3}\,t+\frac{8}{3}\,\right)-\left(\frac{4}{3}\,t\right)\\
&=&\color{blue}{\frac{8}{3}-\frac{2}{3}\,t}
\end{eqnarray}\)

　\(\mathrm{\color{magenta}{BH}}=\color{magenta}{4-t}\)

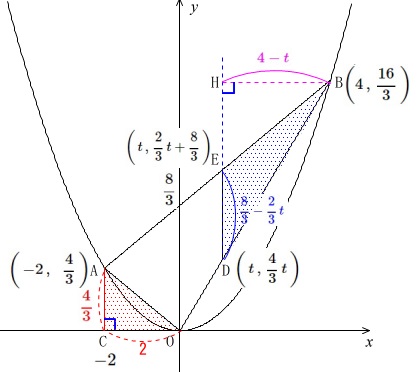　\(\,\mathrm{△BED=2△OAC}\,\)
を方程式にしましょう。

　\(\begin{eqnarray}\displaystyle
△\mathrm{BED}&=&\frac{1}{2}\times \mathrm{\color{blue}{DE}}\times \mathrm{\color{magenta}{BH}}\\
&=&\frac{1}{2}\times \left(\,\frac{8}{3}-\frac{2}{3}\,t\,\right)\times (4-t\,)\\
&=&\frac{1}{2}\times \frac{2}{3}\times (4-t\,)\times (4-t\,)\\
&=&\color{blue}{\frac{1}{3}\,(4-t\,)^2}
\end{eqnarray}\)

　\(\begin{eqnarray}\displaystyle
△\mathrm{OAC}&=&\frac{1}{2}\times \mathrm{\color{red}{AC}}\times \mathrm{\color{red}{OC}}\\
&=&\frac{1}{2}\times \frac{4}{3}\times 2\\
&=&\color{red}{\frac{4}{3}}
\end{eqnarray}\)

より
　\(\begin{eqnarray}\displaystyle
\color{blue}{\frac{1}{3}\,(4-t\,)^2}&=&2\times \color{red}{\frac{4}{3}}\\
(4-t\,)^2&=&8\\
16-8t+t^2&=&8\\
t^2-8t+16-8&=&0\\
t^2-8t+8&=&0
\end{eqnarray}\)

この\(\,2\,\)次方程式は因数分解できないので解の公式です。
　
　\(\begin{eqnarray}\displaystyle
t&=&\frac{-(-8)\pm \sqrt{8^2-4\times (1)\times (8)}}{2\times 1}\\
&=&\frac{8\pm \sqrt{64-32}}{2}\\
&=&\frac{8\pm \sqrt{32}}{2}\\
&=&\frac{8\pm 4\sqrt{2}}{2}\\
&=&4\pm 2\sqrt{2}　
\end{eqnarray}\)

でも良いですが、\(\,\mathrm{C}\,\)問題を受験して高校進学するなら

　\(ax^2+2\color{red}{b’}x+c=0\)
の解は（\(\,x\,\)の\(\,1\,\)次の項の係数が偶数のとき）
　\(\displaystyle x=\frac{-\color{red}{b’}\pm\sqrt{(\color{red}{b’})^2-ac}}{a}\)
は今のうちに覚えておくと良いです。

　\(\begin{eqnarray}\displaystyle
t&=&\frac{4\pm \sqrt{4^2-8}}{1}\\
&=&4\pm \sqrt{8}\\
&=&4\pm 2\sqrt{2}
\end{eqnarray}\)

ここで　\(\,0\,＜\,t\,＜\,4\,\)　なので（問題に書いてあります。）

　\(\,t=\underline{　4-2\sqrt{2}　}\,\)

　\(\,\large{1}\,\)　は以上です。
大阪の上位校を志望するなら1つも落とせませんね。

\(\,\large{2}\,\)は平面図形の角度から相似の証明、面積までの総合問題です。

⇒　2018年(平成30年)度大阪府公立高校入試C問題2平面図形の解説

誘導がしっかりされているので条件を見逃さなければ大丈夫でしょう。

⇒　全国の公立高校入試 数学過去問の解答解説

2019年の問題も大阪府で公開されたら解説しますので確認してください。