2018年(平成30年)度に群馬県で行われた公立高校入試後期の数学問題の解説の続きです。
第2問は反比例の式決定とグラフ、第3問はデータの活用の代表値、第4問は立方体の動点問題です。
どれも基本的な問題ですが、動点問題で途中で関数が変わるときのポイントはおさえておきましょう。
問題は群馬県でも解答とともに公開していくれています。
\(\,\large{2}\,\)
\(\,2\,\)は反比例の関数（式）決定とグラフの問題です。
第2問反比例の式決定とグラフの書き方
(1)反比例の関数を求めます。
反比例を表す関数は必ず
\(\displaystyle y=\frac{a}{x}\)
となるので \(x=-2\,,\,y=2\) を通ることから
\(\begin{eqnarray}\displaystyle
(2)&=&\frac{a}{(-2)}\\
2\times (-2)&=&a\\
-4&=&a
\end{eqnarray}\)
よって
\(\displaystyle \underline{ y=-\frac{4}{x} }\)
または、
\(\displaystyle \underline{ y=\frac{-4}{x} }\)
でも良いですが、分母にマイナスを残すのはやめましょう。
(2)
関数は \(\displaystyle y=-\frac{4}{x}\) と求まっているので、
点をいくつか取ってつなげれば良いだけです。
曲線は点の集まりなので数多くの点を取れば関数のグラフは必ず書けます。
しかし、時間を余りかけたくないので必要最低限にしたいですよね。
比例や\(\,1\,\)次関数の直線は異なる\(\,2\,\)点でいいです。
ただ、この問題の反比例と\(\,y=ax^2\,\)のグラフは、
\(\,x\,\)が整数の値で取れるだけとってつなげるときれいに書けます。
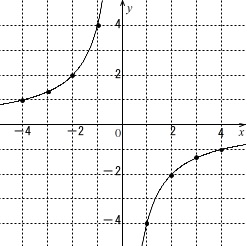このグラフが答えです。
第3問資料（データ）の活用と代表値
\(\,\large{3}\,\)
はくさいの出荷量のデータです。
\(\begin{array}{|c|c|} \hline
都県名 & 出荷量(\mathrm{t}) \\ \hline
茨城県 & 224400 \\ \hline
栃木県 & 18600 \\ \hline
群馬県 & 22300 \\ \hline
埼玉県 & 14000 \\ \hline
千葉県 & 6500 \\ \hline
東京都 & 2840 \\ \hline
神奈川県 & 3420 \\ \hline
\end{array}\)
(1)中央値を求めるにはデータの小さい順か大きい順に並べれば良いです。
順番で真ん中に位置するデータの値が中央値です。
\(\begin{array}{|c|c|} \hline
都県名 & 出荷量(\mathrm{t}) \\ \hline
茨城県 & 224400 \\ \hline
群馬県 & 22300 \\ \hline
栃木県 & 18600 \\ \hline
埼玉県 & \color{red}{14000} \\ \hline
千葉県 & 6500 \\ \hline
神奈川県 & 3420 \\ \hline
東京都 & 2840 \\ \hline
\end{array}\)
答え \(\,\underline{ 14000 (\mathrm{t}) }\,\)
(2)
代表値と平均値がふさわしくない理由を答えるので、平均値は出さなくて良いようです。
例えば、茨城県では、
東京都の\(\,80\,\)倍ぐらい出荷しています。
\(\,2\,\)位の群馬県と比べても\(\,10\,\)倍くらいあります。
このデータで関東\(\,7\,\)県が平均値ほど出荷しているとするには余りにもズレが大きいです。
だから平均値は代表値として適さない、ということを簡単に言えば良いです。
（答え）
茨城県の出荷量が他県に比べ大きすぎるから。
出荷量が値なので、「出荷量の値が」としつこく言う必要もないでしょう。
第4問立体の動点と体積の関係
\(\,\large{4}\,\)
動点問題を苦手にしている人の原因は簡単です。
具体的に試して見るということをしていないからです。
ながめていて答えが出てくる問題はありません。
問題は立方体の底面（上の面）の周上を\(\,2\,\)点が動くときの四面体（三角錐）の体積\(\,y\,\)を時間\(\,x\,\)で表す単純な問題です。
条件を書き出します。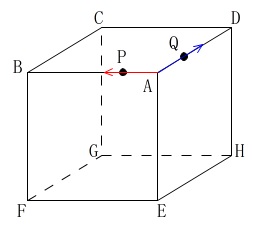
立方体の\(\,1\,\)辺は\(\,6\,\mathrm{cm}\,\)
\(\,\mathrm{P}\,\)は\(\,\mathrm{A}\,\)を出発し、
\(\,\mathrm{B,C,D}\,\)の順に移動して\(\,\mathrm{D}\,\)で止まる。
\(\,\mathrm{P}\,\)の速さは毎秒\(\,\mathrm{1\,cm}\,\)
\(\,\mathrm{Q}\,\)は\(\,\mathrm{A}\,\)を出発し、
\(\,\mathrm{D}\,\)の方向に進み\(\,\mathrm{D}\,\)で止まる。
\(\,\mathrm{Q}\,\)の速さは毎秒\(\,\mathrm{1\,cm}\,\)
\(\,\mathrm{P,Q}\,\)が\(\,\mathrm{A}\,\)を出発してからの時間を\(\,x\,\)
四面体\(\,\mathrm{AEPQ}\,\)の体積は\(\,y\,\)
問題を解いていく前に具体的にいくつか見ておきます。
\(\,\mathrm{P,Q}\,\)の速さが\(\,1\,\)でが\(\,1\,\)辺が\(\,6\,\)なので、
\(\,\mathrm{A}\,\)を出発して\(\,1\,\)辺を動き終えるまでに\(\,6\,\)秒かかります。
例えば、
出発後\(\,3\,\)秒後には\(\,\mathrm{P}\,\)は\(\,\mathrm{AB}\,\)上に、
\(\,\mathrm{Q}\,\)が\(\,\mathrm{AD}\,\)上にあります。
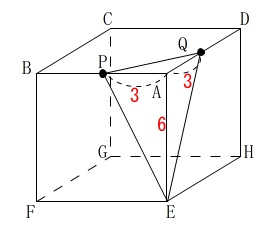\(\,0\,≦\,x\,≦\,6\,\)の場合はこの状態です。
\(\,\mathrm{Q}\,\)は\(\,6\,\)秒後\(\,\mathrm{D}\,\)に到着したら動きません。
\(\,\mathrm{P}\,\)は\(\,6\,\)秒後から\(\,12\,\)秒後までは\(\,\mathrm{BC}\,\)上を動きます。
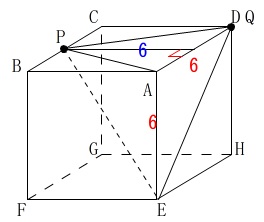\(\,6\,≦\,x\,≦\,12\,\)の場合はこの状態です。
\(\,\mathrm{P}\,\)は\(\,12\,\)秒後からはＣＤ上を動きます。
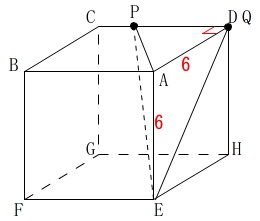\(\,12\,≦\,x\,≦\,18\,\)の場合はこの状態です。
これさえ書き出してイメージできれば答えはすべて出ます。
(1)
\(\,0\,≦\,x\,≦\,6\,\)のときの\(\,x\,\)と\(\,y\,\)の関係です。
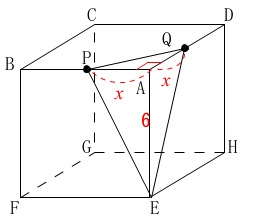\(\,\mathrm{△APQ}\,\)の面積が底面積、\(\,\mathrm{AE}\,\)が高さの三角錐の体積になるので、
\(\begin{eqnarray}\displaystyle
y&=&\frac{1}{3}\times \frac{1}{2}x^2\times 6\\
&=&x^2
\end{eqnarray}\)
答え \(\,\underline{ y=x^2 }\,\)
(2)
\(\,\mathrm{P}\,\)が\(\,\mathrm{BC}\,\)上にあるときは\(\,\mathrm{Q}\,\)は\(\,\mathrm{D}\,\)に止まっています。
このとき底面となる\(\,\mathrm{△APQ}\,\)は底辺と高さが一定なので面積が一定です。
\(\displaystyle △\mathrm{APD}=\frac{1}{2}\times 6\times 6\)
四面体（三角錐）\(\,\mathrm{AEPQ}\,\)の高さも一定なので体積も一定となります。
\(\begin{eqnarray}\displaystyle
y&=&\frac{1}{3}\times △\mathrm{APQ}\times \mathrm{AE}\\
&=&\frac{1}{3}\times \left(\frac{1}{2}\times 6\times 6\,\right)\times 6\\
&=&36
\end{eqnarray}\)
答え \(\,\underline{ ウ （変化しない） }\,\)
この問題は記号だけを答えることになっています。
(4)
\(\,\mathrm{Q}\,\)は\(\,\mathrm{AD}\,\)の間しか動かないので余り考えなくて良いですが、
\(\,\mathrm{P}\,\)は、\(\,\mathrm{A-B}\,\)間、\(\,\mathrm{B-C}\,\)間、\(\,\mathrm{C-D}\,\)間で関数が変わります。
(3)までで\(\,\mathrm{C}\,\)までは関数にしましたので残りの\(\,\mathrm{C-D}\,\)間を関数にすると、
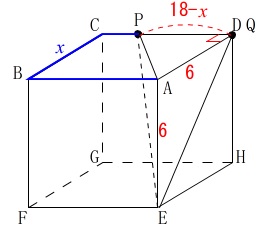\(\,\mathrm{A-B-C-P}\,\)までの時間が\(\,x\,\)で長さも\(\,x\,\)なので、
\(\mathrm{PD}=18-x\)
と表せるので、底面になる\(\,\mathrm{△APD}\,\)の面積は
\(\displaystyle △\mathrm{APD}=\frac{1}{2}\times (18-x)\times 6\)
四面体の体積\(\,y\,\)は
\(\begin{eqnarray}
y&=&\frac{1}{3}\times \frac{1}{2}\times (18-x)\times 6\times 6\\
&=&6(18-x)\\
&=&-6x+108
\end{eqnarray}\)
\(\mathrm{PD}=18-x\,\)は
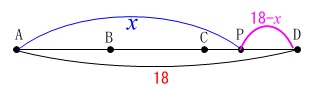直線で考えると分かり易いです。
もう一度まとめて書き出すと
①\(\,0\,≦\,x\,≦\,6\,\)のとき
\(y=x^2 \)
②\(\,6\,≦\,x\,≦\,12\,\)のとき
\(y=36 \)
③\(\,12\,≦\,x\,≦\,18\,\)のとき
\(y=-6x+108 \)
\(\,y=12\,\)となるのは①か③のときしかありません。
①のとき
\(\begin{eqnarray}
12&=&x^2\\
x&=&\pm 2\sqrt{3}
\end{eqnarray}\)
\(\,0\,≦\,x\,≦\,6\,\)を満たすのは
\(\color{red}{x=2\sqrt{3}}\)
③のとき
\(\begin{eqnarray}
12&=&-6x+108\\
6x&=&108-12\\
&=&96\\
\color{red}{x}&\color{red}{=}&\color{red}{16}
\end{eqnarray}\)
これは\(\,12\,≦\,x\,≦\,18\,\)を満たします。
よって答え \(\underline{ x=2\sqrt{3}\,,\,x=16 }\)
答えが1つではないことは問題に『すべて求めなさい。』と書いてあることで分かると思いますが、
①のように適さない値もあるので注意しましょう。
（時間でマイナスはあり得ませんけど。）
調べる範囲が①②③と分かれるのは、
点の動きが変化するときを考え、図を書けばいくつの部分になるかが分かります。
\(\,\large{5}\,\) \(\,\large{6}\,\) もまとめても良かったのですが作業の多い部分になり、長くなるので分けます。
\(\,\large{5},\large{6}\,\)はさいころの確率と半円と接線の問題です。
⇒ 2018年(平成30年)度群馬県公立高校入試の後期数学問題の解説
\(\,\large{1}\,\)は配点が\(\,40\,\)点ある小問集合です。
\(\,\large{2},\large{3},\large{4}\,\)を見てもわかるように基本問題が中心ですので、
教科書レベルの問題を苦手分野をなくして対策しておくことが対策になります。
クラブ活動で忙しい！
塾に通っているのに数学が苦手！
数学の勉強時間を減らしたい！
数学の勉強方法が分からない！
その悩み、『覚え太郎』が解決します！！！
