2018年(平成30年)度に群馬県で行われた公立高校入試後期の数学問題の解説です。
問題1から6までありますが、すごいボリューム、ということはありません。
偏った出題ではありませんので重なる部分も出てきている前期の問題にも目を通しておくと良いですよ。
ここではくどい解説はせずに簡単に済ませておきます。
問題は群馬県でも解答とともに公開していくれています。
\(\,\large{1}\,\)
\(\,1\,\)は小問集合です。
(1)
正負の数と文字式の基本的な計算問題です。
①
\(\hspace{10pt}3+4\times (-2)\\
=3-8\\
=\underline{ -5 }\)
演算の順序を間違えないようにしましょう。
かけ算部分が先です。
②
\(\hspace{10pt}6x^2y\div 2xy\\
\displaystyle =\frac{6x^2y}{2xy}\\
=\underline{ 3x }\)
基本通り「割り算は逆数のかけ算」です。
暗算できない計算ではありませんが、どのような割り算でも同じように計算できるようにしておくと楽ですよ。
③
\(\hspace{10pt}\displaystyle a-\frac{a-3}{2}\\
\displaystyle =\frac{2a-(a-3)}{2}\\
\displaystyle =\frac{2a-a+3}{2}\\
\displaystyle =\underline{ \frac{a+3}{2} }\)
分母を1つにして分子の計算に集中するのがコツです。
分子には（かっこ）がついているので注意して下さい。
(2)
\(\,a\,\)の平方根は\(\,2\,\)乗すると\(\,a\,\)となる数のことです。
\(x^2=a\)
を満たす\(\,x\,\)が\(\,a\,\)の平方根です。
\(x=\pm \sqrt{a}\)
普通だと平方根は2つあります。
ただし、中学の間は\(\,2\,\)乗してマイナスになる数はあつかいません。
さらに、\(\,0\,\)の平方根は\(\,0\,\)です。
意味が違いますので\(\,\color{red}{\pm 0}\,\)としないようにしましょう。
\(\begin{eqnarray}
x^2&=&8\\
x&=&\pm \sqrt{8}\\
&=&\underline{ \pm 2\sqrt{2} }
\end{eqnarray}\)
(3)
与えられた値
\(\,x=2\,,\,y=-3\,\)
を条件式といい、
\(\,2(x-3y)-(3x-5y)\,\)
のような値を求める式を与式、または求値式といいます。
与式、求値式を簡単にしてから最後に条件式を代入します。
最初から代入して算数するのも良いですが、無駄な時間です。
\(\hspace{10pt} 2(x-3y)-(3x-5y)\\
=2x-6y-3x+5y\\
=-x-y\\
=-(2)-(-3)\\
=-2+3\\
=\underline{ 1 }
\)
(4)
展開してから因数分解しても良いですが、
\(\,a-4\,\)
が同じだと主張しているのでまとめ文字にしてから因数分解しておきましょう。
\(\,a-4=\mathrm{A}\,\)とすると
\(\hspace{10pt}(a-4)^2+4(a-4)-12\\
=A^2+4A-12\\
=(A+6)(A-2)\)
\(\,\mathrm{A}\,\)を元に戻して、
\(\hspace{10pt}(A+6)(A-2)\\
=(a-4+6)(a-4-2)\\
=\underline{ (a+2)(a-6) }\)
(5)
直線が平行ということは傾きが同じだということと同じです。
求める直線は
\(y=-3x+b\)
とおけるので\(\,(\,1\,,\,-4\,)\,\)を通ることから代入すると
\(\begin{eqnarray}
(-4)&=&-3\times (1)+b\\
-4&=&-3+b\\
-4+3&=&b\\
-1&=&b
\end{eqnarray}\)
よって求める直線の式は
\(\underline{ y=-3x-1 }\)
(6)
\(\,\mathrm{DE}\, /\!/\,\mathrm{BC}\,\)
なので
\(\,\mathrm{△ADE}\,\) ∽ \(\,\mathrm{△ABC}\,\)
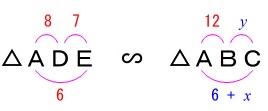相似比から
\(\begin{eqnarray}\displaystyle
8:12&=&6:(6+x)\\
2:3&=&6:(6+x)\\
2(6+x)&=&3\times 6\\
\color{red}{6}+x&=&\frac{3\times 6}{2}\\
x&=&\color{red}{-6}+9\\
&=&\underline{ 3 }
\end{eqnarray}\)
また
\(\begin{eqnarray}\displaystyle
8:7&=&12:y\\
8\times y&=&12\times 7\\
y&=&\frac{12\times 7}{8}\\
&=&\frac{3\times 7}{2}\\
&=&\underline{ \frac{21}{2} }
\end{eqnarray}\)
(8)
円\(\,\mathrm{O}\,\)の周上の点\(\,\mathrm{P}\,\)が\(\,\ell\,\)と一番近くなるときです。
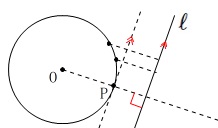中心\(\,\mathrm{O}\,\)と\(\,\ell\,\)との距離は垂線を引けば良いので、
\(\,\mathrm{O}\,\)を通り、\(\,\ell\,\)に垂直な直線と円周との交点が\(\,\mathrm{P}\,\)です。
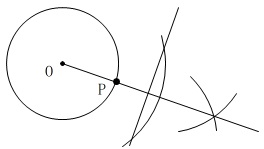
同じ問題をよく見かけますが、
⇒ 作図問題の解き方と入試問題(角の二等分線･垂線･円の接線他)
まとめてありますので苦手な人は確認しておくと良いです。
(9)
文字式の基本問題です。
文字式一覧を覚えている人にとっては簡単な連立方程式の問題ですが、最後に1つ注意点があります。
十の位の数を\(\,x\,\)
一の位の数を\(\,y\,\)
とおいておきます。
十の位と一の位の数の和が\(\,10\,\)
から言える関係式は
\(x+y=10 ･･･①\)
もとの自然数
\(10x+y\)
十の位と一の位の数を入れかえた数
\(10y+x\)
と表せるので、
十の位と一の位を入れかえた自然数「は」、
もとの自然数より\(\,36\,\)大きい。
という関係式は
\(10y+x=10x+y+36 ･･･②\)
①②を連立しますが②を少し簡単にしておきます。
\(\begin{eqnarray}
10y+x&=&10x+y+36\\
10y+x-10x-y&=&36\\
9y-9x&=&36\\
y-x&=&4 ･･･②’
\end{eqnarray}\)
①②’から
\(\hspace{23pt}x+y=10\\
\underline{+)-x+y=\hspace{4pt}4 }\\
\hspace{36pt}2y=14\\
\hspace{42pt}y=7
\)
このとき①に代入して
\(\begin{eqnarray}
x+(7)&=&10\\
x&=&10-7\\
&=&3
\end{eqnarray}\)
この問題はもとの自然数を聞いているのでこれらが答えではありません。
答え \(\,\underline{ 37 }\,\)
②の方程式を立てるとき、
もとの自然数と位を入れかえた数
の関係は、
もとの自然数の方が\(\,36\,\)小さい
ということから
\(10x+y=10y+x\) （← 成立していません。）
とした時点では左辺の方が小さいです。
だから左辺に\(\,+36\,\)すればつり合います。
\(10x+y+36=10y+x\)
関係式を作るのが苦手な人はいったん2つの文字式を並べてみて下さい。
そしてどちらが大きいか、小さいかを問題から判断して、
どちらにいくら加えれば
どちらからいくら引けば
つり合うかを考えると方程式は立てやすくなりますよ。
問題文の「は」は数学の『\(\,=\,\)』と同じだと考えて、問題文の「は」の前後で方程式を立てて見ると良いですね。
\(\,\large{1}\,\)はここまでです。
\(\,\large{2}\,\),\(\,\large{3}\,\)も小問なのですが解説を分けます。
ページを移動するのはめんどうでしょうけど、\(\,\large{1}\,\)だけで\(\,40\,\)点です。
いかに基本が重要とされているか分かりますよね。
\(\,\large{2}\,\)は反比例の関数決定とグラフ。
\(\,\large{3}\,\)は資料の活用の代表値について。
\(\,\large{4}\,\)は立体図形（立方体）の動点問題。
\(\,\large{5}\,\)は確立。
\(\,\large{6}\,\)は平面図形の応用。
と続きます。
前期でも同じですが基本的な問題にちょっと作業をさせているだけのいやらしさのない問題です。
過去問を解けば対策になるということではありませんが、
数年分だけでも過去問に目を通しておくと自ずと対策も見えてきます。
クラブ活動で忙しい！
塾に通っているのに数学が苦手！
数学の勉強時間を減らしたい！
数学の勉強方法が分からない！
その悩み、『覚え太郎』が解決します！！！
