2018年(平成30年)度に群馬県で行われた公立高校入試後期の数学問題の解説の続きです。
第5問はさいころを投げたで目によるビンゴゲームと確率問題、
第6問は2つの半円と接線において長さ、面積を求める平面図形総合問題です。
問題は群馬県でも解答とともに公開していくれています。
\(\,\large{5}\,\)
第5問さいころを投げるときの確率問題
確率問題に限ったことではありませんが問題にはルールがあります。
図形問題だと長さや線分比などの条件として与えられるもののことです。
\(\color{red}{\fbox{\(\,\color{red}{ルール}\,\)}}\)
\(\,1\,\)の目が出たら素数の目を塗りつぶす。
\(\,2\,\)以上の目が出たら出た目の倍数を塗りつぶす。
縦、横、斜めのどれかが\(\,3\,\)マスとも塗りつぶされたら「ビンゴ」
(1)さいころを\(\,1\,\)回投げます。
どの目が出ても塗りつぶされないマスがあるか?
という問題なので出目が\(\,1\,\)から\(\,6\,\)までの場合を調べれば良いだけです。
考えるのではなく調べ尽くせば良いのですよ。
さいころの出目はたった6つです。
出目が\(\,1\,\)のとき塗りつぶすのは素数なので
\(\,2,3,5,7\,\)
出目が\(\,2\,\)のとき塗りつぶすのは偶数なので
\(\,2,4,6,8\,\)
出目が\(\,3\,\)のとき塗りつぶすのは\(\,3\,\)の倍数なので
\(\,3,6,9\,\)
出目が\(\,4\,\)のとき塗りつぶすのは\(\,4\,\)の倍数なので
\(\,4,8\,\)
出目が\(\,5\,\)のとき塗りつぶすのは\(\,5\,\)の倍数なので
\(\,5\,\)
出目が\(\,6\,\)のとき塗りつぶすのは\(\,6\,\)の倍数なので
\(\,6\,\)
表にした方が見やすいかな?
\(\begin{array}{|c|c|} \hline
出目 & 塗りつぶす数字 \\ \hline
1 & 2,3,5,7 \\ \hline
2 & 2,4,6,8 \\ \hline
3 & 3,6,9 \\ \hline
4 & 4,8 \\ \hline
5 & 5 \\ \hline
6 & 6 \\ \hline
\end{array}\)
出てきた数字をBINGO!表に色づけすると
\(\begin{array}{|c|c|c|} \hline
1 & \color{red}{2} & \color{red}{3} \\ \hline
\color{red}{4} & \color{red}{5} & \color{red}{6} \\ \hline
\color{red}{7} & \color{red}{8} & \color{red}{9} \\ \hline
\end{array}\)
これまでに出ていない数字は \(\,\underline{ 1 }\,\) です。
⇒ 素数とは?素因数分解の方法と平方根の求め方(ルートの使い方準備)
\(\,1\,\)は素数ではありません。
(2)
\(\,1\,\)回でビンゴになる確率です。
\(\begin{array}{|c|c|} \hline
出目 & 塗りつぶす数字 \\ \hline
1 & 2,\color{magenta}{3},\color{magenta}{5},\color{magenta}{7} \\ \hline
2 & 2,4,6,8 \\ \hline
3 & \color{magenta}{3},\color{magenta}{6},\color{magenta}{9} \\ \hline
4 & 4,8 \\ \hline
5 & 5 \\ \hline
6 & 6 \\ \hline
\end{array}\)
出目が\(\,1\,\)と\(\,3\,\)のとき
\(\begin{array}{|c|c|c|} \hline
1 & 2 & \color{magenta}{3} \\ \hline
4 & \color{magenta}{5} & \color{magenta}{6} \\ \hline
\color{magenta}{7} & 8 & \color{magenta}{9} \\ \hline
\end{array}\)
ビンゴになります。
答え \(\displaystyle \frac{2}{6}=\underline{ \frac{1}{3} }\)
(3)
\(\,1\,\)回目ではビンゴにならず、\(\,2\,\)回目でビンゴになる確率です。
\(\,1\,\)回目に塗りつぶしたマスは、そのままにしておくので、
\(\,1\,\)回目の\(\,6\,\)通りの出目に対し塗りつぶした後、
\(\,2\,\)回目の出目をルールに従って塗りつぶせば良いだけです。
例えば、
\(\,1\,\)回目に\(\,1\,\)や\(\,3\,\)が出た場合はビンゴになるのでダメです。
また
\(\,1\,\)回目に\(\,1,3\,\)以外が出てビンゴにならなくても、
\(\,2\,\)回目に\(\,1,3\,\)が出た場合は必ずビンゴになります。
\(\,1,3\,\)そのものでビンゴになるので\(\,1\,\)回目は関係ありません。
それ以外にも\(\,2\,\)回目でビンゴになる場合はないか、それを調べれば答えが出ます。
もう一度塗りつぶすルールを確認しておきましょう。
出目が\(\,1\,\)のときは素数、
出目が\(\,2\,\)以上のときは出目の倍数
を塗りつぶします。
\(\,1\,\)回目
\(\,\color{magenta}{1}\,\)のとき
\(\begin{array}{|c|c|c|} \hline
1 & \color{red}{2} & \color{red}{3} \\ \hline
4 & \color{red}{5} & 6 \\ \hline
\color{red}{7} & 8 & 9 \\ \hline
\end{array}\)
ビンゴになるのでダメ。
\(\,\color{magenta}{2}\,\)のとき\(\,2\,\)の倍数を塗りつぶすので
\(\begin{array}{|c|c|c|} \hline
1 & \color{red}{2} & 3 \\ \hline
\color{red}{4} & 5 & \color{red}{6} \\ \hline
7 & \color{red}{8} & 9 \\ \hline
\end{array}\)
\(\,2\,\)回目に\(\,\color{blue}{1}\,\)か\(\,\color{blue}{3}\,\)か\(\,\color{blue}{5}\,\)の目が出ればビンゴになります。
\(\,\color{magenta}{3}\,\)のとき\(\,3\,\)の倍数を塗りつぶすので
\(\begin{array}{|c|c|c|} \hline
1 & 2 & \color{red}{3} \\ \hline
4 & 5 & \color{red}{6} \\ \hline
7 & 8 & \color{red}{9} \\ \hline
\end{array}\)
ビンゴになるのでダメです。
\(\,\color{magenta}{4}\,\)のとき\(\,4\,\)の倍数を塗りつぶすので
\(\begin{array}{|c|c|c|} \hline
1 & 2 & 3 \\ \hline
\color{red}{4} & 5 & 6 \\ \hline
7 & \color{red}{8} & 9 \\ \hline
\end{array}\)
\(\,2\,\)回目に\(\,\color{blue}{1}\,\)か\(\,\color{blue}{3}\,\)の目が出ればビンゴになります。
\(\,\color{magenta}{5}\,\)のとき\(\,5\,\)の倍数を塗りつぶすので
\(\begin{array}{|c|c|c|} \hline
1 & 2 & 3 \\ \hline
4 & \color{red}{5} & 6 \\ \hline
7 & 8 & 9 \\ \hline
\end{array}\)
\(\,2\,\)回目に\(\,\color{blue}{1}\,\)か\(\,\color{blue}{2}\,\)か\(\,\color{blue}{3}\,\)の目が出ればビンゴになります。
\(\,\color{magenta}{6}\,\)のとき\(\,6\,\)の倍数を塗りつぶすので
\(\begin{array}{|c|c|c|} \hline
1 & 2 & 3 \\ \hline
4 & 5 & \color{red}{6} \\ \hline
7 & 8 & 9 \\ \hline
\end{array}\)
\(\,2\,\)回目に\(\,\color{blue}{1}\,\)か\(\,\color{blue}{3}\,\)の目が出ればビンゴになります。
表で見てみると(もちろん樹形図でも良いですよ。)
\(\,1\,\)回目の出目が左端の列の数字、
\(\,2\,\)回目の出目が一番上の行の数字
だとすると
\(\begin{array}{|c|c|c|c|c|c|c|} \hline
& \color{red}{1} & \color{red}{2} & \color{red}{3} & \color{red}{4} & \color{red}{5} & \color{red}{6}\\ \hline
\color{magenta}{1} & × & × & × & × & × & ×\\ \hline
\color{magenta}{2} & ○ & × & ○ & × & ○ & ×\\ \hline
\color{magenta}{3} & × & × & × & × & × & ×\\ \hline
\color{magenta}{4} & ○ & × & ○ & × & × & ×\\ \hline
\color{magenta}{5} & ○ & ○ & ○ & × & × & ×\\ \hline
\color{magenta}{6} & ○ & × & ○ & × & × & ×\\ \hline
\end{array}\)
\(\,36\,\)通りのうち\(\,10\,\)通りが\(\,2\,\)回目でビンゴになるので
答え \(\displaystyle \frac{10}{36}=\underline{ \frac{5}{18} }\)
腕を組んでいても答えは出ないという良い見本です。
第6問半円と接線の平面図形問題
\(\,\large{6}\,\)
半円が2つあり直径の条件がややこしく見えますが、
中心が同じで、半径の違う半円があるというだけです。
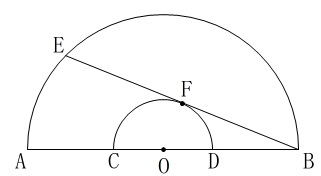 条件を改めて書き出すと、
条件を改めて書き出すと、
\(\,\mathrm{BE}\,\)は接線
\(\,\mathrm{F}\,\)は接点
となっています。
(1)
\(\,\mathrm{△OEF \equiv △OBF}\,\) を証明します。
合同の証明でも相似の証明でも同じですが、ポイントは図の中で証明を終わらせておくことです。
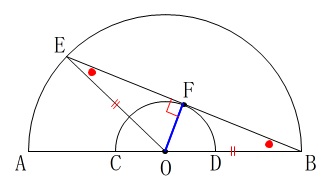 接点と中心を結ぶ半径\(\,\mathrm{OF}\,\)は、接線\(\,\mathrm{BE}\,\)と垂直になるので、
接点と中心を結ぶ半径\(\,\mathrm{OF}\,\)は、接線\(\,\mathrm{BE}\,\)と垂直になるので、
\(\,\mathrm{∠OFE=∠OFB=90^{\circ}} ・・・①\,\)
また、同じ円の半径は常に等しいので
\(\,\mathrm{OE=OB} ・・・②\,\)
このとき\(\,\mathrm{△OFB}\,\)は二等辺三角形なので底角が等しく
\(\,\mathrm{∠OEF=∠OBF} ・・・③\,\)
また、\(\,\mathrm{△OEF}\,\)と\(\,\mathrm{△OBF}\,\)は\(\,\mathrm{OF}\,\)を共有しているので
\(\,\mathrm{OF=OF} ・・・④\,\)
も言えます。
①②③④から合同条件をそろえれば何でも良いです。
直角三角形の斜辺と1つの鋭角
直角三角形の斜辺と他の\(\,1\,\)辺
のどちらかを合同条件にしておけば良いでしょう。
証明は自分でまとめておいて下さい。
注意点としては、直角三角形の合同条件を使って合同を証明するときは
\(\,\mathrm{∠OFE=∠OFB=\color{red}{90^{\circ}}} ・・・①\,\)
の角度が等しいだけではなく、\(\,\color{red}{90°}\,\)までしっかり示しておくことです。
二等辺三角形の頂角の二等分線は底辺を垂直に二等分する。
この定理は逆も言えるので、\(\,\mathrm{∠EOF=∠BOF}\,\)も言えますが遠回りでしょう。
(2)
線分の長さと部分面積を求める問題です。
条件として長さが与えられます。
\(\,\mathrm{AO=6}\,\)
\(\,\mathrm{CO}=a (\,0\,<\,a\,<\,6\,)\)
\(\,0\,<\,a\,<\,6\,\)は小さい円は大きい円をはみ出ることは無いということです。
「大きい円」、「小さい円」と問題に書いてあるので余り深く考えなくて良いです。
①
「\(\,a=2\,\)のときの\(\,\mathrm{BE}\,\)の長さ」
を求めます。
図を書いて長さを書き込めばすぐに答えは出ます。
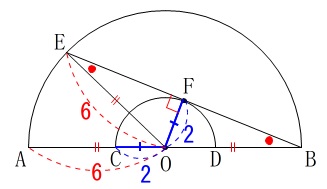 半径は常に等しいので、
半径は常に等しいので、
\(\,\mathrm{OA=\color{red}{OE}}=\color{red}{6}\,\)
\(\,\mathrm{OC=\color{blue}{OF}}=\color{blue}{2}\,\)
直角三角形\(\,\mathrm{△OEF}\,\)に三平方の定理を用いて
\(\begin{eqnarray}
\mathrm{\color{blue}{OF^2}+EF^2}&=&\mathrm{\color{red}{OE^2}}\\
\color{blue}{2^2}+\mathrm{EF^2}&=&\color{red}{6^2}\\
\mathrm{EF^2}&=&6^2-2^2\\
&=&36-4\\
&=&32\\
\mathrm{EF}&=&\pm 4\sqrt{2}
\end{eqnarray}\)
\(\,\mathrm{EF}\,\)は長さなので\(\,\mathrm{EF\,>\,0}\,\)だから
\(\,\mathrm{\color{magenta}{EF}=\color{magenta}{4\sqrt{2}}}\,\)
\(\,\mathrm{BE}\,\)は\(\,\mathrm{EF}\,\)の\(\,2\,\)倍なので
\(\begin{eqnarray}
\mathrm{BE}&=&2\mathrm{\color{magenta}{EF}}\\
&=&2\times \color{magenta}{4\sqrt{2}}\\
&=&\underline{ 8\sqrt{2} }
\end{eqnarray}\)
正負を示す部分はなくても良いです。
答えだけで良いので計算はていねいにやって進めれば短時間で答えは出ますが、ながめているだけでは進みませんよ。
②
「\(\,a=3\,\)のときの\(\,\mathrm{CE}\,\)の長さ」
を求めます。
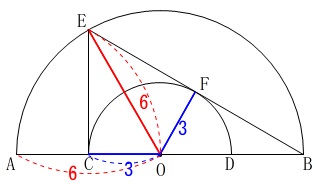 図を長さも正確に書き込むと\(\,\mathrm{△ECB}\,\)は直角三角形に見えますが、
図を長さも正確に書き込むと\(\,\mathrm{△ECB}\,\)は直角三角形に見えますが、
\(\,\mathrm{△ECB}\,\)が直角三角形とは言えていません。
しかし、
\(\,\mathrm{△OEF}\,\)が三角定規の1つの形
であることから、
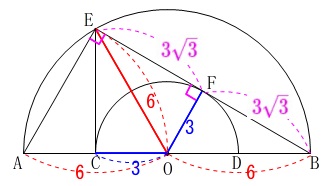
\(\mathrm{\color{magenta}{EF}}=\color{magenta}{3\sqrt{3}}\)
\(\mathrm{\color{blue}{BE}=2\color{magenta}{EF}}=\color{blue}{6\sqrt{3}}\)
また
\(\,\mathrm{△ABE}\,\)が直径\(\,\mathrm{\color{red}{AB}}\,\)を斜辺とする直角三角形
であることから
\(\begin{eqnarray}
\mathrm{AE^2+\color{blue}{BE}^2}&=&\mathrm{\color{red}{AB}^2}\\
\mathrm{AE^2}+(\,\color{blue}{6\sqrt{3}}\,)^2&=&\color{red}{12}^2\\
\mathrm{AE^2}+108&=&144\\
\mathrm{AE^2}&=&144-108\\
&=&36\\
\mathrm{AE}&=&6 (\,\mathrm{AE}\,>\,0\,)
\end{eqnarray}\)
このとき\(\,\mathrm{△OAE}\,\)は正三角形です。
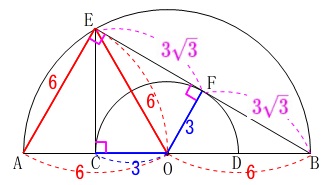
\(\,\mathrm{△OAE}\,\)の底辺を\(\,\mathrm{OA}\,\)としたときの\(\,\mathrm{CE}\,\)はその高さで
\(\,\mathrm{CE}=\underline{ 3\sqrt{3} }\,\)
③
小さい円が2つのあるので\(\,\mathrm{P,Q}\,\)の位置をしっかり書き込みましょう。
\(\,a=\color{blue}{3\sqrt{2}}\,\)のときの\(\,\mathrm{E}\,\)を\(\,\mathrm{P}\,\)
\(\,a=\color{magenta}{3\sqrt{3}}\,\)のときの\(\,\mathrm{E}\,\)を\(\,\mathrm{Q}\,\)
とすると接点と中心を結んだ半径は接線に垂直なので
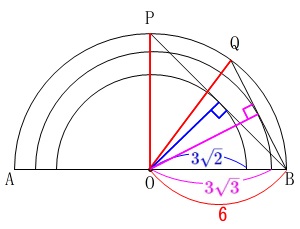 また\(\,\mathrm{OP=OQ=\color{red}{6}}\,\)だから
また\(\,\mathrm{OP=OQ=\color{red}{6}}\,\)だから
接点を図のように\(\,\mathrm{R,S}\,\)とすると
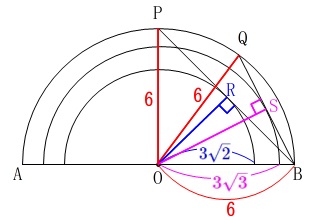
\(\mathrm{OR}=\color{blue}{3\sqrt{2}}\)
\(\mathrm{OS}=\color{magenta}{3\sqrt{3}}\)
であることから三平方の定理を利用して
\(\mathrm{SB=SQ}=3\)
\(\mathrm{RB=RP}=3\sqrt{2}\)
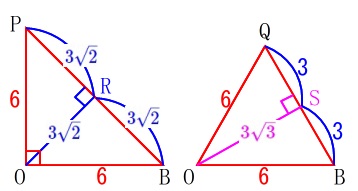
\(\,\mathrm{△OBP}\,\)は直角二等辺三角形
\(\,\mathrm{△OBQ}\,\)は正三角形
であることが分かります。
つまり求める面積は
半径\(\,6\,\)の円の\(\displaystyle \frac{1}{4}\)(四分円)
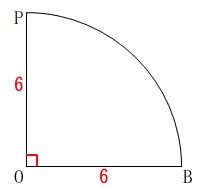
\(\displaystyle \frac{1}{4}\times \pi\,(6^2)=\color{red}{9\pi}\)
から
直角三角形\(\,\mathrm{OBP}\,\)
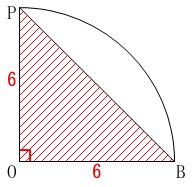
\(\begin{eqnarray}\displaystyle
△\mathrm{OBP}&=&\frac{1}{2}\times 6\times 6\\
&=&\color{blue}{18}
\end{eqnarray}\)
と
中心角\(\,60°\,\)の扇形から正三角形\(\,\mathrm{OBQ}\,\)を引いた
(弦\(\,\mathrm{BQ}\,\)と弧\(\,\mathrm{BQ}\,\)で囲まれた部分)
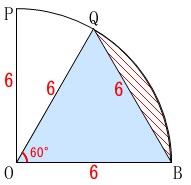
\(\hspace{10pt}\displaystyle \pi (6^2)\times \frac{60}{360}-\frac{1}{2}\times 6\times 3\sqrt{3}\\
=\color{blue}{6\pi-9\sqrt{3}}\)
を引いた面積になります。
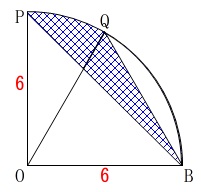
よって求める面積は
\(\hspace{10pt}\color{red}{9\pi}-\color{blue}{18}-(\color{blue}{6\pi-9\sqrt{3}})\\
=9\pi -18-6\pi+9\sqrt{3}\\
=\underline{ 3\pi-18+9\sqrt{3} }\)
2018年度の群馬県公立入試後期の問題は終わりです。
⇒ 2018年(平成30年)度群馬県公立高校入試の後期数学問題の解説
\(\,\large{1}\,\)の小問集合で\(\,40\,\)点
\(\,\large{2}\,\),\(\,\large{3}\,\),\(\,\large{4}\,\)の反比例のグラフ、データの活用の代表値、関数問題で\(\,30\,\)点
それとここにある確率と平面図形で\(\,30\,\)点の配点ですが、
むらなく出題されていることと基本中心であることを知っておくと対策はしやすいでしょう。
2019年度以降の群馬県の数学過去問の問題解説や更新はまとめページで確認しておいて下さい。
