2018(平成30)年度に愛知県で行われた公立高校入試B日程の数学の問題と解説です。
A日程と同様にすべてといって良い程広い範囲からの出題となっています。
応用問題はありますが、基本中心のバランスの良い問題なので中学数学の総復習として参考になります。
問題は愛知県でも公開してくれています。
\(\,\large{1}\,\)は小問集合です。
(1)
\(\hspace{10pt}2\times (-3)+10\\
=-6+10\\
=\underline{ 4 }\)
かけ算割り算が、足し算引き算より先です。
(2)
\(\hspace{10pt}6ab\times (-3ab)^2\div 27ab^2\\
\displaystyle =\frac{6ab\times (-3ab)^2}{27ab^2}\\
\displaystyle =\frac{6ab\times 9a^2b^2}{27ab^2}\\
=\underline{ 2a^2b }\)
割り算は逆数のかけ算なので\(\,\div\,\)の直後を分母に回せば約分するだけです。
(3)
展開公式
\(\,\color{red}{(a+b)^2=a^2+2ab+b^2}\,\)
を利用して、強引に展開してみます。
\(\hspace{10pt}\color{red}{(\sqrt{3}+1)^2}-2(\sqrt{3}+1)\\
=\color{red}{3+2\sqrt{3}+1}-2\sqrt{3}-2\\
=\underline{ 2 }\)
共通因数が見えるので、
\(\hspace{10pt}(\color{blue}{\sqrt{3}+1})^2-2(\color{blue}{\sqrt{3}+1})\\
=(\color{blue}{\sqrt{3}+1})(\sqrt{3}+1-2)\\
=(\sqrt{3}+1)(\sqrt{3}-1)\\
=3-1\\
=\underline{ 2 }\)
展開公式
\(\color{red}{(a+b)(a-b)=a^2-b^2}\)
を利用しました。
どちらも大して変わりませんので、試験会場では思いついた方で突っ走った方がはやいです。
(4)
因数分解の手順はいくつかありますが決まっています。
しかし、高校入試の因数分解はほとんどが公式利用で終わります。
共通因数がないので展開しましょう。
\(\hspace{10pt}(x+1)(x+4)-2(2x+3)\\
=x^2+5x+4-4x-6\\
=x^2+x\color{red}{-2}\)
定数項\(\,\color{red}{-2}\,\)に着目します。
かけて\(\,2\,\)になるのは\(\color{black}{\fbox{ 1×2 }}\)しかないので、
\(\,1\,\)か\(\,2\,\)のどちらかにマイナスをつけて、
足して\(\,x\,\)の\(\,1\,\)次の項の係数\(\,+1\,\)になるのは、
\(\,(-1)+(+2)=+1\,\)
なので
\(\hspace{10pt}x^2+x-2\\
=\underline{ (x+2)(x-1) }\)
すべての因数分解の手順もこの中にあります。
(5)
方程式を解くこととと、方程式の解を求めることは同じです。
方程式を解くときの基本はすべての項を左辺に集めて、右辺を\(\,0\,\)にすることです。
\(\begin{eqnarray}
x(x+1)&=&2(1-x)\\
x(x+1)-2(1-x)&=&0\\
x^2+x-2+2x&=&0\\
x^2+3x-2&=&0
\end{eqnarray}\)
因数分解できないので解の公式です。
\(\begin{eqnarray}\displaystyle
x&=&\frac{-3\pm \sqrt{3^2-4\times 1\times (-2)}}{2}\\
&=&\frac{-3\pm \sqrt{9+8}}{2}\\
&=&\underline{ \frac{-3\pm \sqrt{17}}{2} }
\end{eqnarray}\)
(6)
費用だけを聞かれているので、求める費用を文字でおいて方程式を立てたくなりますが、
人数を文字でおく連立方程式と考えれば簡単に処理できます。
クラスの人数を\(\,x\,\)とし、かかった費用を\(\,y\,\)とすると
「\(\,700\,\)円ずつ集めると\(\,500\,\)円余る予定が、予定より\(\,7500\,\)円多くかかった。」
ということは、
かかった費用は集めたお金より\(\,7000\,\)円大きい、ということなので
\(y=700x+7000 ・・・①\)
「\(\,1\,\)人\(\,200\,\)円追加して集めるとちょうどまかなえた。」
\(\,1\,\)人\(\,900\,\)円集めたらちょうどかかった費用になるので
\(y=900x ・・・②\)
①②を連立すると、左辺は両方\(\,y\,\)なので
\(\begin{eqnarray}
700x+7000&=&900x\\
700x-900x&=&-7000\\
-200x&=&-7000\\
200x&=&7000\\
x&=&35
\end{eqnarray}\)
よってかかった費用は
\(\begin{eqnarray}
y&=&900\times (35)\\
&=&\underline{ 31500 (円) }
\end{eqnarray}\)
連立しなくても求めることはできます。
かかった費用を\(\,x\,\)とすると、
人数は
最初の集めた状態で
\(\displaystyle \frac{x-7000}{700}\)
となり、追加した状態で
\(\displaystyle \frac{x}{900}\)
となりますが、この人数は変化しないので、
\(\begin{eqnarray}\displaystyle
\frac{x-7000}{700}&=&\frac{x}{900}\\
900(x-7000)&=&700x\\
9(x-7000)&=&7x\\
9x-63000&=&7x\\
2x&=&63000\\
x&=&\underline{ 31500 (円)}
\end{eqnarray}\)
としても同じ答えが出ます。
もう一つ、人数\(\,x\,\)とおいて、かかった費用の方程式にすると、
\(700x-500+7500=900x\)
これから人数が求まるので後でかかった費用を出すこともできます。
(連立方程式にしていないだけで最初の方法と同じです。)
文字の指定はないので、どれでも良いですよ。
(7)
変化の割合です。
\(\displaystyle \color{red}{(変化の割合)}=\frac{ \color{blue}{y\,の増加量} }{ \color{magenta}{x\,の増加量} }\)
です。
ただし、\(\,1\,\)次関数の変化の割合は一定で傾きに一致します。
関数\(\,y=ax^2\,\)の\(\,x\,\)が\(\,1\,\)から\(\,3\,\)まで変化したときの変化の割合は
\((\,1\,,\,a\,)\)
\((\,3\,,\,9a\,)\)
から
\((\,x\,の増加量)=(3)-(1)\,=\,\color{magenta}{2}\,\)
\((\,y\,の増加量)=(9a)-(a)\,=\,\color{blue}{8a}\,\)
よって、変化の割合が\(\,1\,\)次関数の傾き\(\,\color{red}{3}\,\)に等しいので
\(\begin{eqnarray}\displaystyle
\frac{\color{blue}{8a}}{\color{magenta}{2}}&=&\color{red}{3}\\
4a&=&3\\
a&=&\underline{ \frac{3}{4} }
\end{eqnarray}\)
\(\,x\,,\,y\,\)の増加量を出すときは、
\(\,2\,\)点を縦に並べた場合\(\,x\,,\,y\,\)座標とも下から上を引く、上から下を引く、
と、どちらかに引く方向を統一しないと変化の割合が逆になるので注意してください。
(8)
玉を同時に\(\,2\,\)個取り出すときの確率です。
玉を同時に取り出すのと一つひとつを\(\,2\,\)回続けて取り出すことは同じことです。
赤球\(\,3\,\)個
白球\(\,2\,\)個
青球\(\,1\,\)個
の合計\(\,6\,\)個から\(\,2\,\)個取りだし、同じ色の玉を取り出す確率を求めます。
\(\,2\,\)個取り出すので組み合わせを書き出しても良いですが、
同じ色の玉の数が違うので確からしさが違ってくることに注意が必要です。
例えば、(赤,赤)と(白,白)という組み合わせで同じ色になる確率は違います。
同じ色の玉があるときは一つひとつを区別すると考えやすいです。
試験の時は「赤」「白」「青」と漢字で書く時間ももったいないので数字に置きかえるとはやいですよ。
赤球\(\,3\,\)個を\(\,\color{red}{1},\color{red}{2},\color{red}{3}\,\)
白球\(\,2\,\)個を\(\,\color{magenta}{4},\color{magenta}{5}\,\)
青球\(\,1\,\)個を\(\,\color{blue}{6}\,\)
とすると、\(\,2\,\)個取り出す取り出し方は、
\(\begin{array}{|c|c|c|} \hline
\color{red}{1} & \color{red}{2} & ○ \\ \hline
\color{red}{1} & \color{red}{3} & ○ \\ \hline
\color{red}{1} & \color{magenta}{4} & \\ \hline
\color{red}{1} & \color{magenta}{5} & \\ \hline
\color{red}{1} & \color{blue}{6} & \\ \hline
\color{red}{2} & \color{red}{3} & ○ \\ \hline
\color{red}{2} & \color{magenta}{4} & \\ \hline
\color{red}{2} & \color{magenta}{5} & \\ \hline
\color{red}{2} & \color{blue}{6} & \\ \hline
\color{red}{3} & \color{magenta}{4} & \\ \hline
\color{red}{3} & \color{magenta}{5} & \\ \hline
\color{red}{3} & \color{blue}{6} & \\ \hline
\color{magenta}{4} & \color{magenta}{5} & ○ \\ \hline
\color{magenta}{4} & \color{blue}{6} & \\ \hline
\color{magenta}{5} & \color{blue}{6} & \\ \hline
\end{array}\)
樹形図にすると逆の並びも出てきますが、\(\,2\,\)倍になるだけなので確率は同じです。
答え \(\displaystyle \underline{ \frac{4}{15} }\)
確率の積が使えるなら、
\(\,2\,\)個とも同じ色になるのは「赤-赤」「白-白」しかないので
\(\,1\,\)個目に赤玉で\(\,2\,\)個目も赤玉である確率は
\(\displaystyle \color{red}{\frac{3}{6}\times \frac{2}{5}}\)
\(\,1\,\)個目に白玉で\(\,2\,\)個目も白玉である確率は
\(\displaystyle \color{blue}{\frac{2}{6}\times \frac{1}{5}}\)
なので求める確率は
\(\hspace{10pt}\displaystyle \color{red}{\frac{3}{6}\times \frac{2}{5}}+\color{blue}{\frac{2}{6}\times \frac{1}{5}}\\
\displaystyle =\frac{6+2}{30}\\
\displaystyle =\underline{ \frac{4}{15} }
\)
と素早く求めても良いですよ。
(9)
相似な図形の線分の長さを求めます。
問題に「相似」とは書いていませんが、\(\,\mathrm{DE\,/\!/\,BC}\,\)という条件からすぐに読み取れます。
条件を読み取り図示します。
\(\,\mathrm{DE\,/\!/\,BC}\,\)
\(\,\mathrm{AD=2}\,\)
\(\,\mathrm{BC=10}\,\)
\(\,\mathrm{DE=4}\,\)
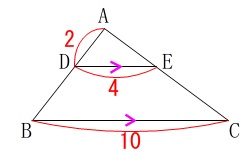 \(\,\mathrm{△ADE}\,\) ∽ \(\,\mathrm{△ABC}\,\)
\(\,\mathrm{△ADE}\,\) ∽ \(\,\mathrm{△ABC}\,\)
なので、\(\,\mathrm{BD}\,\)の長さは直接出ませんが、\(\,\mathrm{AB}\,\)の長さが分かります。
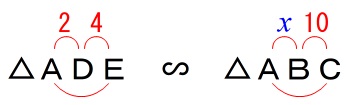
\(\begin{eqnarray}\displaystyle
\mathrm{AD:\color{blue}{AB}}&=&\mathrm{DE:BC}\\
2:\color{blue}{x}&=&4:10\\
4\color{blue}{x}&=&2\times 10\\
\color{blue}{x}&=&\frac{2\times 10}{4}\\
&=&5
\end{eqnarray}\)
\(\,\mathrm{BD=AB-AD}\,\)なので、
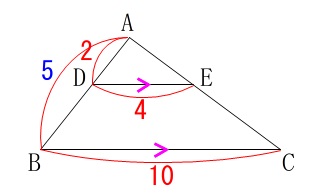
\(\begin{eqnarray}
\mathrm{BD}&=&\color{blue}{5}-\color{red}{2}\\
&=&\underline{ 3 }
\end{eqnarray}\)
相似と比例式の簡単な問題です。
\(\,\large{1}\,\)の小問集合は以上です。
⇒ 2018(平成30年度)愛知県公立高校入試B問題 数学第2問の解説
\(\,\large{2}\,\)も小問集合ですが少し作業量が増えます。
⇒ 愛知県公立高校入試2018(平成30年度)A日程 数学問題の解説(問1)
\(\,\mathrm{A}\,\)日程でも受験するでしょうし、どちらも目を通しておくと良いですね。
広い範囲をまんべんなく問題にしてくれているので過去問を解くだけでも復習になります。
