2018年(平成30年度)愛知県公立高校入試B日程の数学第2問の解説です。
第2問は相似比と体積、データの活用、関数と面積の座標設定問題、動点と長さの関係の関数問題です。
小問集合ではありますが、1問が単独で出題されてもおかしくない作業量となります。
問題は愛知県でも公開してくれています。
\(\,\large{2}\,\)は、(1)から(4)まであります。
相似比と体積比
(1)は相似比と体積比の関係を確認します。
相似な図形は立体でもありますよ。
相似な図形の相似比と面積、体積の関係は
相似比が \(\,\color{red}{a}\,:\,\color{blue}{b}\) のとき
面積比 \(\,\color{red}{a^2}\,:\,\color{blue}{b^2}\,\)
体積比 \(\,\color{red}{a^3}\,:\,\color{blue}{b^3}\,\)
となります。
立体\(\,\mathrm{A}\,\)と\(\,\mathrm{B}\,\)の表面積の比が\(\,16:9\,\)というのは面積比のことです。
面積比が\(\,16:9\,\)
\(\begin{eqnarray}
a^2:b^2&=&16:9\\
&=&4^2:3^2
\end{eqnarray}\)
なので相似比は
\(a:b=4:3\)
よって体積比は
\(\begin{eqnarray}
a^3:b^3&=&4^3:3^3\\
&=&64:27
\end{eqnarray}\)
\(\,\mathrm{A}\,\)の体積は\(\,192 (\mathrm{cm^3})\,\)だから
\(\,\mathrm{B}\,\)の体積を\(\,x\,\)とすると
\(\begin{eqnarray}\displaystyle
64:27&=&192:x\\
64x&=&192\times 27\\
x&=&\frac{192\times 27}{64}\\
&=&\underline{ 81 (\mathrm{cm^3})}
\end{eqnarray}\)
相似は相似比から始めれば良い、という確認です。
範囲と代表値
(2)
データの活用の用語の中でも「範囲」と「代表値」の確認です。
「範囲」とは最大値と最小値の差です。
代表値は「平均値」「中央値」「最頻値（さいひんち）」の3つです。
正しいものをすべて選ぶので、すべて見ていきましょう。
ア
\(\,50\,\)年間の平均値は\(\,25.64\,\)です。（問題に書いてあります。）
そこに\(\,30\,\)という値が1つ増えた\(\,51\,\)年間の平均値は大きくなるはずなので計算するまでもなく、
\(\,\underline{ 正しい。 }\,\)
イ
中央値はデータを順番に並べたときの真ん中の順番になる値のことです。
⇒ 代表値とは？度数分布表の平均値,中央値の求め方と最頻値の答え方
代表値はよく聞かれるので確認しておくと良いです。
データの範囲の中央のことではありません。
このデータでは左から（右からでも同じ）\(\,25\,\)番目と\(\,26\,\)番目の平均となります。
（ちょうど真ん中がないので中央2つの平均を中央値とします。）
だから\(\,50\,\)年間の中央値は\(\,26\,\)日です。
（\(\,25\,\)番目も\(\,26\,\)番目も同じ\(\,26\,\)日にある。）
ウ
\(\,50\,\)年間の中央値は\(\,26\,\)日。
\(\,51\,\)年目の値は\(\,30\,\)日だから度数が\(\,9\,\)になっても、
左右どちらから見ても\(\,26\,\)番目の中央値は\(\,26\,\)日で変わりません。
\(\,\underline{ 正しい。 }\,\)
エ
日数の値は最大値が\(\,31\,\)、最小値が\(\,13\,\)です。
この場合の範囲（レンジ）は
\(\,31-13=18\,\)
です。
オ
\(\,51\,\)年目のデータは\(\,30\,\)日で、\(\,50\,\)年間のデータの最小値と最大値の間に入っているので範囲は変わりません。
\(\,\underline{ 正しい。 }\,\)
カ
最頻値は度数の一番多い値のことです。
もしも度数の最大が2つあれば最頻値は2つになりますが、そんな問題公立高校入試で見たことありません。笑
\(\,51\,\)年目の値は\(\,30\,\)日なので度数が\(\,9\,\)に変わりますが、\(\,26\,\)日の度数は\(\,10\,\)なので
\(\,50\,\)年間の最頻値は\(\,26\,\)日
\(\,51\,\)年間の最頻値も\(\,26\,\)日
と同じです。
\(\,\underline{ 正しい。 }\,\)
答え \(\,\underline{\underline{ ア\,,\,ウ\,,\,オ\,,\,カ }}\,\)
面積を等しくする座標の決定
(3)
平行四辺形と同じ面積になる三角形の頂点を決める問題です。
条件を見ておきます。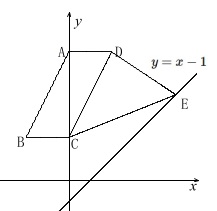
四角形\(\,\mathrm{ABCD}\,\)は平行四辺形
\(\,\mathrm{A,C}\,\)は\(\,y\,\)軸以上の点
\(\,\mathrm{AD}\,\)は\(\,x\,\)軸に平行
\(\,\mathrm{E}\,\)は\(\,y=x-1\,\)上の点
\(\,\mathrm{A}\,\)の座標は\(\,(\,0\,,\,6\,)\,\)
\(\,\mathrm{B}\,\)の座標は\(\,(\,-2\,,\,2\,)\,\)
\(\,\mathrm{E}\,\)の\(\,x\,\)座標は正
分かることは書き込みましょう。
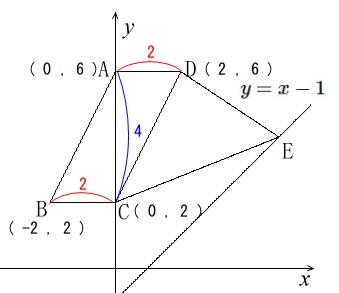平行四辺形\(\,\mathrm{ABCD}\,\)は直角三角形\(\,\mathrm{ABC}\,\)2つ分だから
\(\begin{eqnarray}\displaystyle
\mathrm{ABCD}&=&2\times \frac{1}{2}\times 4\times 2\\
&=&8
\end{eqnarray}\)
なので\(\,\mathrm{△DCE}\,\)の面積が\(\,8\,\)になるときの点\(\,\mathrm{E}\,\)の\(\,x\,\)座標を求めることになります。
『覚え太郎』会員は\(\,\mathrm{E}\,(\,t\,,\,t-1\,)\,\)とおいてダイレクトに求めて良いですよ。
\(\,(\,0\,,\,0\,)\,\) \(\,(\,2\,,\,4\,)\,\) \(\,(\,t\,,\,t-3\,)\,\)
の\(\,3\,\)点で作る三角形の面積と同じなので
\(\begin{eqnarray}\displaystyle
\frac{|2(t-3)-4t|}{2}&=&8\\
|2t-6-4t|&=&16\\
t&=&-11\,,\,5
\end{eqnarray}\)
\(\,\mathrm{E}\,\)の\(\,x\,\)座標は正なので\(\,t=5\,\)だけで、
\(\,\underline{ \mathrm{E}\,(\,5\,,\,4\,) }\,\)
一般向けに教科書の範囲で解いておきます。
点\(\,\mathrm{E}\,\)の\(\,x\,\)座標を\(\,t\,\)とおくと
\(\,\mathrm{E}\,(\,t\,,\,t-1\,)\,\)
ここで\(\,\mathrm{△CDE=8}\,\)を\(\,t\,\)で表すのはややこしくなるので、
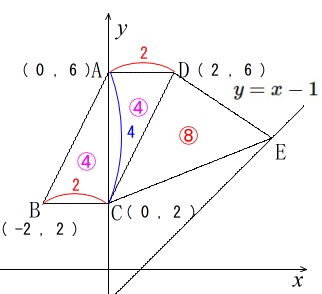
\(\,\mathrm{△ACD=4}\,\)
\(\,\mathrm{△CED=8}\,\)
であることから
\(\,\mathrm{四角形ACED=12}\,\)
を利用します。
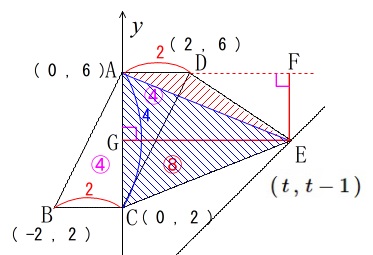
\(\,\mathrm{△ACE}\,\)は底辺\(\,\mathrm{AC}\,\)、高さ\(\,\mathrm{EG}\,\)
\(\,\mathrm{△AED}\,\)は底辺\(\,\mathrm{AD}\,\)、高さ\(\,\mathrm{EF}\,\)
としています。
2つの底辺\(\,\mathrm{AC\,,\,AD}\,\)は\(\,y\,\)座標の差と、\(\,x\,\)座標の差なので
\(\,\mathrm{AC}=\color{blue}{4}\,\)
\(\,\mathrm{AD}=\color{red}{2}\,\)
2つの高さ\(\,\mathrm{EG\,,\,EF}\,\)は\(\,x\,\)座標の差と、\(\,y\,\)座標の差なので
\(\begin{eqnarray}
\mathrm{EG}&=&t-0\\
&=&\color{blue}{t}
\end{eqnarray}\)
\(\begin{eqnarray}
\mathrm{EF}&=&6-(t-1)\\
&=&\color{red}{7-t}
\end{eqnarray}\)
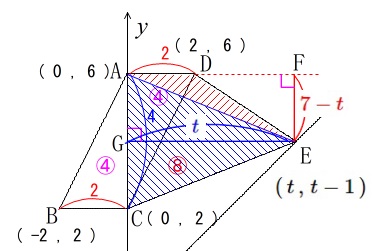よって四角形\(\,\mathrm{ACED}\,\)の面積は\(\,t\,\)を使って
\(\begin{eqnarray}\displaystyle
\mathrm{ACED}&=&\frac{1}{2}\times \color{blue}{4}\times \color{blue}{t}+\frac{1}{2}\times \color{red}{2}\times (\color{red}{7-t})\\
&=&2t+7-t\\
&=&\color{magenta}{t+7}
\end{eqnarray}\)
と表せるので、これが\(\,\color{magenta}{12}\,\)であることから
\(\begin{eqnarray}
\color{magenta}{t+7}&=&\color{magenta}{12}\\
t&=&5
\end{eqnarray}\)
よって求める点\(\,\mathrm{E}\,\)の座標は
\(\,\underline{ \mathrm{E\,(\,5\,,\,4\,)} }\,\)
等積移動が簡単に見つからなかったので具体的な面積を利用しました。
ちなみに、\(\,\mathrm{E}\,\)と\(\,\mathrm{D}\,\)の\(\,y\,\)座標の上下ですが、
\(\,\mathrm{E}\,\)が\(\,\mathrm{D}\,\)と同じ\(\,y\,\)座標のとき、
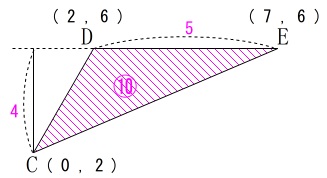
\(\,\mathrm{△CED=10}\,\)
と\(\,\color{red}{8}\,\)より大きくなるので\(\,\mathrm{E}\,\)が\(\,\mathrm{D}\,\)より上になる場合は除外しています。
時間と道のりとグラフ
(4)
動点の問題は変化のある点で場合分けします。
台形\(\,\mathrm{ABCD}\,\)の周上を動きます。
条件を書き出します。
（長さの単位は\(\,\mathrm{m}\,\)で省略します。）
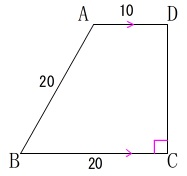
\(\,\mathrm{AD\,/\!/\,BC}\,\)
\(\,\mathrm{AD\,\perp\,DC}\,\)
\(\,\mathrm{AD=10}\,\)
\(\,\mathrm{AB=20}\,\)
\(\,\mathrm{BC=20}\,\)
\(\,\mathrm{D}\,\)を出発して毎秒\(\,5\,\)で\(\,\mathrm{A,B,C}\,\)に向かって移動
移動中で笛が鳴ればその位置から\(\,\mathrm{AD}\,\)と平行に\(\,\mathrm{DC}\,\)に向かって移動
\(\,10\,\)秒以内に笛は鳴る
\(\,\mathrm{AD}\,\)上にいるときは\(\,\mathrm{AD}\,\)上を\(\,\mathrm{D}\,\)まで戻る。
毎秒\(\,5\,\)なので\(\,10\,\)秒後\(\,\mathrm{C}\,\)にいるので\(\,10\,\)秒以内に笛が鳴る、というのは移動途中かちょうど\(\,\mathrm{C}\,\)に到着したときまでに笛が鳴るということがわかります。
変化があるのは点\(\,\mathrm{A,B}\,\)のときなので、\(\,2\,\)秒、\(\,6\,\)秒で場合が分かれるということです。
だから、
\(\,0≦x≦2\,\)
\(\,2≦x≦6\,\)
\(\,6≦x≦10\,\)
の\(\,3\,\)通りが考えられる、という予測はつきます。
①
移動した道のりを計算する具体的な練習問題です。
「\(\,4\,\)秒後に笛がなった。」
速さは毎秒\(\,5\,\)なので\(\,4\,\)秒で\(\,20\,\)進むので
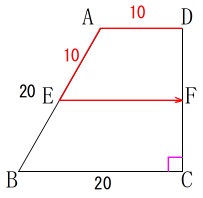\(\,\mathrm{AB}\,\)の中点で\(\,\mathrm{DC}\,\)に向かって移動します。
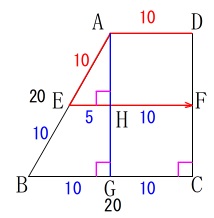中点連結定理から\(\,\mathrm{EH=5}\,\)だから
\(\begin{eqnarray}
\mathrm{EF}&=&\color{blue}{5}+\color{blue}{10}\\
&=&\color{blue}{15}
\end{eqnarray}\)
または、\(\,\mathrm{△ABG}\,\)や\(\,\mathrm{△AEH}\,\)は三角定規の比を利用しても良いです。
よって\(\,\mathrm{D}\,\)を出発してから移動した道のりは
\(\hspace{10pt}\mathrm{DA+AE+EF}\\
=\color{red}{10}+\color{red}{10}+\color{blue}{15}\\
=\underline{ 35 (\mathrm{m})}\)
\(\,\mathrm{EF}\,\)の長さは、
\(\begin{eqnarray}\displaystyle
\mathrm{EF}&=&\frac{\mathrm{AD+BC}}{2}\\
&=&\frac{10+20}{2}\\
&=&\color{blue}{15}
\end{eqnarray}\)
としても良いですよ。
②
出発してからの時間を\(\,x\,\)、移動した道のりを\(\,y\,\)としたときの関係をグラフにします。
\(\,\mathrm{D}\,\)から\(\,\mathrm{A}\,\)までの\(\,2\,\)秒間、
つまり、\(\,\color{red}{0≦x≦2}\,\) のとき、
\(\,\mathrm{AD}\,\)上にいる状態で\(\,\mathrm{DC}\,\)に戻ります。
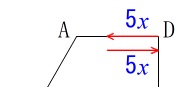\(\,x\,\)秒で\(\,5x\,\)進むので、\(\,\mathrm{DC}\,\)に向けても\(\,5x\,\)移動するから
\(\begin{eqnarray}
y&=&\color{blue}{5x}+\color{blue}{5x}\\
&=&10x (\,0≦x≦2\,)
\end{eqnarray}\)
\(\,\mathrm{A}\,\)から\(\,\mathrm{B}\,\)にいる\(\,4\,\)秒間、
つまり、\(\,\color{red}{2≦x≦6}\,\) のとき
\(\,\mathrm{AB}\,\)上にいる状態で\(\,\mathrm{DC}\,\)に戻ります。
\(\,x\,\)秒で\(\,5x\,\)進むので、\(\,\mathrm{AD=10}\,\)なので
\(\,\mathrm{AI}=\color{red}{5x-10}\,\)
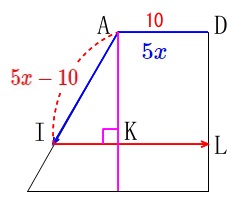①からも分かるように\(\,\mathrm{△AIK}\,\)は三角定規なので
\(\begin{eqnarray}\displaystyle
\mathrm{IK}&=&\frac{1}{2}\,\mathrm{AI}\\
&=&\color{magenta}{\frac{5x-10}{2}}
\end{eqnarray}\)
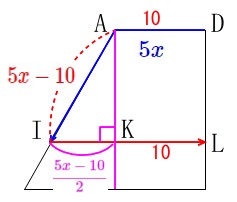移動した道のりは、
\(\begin{eqnarray}\displaystyle
y&=&\color{blue}{5x}+\color{magenta}{\frac{5x-10}{2}}+\color{red}{10}\\
&=&\frac{15}{2}x+5 (2≦x≦6)
\end{eqnarray}\)
\(\,\mathrm{B}\,\)から\(\,\mathrm{C}\,\)にいる\(\,4\,\)秒間、
つまり、\(\,\color{red}{6≦x≦10}\,\) のとき、
この間では結局は
\(\,\mathrm{D\rightarrow A \rightarrow B \rightarrow C}\,\)
と動くことになるのでこの間は移動する道のりは一定で
\(\begin{eqnarray}
y&=&10+20+20\\
&=&50 （6≦x≦10)
\end{eqnarray}\)
グラフにすると
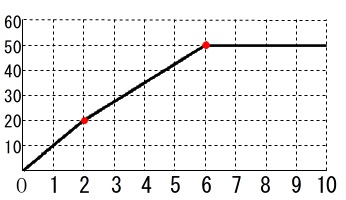となります。
関数を求めてグラフを書きましたが、
\(\,\mathrm{A}\,\)にいるときの時間と移動した道のり
\((\,2\,,\,20\,)\)
\(\,\mathrm{B}\,\)にいるときの時間と移動した道のり
\((\,6\,,\,50\,)\)
\(\,\mathrm{C}\,\)にいるときの時間と移動した道のり
\((\,10\,,\,50\,)\)
を座標として、線分で結んでもグラフは書けます。
\(\,\large{2}\,\)は以上です。
⇒ 2018(平成30年度)愛知県公立高校入試B問題 数学第3問の解説
\(\,\large{3}\,\)は図形総合です。
一点だけ注意したい線分比がありますが、基本中心で組み立てられた応用問題です。
⇒ 2018(平成30)年度愛知県公立高校入試B問題 数学の解説
\(\,\large{1}\,\)は小問集合でした。
⇒ 愛知県公立高校入試2018(平成30年度)A日程 数学問題の解説(問1)
\(\,\mathrm{A}\,\)日程と全体の問題構成は同じです。
クラブ活動で忙しい！
塾に通っているのに数学が苦手！
数学の勉強時間を減らしたい！
数学の勉強方法が分からない！
その悩み、『覚え太郎』が解決します！！！
