2018年(平成30年度)愛知県で行われた公立高校入試B問題の数学第3問の解説です。
第3問は図形総合問題で、円周角の定理、相似な図形、球の表面積と三角柱の体積が問われます。
基本中心なので順序よく処理すればそれほど時間がかかる問題はありません。
問題は愛知県でも公開してくれています。
\(\,\large{3}\,\)は、(1)から(3)までありすべて図形問題です。
円周角の定理の確認問題
(1)
\(\,\mathrm{A,B,C,D}\,\)が同一円周上の点なので円周角が等しいところに注目すれば非常に簡単な問題です。
条件
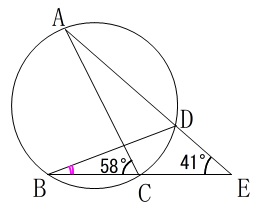
\(\,\mathrm{A,B,C,D}\,\)が円周上の点
\(\,\mathrm{∠ABC=58^{\circ}}\,\)
\(\,\mathrm{∠DEC=41^{\circ}}\,\)
\(\,\mathrm{A,B,C,D}\,\)が円周上の点なので、
\(\,\mathrm{\color{magenta}{∠DBC}=\color{red}{∠DAC}}\,\)
よって\(\,\mathrm{∠DAC}\,\)を求めればいい、とすり替えができます。
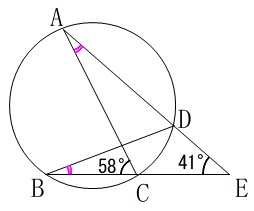
\(\begin{eqnarray}
\mathrm{∠ACB}&=&\mathrm{\color{red}{∠DAC}+∠CEA}\\
58^{\circ}&=&\mathrm{\color{red}{∠DAC}}+41^{\circ}\\
\mathrm{\color{red}{∠DAC}}&=&58^{\circ}-41^{\circ}\\
&=&\underline{ 17^{\circ} }
\end{eqnarray}\)
\(\,\mathrm{∠DBC}\,\)そのものも円周角の定理からすぐに求まります。
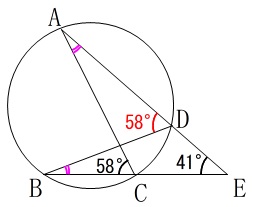
どちらかというと
\(\,\mathrm{∠ACB=\color{red}{∠ADB}=58^{\circ}}\,\)
から
\(\begin{eqnarray}
\mathrm{\color{red}{∠ADB}}&=&\mathrm{∠DEB+\color{magenta}{∠DBC}}\\
\color{red}{58^{\circ}}&=&41^{\circ}+\mathrm{\color{magenta}{∠DBC}}\\
\mathrm{\color{magenta}{∠DBC}}&=&\color{red}{58^{\circ}}-41^{\circ}\\
&=&\underline{ 17^{\circ} }
\end{eqnarray}\)
とする方が自然かもしれません。
相似な図形の線分と面積比
(2)
長方形の中にある相似な図形の長さと面積比を求めます。
図形の条件を書き込みます。
四角形\(\,\mathrm{ABCD}\,\)は長方形
\(\,\mathrm{EF ⊥ AC}\,\)
\(\,\mathrm{EG ⊥ BC}\,\)
\(\,\mathrm{AB=4}\,\)
\(\,\mathrm{AD=6}\,\)
\(\,\mathrm{AE=4}\,\)
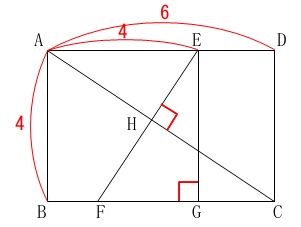 長方形は平行四辺形であり、4つの角は\(\,90°\,\)なので、
長方形は平行四辺形であり、4つの角は\(\,90°\,\)なので、
相似な直角三角形がいろいろ出てきます。
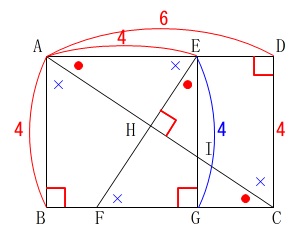
①\(\,\mathrm{FG}\,\)の長さを求めるので選ぶ相似な三角形は\(\,\mathrm{FG}\,\)を\(\,1\,\)辺に持つ
\(\,\mathrm{△ADC}\,\) ∽ \(\,\mathrm{△EGF}\,\)
にしましょう。
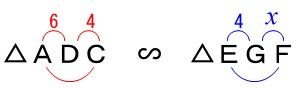 \(\,\mathrm{FG}=x\,\)とすると比例式は
\(\,\mathrm{FG}=x\,\)とすると比例式は
\(\begin{eqnarray}
\mathrm{AD:EG}&=&\mathrm{DC:GF}\\
\color{red}{6}:\color{blue}{4}&=&\color{red}{4}:\color{blue}{x}
\end{eqnarray}\)
これを解いて
\(\begin{eqnarray}\displaystyle
6:4&=&4:x\\
6x&=&4\times 4\\
x&=&\frac{4\times 4}{6}\\
\mathrm{FG}&=&\underline{ \frac{8}{3} (\mathrm{cm})}
\end{eqnarray}\)
②
四角形\(\,\mathrm{HFGI}\,\)と長方形\(\,\mathrm{ABCD}\,\)の面積比です。
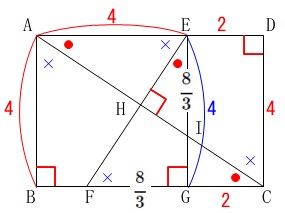 四角形\(\,\mathrm{HFGI}\,\)の面積は公式通りで直接は求まりません。
四角形\(\,\mathrm{HFGI}\,\)の面積は公式通りで直接は求まりません。
公式を使えない面積は
「部分」+「部分」
または
「全体」-「部分」
ですね。
ここでは三角形\(\,\mathrm{EFG}\,\)から三角形\(\,\mathrm{EHI}\,\)を引けば出ます。
\(\,\mathrm{△EFG}\,\)と\(\,\mathrm{△AIE}\,\)は合同なので\(\,\mathrm{△AIE}\,\)から引いても同じです。
\(\,\mathrm{△EHI}\,\)の面積も求め方はいろいろあります。
三平方の定理を使っていないので長さを求めて具体的に出してみましょう。笑
\(\,\mathrm{△ADC}\,\) ∽ \(\,\mathrm{△EHI}\,\)
辺の比が
\(\,\mathrm{AD:DC=6:4=3:2}\,\)
なので
\(\,\mathrm{HI}=\color{magenta}{2x}\,,\,\mathrm{EH}=\color{magenta}{3x}\,\)
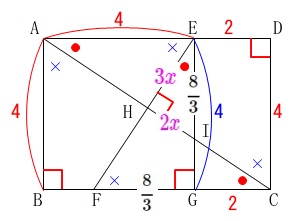
とおくことができて、三平方の定理から
\(\begin{eqnarray}\displaystyle
\mathrm{HI^2}+\mathrm{EH^2}&=&\left(\frac{8}{3}\right)^2\\
(2x)^2+(3x)^2&=&\left(\frac{8}{3}\right)^2\\
4x^2+9x^2&=&\left(\frac{8}{3}\right)^2\\
13x^2&=&\left(\frac{8}{3}\right)^2\\
x^2&=&\left(\frac{8}{3}\right)^2\times \frac{1}{13}\\
\end{eqnarray}\)
\(\,x>0\,\)なので
\(\begin{eqnarray}\displaystyle
x&=&\frac{8}{3}\times \frac{1}{\sqrt{13}}\\
&=&\frac{8}{3}\times \frac{\sqrt{13}}{13}\\
&=&\frac{8\sqrt{13}}{39}
\end{eqnarray}\)
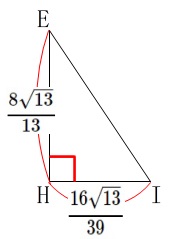
これで底辺と高さが出ます。
\(\begin{eqnarray}\displaystyle
\mathrm{HI}&=&2x\\
&=&2\times \frac{8\sqrt{13}}{39}\\
&=&\frac{16\sqrt{13}}{39}
\end{eqnarray}\)
\(\begin{eqnarray}\displaystyle
\mathrm{EH}&=&3x\\
&=&3\times \frac{8\sqrt{13}}{39}\\
&=&\frac{24\sqrt{13}}{39}\\
&=&\frac{8\sqrt{13}}{13}
\end{eqnarray}\)
 よって
よって
\(\begin{eqnarray}\displaystyle
\mathrm{△EHI}&=&\frac{1}{2}\times \frac{16\sqrt{13}}{39}\times \frac{8\sqrt{13}}{13}\\
&=&\color{blue}{\frac{64}{39}}
\end{eqnarray}\)
 また\(\,\mathrm{△EFG}\,\)は底辺と高さが分かっています。
また\(\,\mathrm{△EFG}\,\)は底辺と高さが分かっています。
\(\begin{eqnarray}\displaystyle
\mathrm{△EFG}&=&\frac{1}{2}\times \mathrm{FG}\times \mathrm{EG}\\
&=&\frac{1}{2}\times \frac{8}{3}\times 4\\
&=&\color{magenta}{\frac{16}{3}}\\
\end{eqnarray}\)
これで四角形の面積が求まります。
\(\begin{eqnarray}\displaystyle
四角形\mathrm{HFGI}&=&\mathrm{\color{magenta}{△EFG}-\color{blue}{△EHI}}\\
&=&\color{magenta}{\frac{16}{3}}-\color{blue}{\frac{64}{39}}\\
&=&\frac{16\times 13-64}{39}\\
&=&\frac{208-64}{39}\\
&=&\frac{144}{39}\\
&=&\frac{48}{13}
\end{eqnarray}\)
長方形\(\,\mathrm{ABCD}\,\)の面積は\(\,24\,\)なので
\(\hspace{10pt}\displaystyle \frac{48}{13}\div 24\\
\displaystyle =\frac{48}{13}\times \frac{1}{24}\\
\displaystyle =\underline{ \frac{2}{13} 倍 }\)
と強引に出してみました。笑笑
『超え太郎』までやっている人はもっと簡単に出して良いですよ。
\(\begin{eqnarray}\displaystyle
\mathrm{FC}&=&\frac{8}{3}+2\\
&=&\color{red}{\frac{14}{3}}
\end{eqnarray}\)
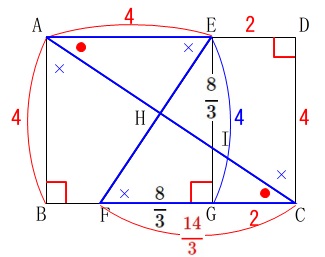 なので
なので
\(\,\mathrm{△AHE}\,\) ∽ \(\,\mathrm{△CHF}\,\)
であることから
\(\begin{eqnarray}\displaystyle
\mathrm{\color{blue}{EH:HF}}&=&\color{red}{4:\frac{14}{3}}\\
&=&\color{blue}{6:7}
\end{eqnarray}\)
また
\(\begin{eqnarray}\displaystyle
\mathrm{\color{red}{EI:IG}}&=&\frac{8}{3}:\frac{4}{3}\\
&=&\color{red}{2:1}
\end{eqnarray}\)
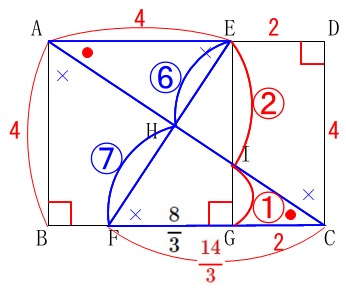 よって(『超え太郎』-「相似な図形」No.60参照)
よって(『超え太郎』-「相似な図形」No.60参照)
\(\begin{eqnarray}\displaystyle
\mathrm{△EHI}&=&\color{red}{\frac{2}{3}}\times \color{blue}{\frac{6}{13}}\times \mathrm{△EFG}\\
&=&\color{magenta}{\frac{12}{13}}\times \frac{1}{2}\times \frac{8}{3}\times 4\\
&=&\frac{64}{39}
\end{eqnarray}\)
と、比を利用しても良いですし、面積を数値で出さずに比のままで処理しても良いです。
しかし、長方形の面積がわかるので具体的に計算する方が分かり易いでしょう。
この問題では使わなくても答えは出てきますが、
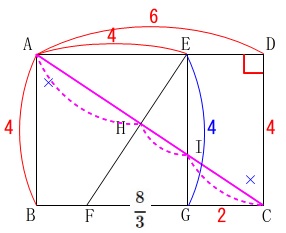 \(\,\mathrm{\color{magenta}{AH:HI:IC}}\,\)の線分比は求められるようになっておきたいところです。
\(\,\mathrm{\color{magenta}{AH:HI:IC}}\,\)の線分比は求められるようになっておきたいところです。
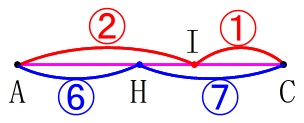 を利用して求まるのでチャレンジしてみてください。
を利用して求まるのでチャレンジしてみてください。
分かり易いのは
\(\,\color{red}{②+①=③}\,\)
\(\,\color{blue}{⑥+⑦=⑬}\,\)
の最小公倍数\(\,39\,\)を\(\,\mathrm{AC}\,\)の長さとして、
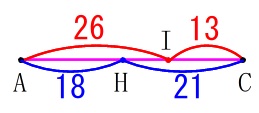 \(\,39\,\)を分けた比にすれば
\(\,39\,\)を分けた比にすれば
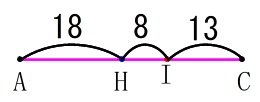 実際の長さではありませんが整数比が出せます。
実際の長さではありませんが整数比が出せます。
この比を使えば三平方の定理は使わなくても面積比は出ます。
球の表面積と三角柱の体積
(3)
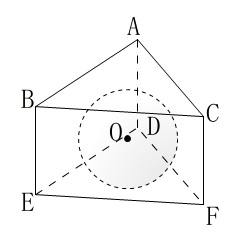
球がきれいに収まった正三角柱です。
①
球の半径は\(\,2\,\)なので表面積は公式で求めます。
半径\(\,r\,\)の球の表面積\(\,S\,\)を求める公式は
\(\color{red}{S=4\,\pi\,r^2}\)
中学生は公式でしか球の表面積や体積を求めることはできません。
球\(\,\mathrm{O}\,\)の半径の\(\,\color{red}{r=2}\,\)を代入して求める表面積は、
\(\hspace{10pt}4\,\pi\,(2)^2\\
=\underline{ 16\pi } (\mathrm{cm^2})\)
②
正三角柱の体積です。
底面は正三角形なのですが、辺の長さは出ていません。
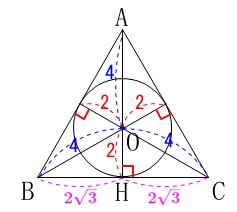
球が各面に接していることから、真上から見ると正三角形に円が接している状態で、
三角定規の比から
\(\mathrm{AO}=\color{blue}{4}\)
から高さとなる
\(\mathrm{AH}=\color{blue}{4}+\color{red}{2}=6\)
また
\(\mathrm{BH=CH}=\color{magenta}{2\sqrt{3}}\)
から底辺となる
\(\,\mathrm{AC}=\color{magenta}{2\sqrt{3}}+\color{magenta}{2\sqrt{3}}=4\sqrt{3}\,\)
 よって底面積は
よって底面積は
\(\begin{eqnarray}
\mathrm{△ABC}&=&\frac{1}{2}\times 4\sqrt{3}\times 6\\
&=&\color{red}{12\sqrt{3}}
\end{eqnarray}\)
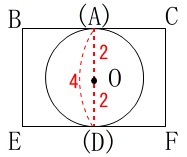
三角柱の高さは球の直径\(\,\color{red}{4}\,\)になるので
(図は\(\,\mathrm{BCFE}\,\)を正面から見た図)
 求める体積は
求める体積は
\(\hspace{10pt}\color{red}{12\sqrt{3}}\times \color{red}{4}\\
=\underline{ 48\sqrt{3} } (\mathrm{cm^3})\)
\(\,2018\,\)年愛知県\(\,\mathrm{B}\,\)日程数学問題は以上です。
⇒ 2018(平成30)年度愛知県公立高校入試B問題 数学の解説
\(\,\large{1}\,\)から見てみるとわかりますが、偏りのない出題となっています。
基本を中心に中学\(\,3\,\)年間の数学をまんべんなく復習しておくことが対策になります。
⇒ 愛知県公立高校入試2018(平成30年度)A日程 数学問題の解説(問1)
\(\,\mathrm{A}\,\)日程も同様です。
同じ問題は出ませんが、分量や難易度はそれほど変化しているわけではありません。
