大阪府公立高校入試2019年(平成31年)度の数学C問題第2問の解説

2019年(平成31年)度に大阪府で行われた公立高校入試の数学C問題の第2問の解説です。
問2は合同、相似な図形の基本から応用まで平面図形の総合問題です。
応用問題はありますがしっかりと条件を抜き出せばそれほど時間のかかる問題ではありません。

問題は大阪府で公開してくれています。

⇒　2019年大阪府C問題

2.平面図形の総合問題

　\(\,\large{2}\,\)　は平面図形の総合で、弧の長さ、証明、線分の長さ、面積とあります。

ダラダラ説明しても長くなりますのでちゃちゃっとかたづけてしまいましょう。笑

図の条件です。

　直径が\(\,\mathrm{BC=8}\,\)の円\(\,\mathrm{O}\,\)がある。
　\(\,\mathrm{ＣＤ=ＣＡ}\,\)となる直線\(\,\mathrm{BC}\,\)上の点を\(\,\mathrm{D}\,\)とする。

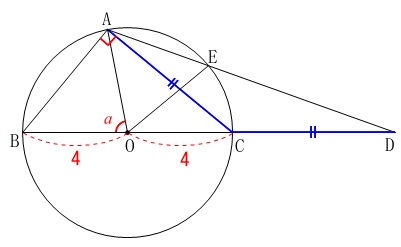
中心角と弧の長さの関係

(1)
\(\,\mathrm{∠AOB}=a\,\)とするとき\(\,\mathrm{\stackrel{\frown}{\mbox{AB}}}\,\)の長さを求めます。

比例式ですね。

　\(\begin{eqnarray}\displaystyle
360:8\,\pi&=&a:\mathrm{\stackrel{\frown}{\mbox{AB}}}\\
360\times \mathrm{\stackrel{\frown}{\mbox{AB}}}&=&a\times 8\pi\\
\mathrm{\stackrel{\frown}{\mbox{AB}}}&=&\frac{8a\,\pi}{360}\\
&=&\underline{　\frac{a\,\pi}{45}　}
\end{eqnarray}\)

比例計算になれているなら

　\(\begin{eqnarray}\displaystyle
\mathrm{\stackrel{\frown}{\mbox{AB}}}&=&8\,\pi\times \frac{a}{360}\\
&=&\underline{　\frac{a\,\pi}{45}　(\mathrm{cm})}
\end{eqnarray}\)

の方がはやいです。

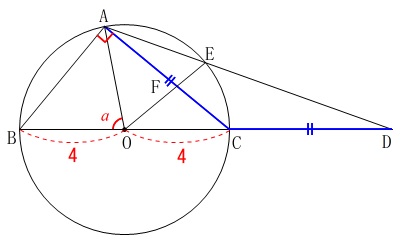
2つの辺の長さが等しいことの証明

(2)
\(\,\mathrm{AC}\,\)と\(\,\mathrm{EO}\,\)の交点をFとしたとき、\(\,\mathrm{FO=FC}\,\)を証明します。

合同か二等辺三角形でしょうか。
分かることを図に書き込んで行きましょう。
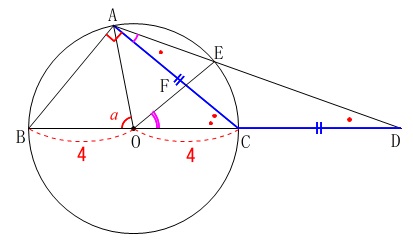見えてきました。

（証明）
中心角は円周角の\(\,2\,\)倍だから

　\(\,\mathrm{∠EOC=2∠EAC}\,　･･･①\)

また、\(\,\mathrm{△CAD}\,\)は二等辺三角形で

　\(\,\mathrm{∠CAD=∠CDA}\,\)

このとき、

　\(\,\mathrm{∠ACO=∠CAD＋∠CDA}\,\)

なので、

　\(\,\mathrm{∠FOC=2∠CAE}\,　･･･②\)

①②より底角が等しいので\(\,\mathrm{△FOC}\,\)は二等辺三角形となり、

　\(\,\mathrm{FO=FC}\,\)　（証明終わり）

二等辺三角形の底角は等しいという定理の逆ですね。

辺の長さと面積の求め方

(3)
条件が加わります。

　\(\,\mathrm{AC=\color{blue}{6}}\,\)
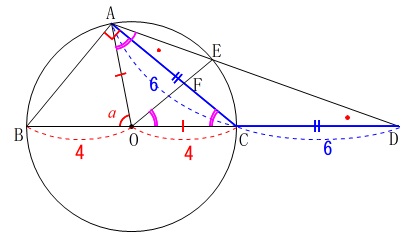①
このとき\(\,\mathrm{OA=OC}\,\)（半径）なので\(\,\mathrm{△OAC}\,\)も二等辺三角形で、
\(\,\mathrm{∠OCF}\,\)と\(\,\mathrm{∠ACO}\,\)は同じ角を示しているので、

　\(\,\mathrm{△FOC}\,\)　∽　\(\,\mathrm{△OAC}\,\)

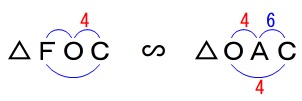
　\(\begin{eqnarray}\displaystyle
\mathrm{FC:OC}&=&\mathrm{OC:AC}\\
\mathrm{FC}:4&=&4:6\\
6\times \mathrm{FC}&=&4\times 4\\
\mathrm{FC}&=&\frac{4\times 4}{6}\\
&=&\underline{　\frac{8}{3}　(\mathrm{cm})}
\end{eqnarray}\)

②
\(\,\mathrm{△AOF}\,\)の面積を求めます。

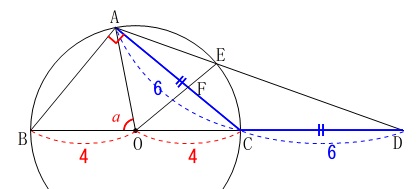
面積を求めることができる、最初に気がつくのは直角三角形\(\,\mathrm{△ABC}\,\)です。

\(\,\mathrm{△ABC}\,\)は直角三角形なので三平方の定理から

　\(\begin{eqnarray}
\mathrm{AB^2+AC^2}&=&\mathrm{BC^2}\\
\mathrm{AB}^2+6^2&=&8^2\\
\mathrm{AB}^2&=&64-36\\
&=&28\\
\mathrm{AB}&=&\color{red}{2\sqrt{7}}
\end{eqnarray}\)
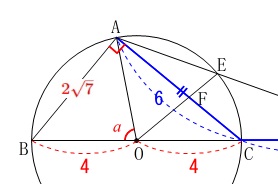よって\(\,\mathrm{△ABC}\,\)の面積を基準に考えましょう。

　\(\begin{eqnarray}\displaystyle
\mathrm{△ABC}&=&\frac{1}{2}\times \color{blue}{6}\times \color{red}{2\sqrt{7}}\\
&=&6\sqrt{7}
\end{eqnarray}\)

\(\,\mathrm{△OAC}\,\)は\(\,\mathrm{△ABC}\,\)の半分なので

　\(\begin{eqnarray}\displaystyle
\mathrm{\color{magenta}{△OAC}}&=&\frac{1}{2}\times 6\sqrt{7}\\
&=&\color{magenta}{3\sqrt{7}}
\end{eqnarray}\)

ここで①で求めた\(\,\mathrm{FC}\,\)より

　\(\begin{eqnarray}\displaystyle
\mathrm{\color{blue}{AF}}&=&\mathrm{AC-\color{red}{FC}}\\
&=&6-\color{red}{\frac{8}{3}}\\
&=&\color{blue}{\frac{10}{3}}
\end{eqnarray}\)

このことから

　\(\begin{eqnarray}\displaystyle
\mathrm{\color{blue}{AF}:\color{red}{FC}}&=&\color{blue}{\frac{10}{3}}:\color{red}{\frac{8}{3}}\\
&=&5:4
\end{eqnarray}\)
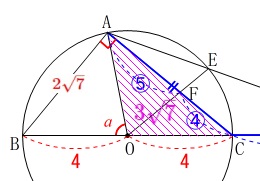よって
　
　\(\begin{eqnarray}\displaystyle
\mathrm{△AOF}&=&\frac{5}{9}\times \mathrm{\color{magenta}{△OAC}}\\
&=&\frac{5}{9}\times \color{magenta}{3\sqrt{7}}\\
&=&\underline{　\frac{5\sqrt{7}}{3}　(\mathrm{cm^2})}
\end{eqnarray}\)
　
\(\,\large{2}\,\)の平面図形は以上です。