大阪府公立高校入試2019年(平成31年)度の数学C問題問3の解説

2019年(平成31年)度に大阪府で行われた公立高校入試の数学C問題の問3の解説です。
第3問は立体、空間図形内の線分、面積、体積を求める総合問題です。
この問題に限ったことではありませんがイメージしにくい立体があるので、ながめているだけでは先に進めません。

2019年(平成31年)度の大阪府公立高校入試数学C問題と問3の解説

問題は大阪府で公開してくれています。

⇒　2019年大阪府C問題

※
解説に入れた図に記号をたくさん使いました。
計算式の中で違う記号を示していたら、察して下さい。笑

3.空間図形の総合問題

　\(\,\large{3}\,\)　は立体（空間図形）です。
最後の体積問題などは手を動かさなければ時間を無駄にするだけで、先ずお手上げでしょう。

図\(\,1\,\)、図\(\,2\,\)に共通する条件を書き出します。

　\(\,\mathrm{CDEF}\,\)は長方形
　\(\,\mathrm{DC=4}\,\)
　\(\,\mathrm{DE=5}\,\)
　\(\,\mathrm{AB \,/\!/\,DE}\,\)
　\(\,\mathrm{AB=3}\,\)
　\(\,\mathrm{AD=BE=8}\,\)
　\(\,\mathrm{AC=AD}\,\)
　\(\,\mathrm{BF=BE}\,\)

条件が多いですが、並べるだけでは意味がありません。
図の中で確認しながら進めることです。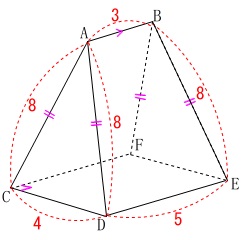三角柱ではありませんので注意が必要ですね。
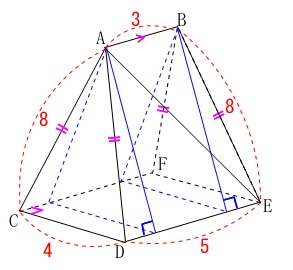四角錐2つと三角柱が組わっさってできています。

等脚台形の高さと面積

(1)
条件が加わります。

　\(\,\mathrm{GE=3}\,\)
　\(\,\mathrm{AE\, /\!/ \,GH}\,\)
　\(\,\mathrm{IH\,\perp\,AC}\,\)
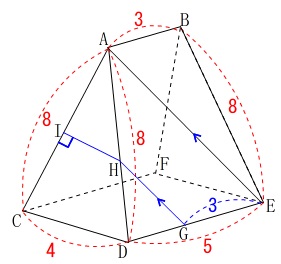①
\(\,\mathrm{△AEB}\,\)の面積を求めます。
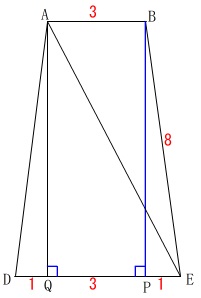台形\(\,\mathrm{ADEB}\,\)は等脚台形なので、
\(\,\mathrm{△ABE}\,\)の高さ\(\,\mathrm{BP}\,\)は三平方の定理から

　\(\begin{eqnarray}\displaystyle
\mathrm{BP}^2+\mathrm{PE}^2&=&\mathrm{BE}^2\\
\mathrm{BP}^2+1^2&=&8^2\\
\mathrm{BP}^2&=&64-1\\
&=&63\\
\mathrm{BP}&=&3\sqrt{7}　(\,\mathrm{BP}\,＞\,0\,)
\end{eqnarray}\)

よって

　\(\begin{eqnarray}\displaystyle
\mathrm{△ABE}&=&\frac{1}{2}\times \mathrm{AB}\times \mathrm{BP}\\
&=&\frac{1}{2}\times 3\times 3\sqrt{7}\\
&=&\underline{　\frac{9\sqrt{7}}{2}　(\mathrm{cm^2})}
\end{eqnarray}\)

平行線と相似と垂線の長さ

②
線分\(\,\mathrm{AH}\,\)の長さを求めます。
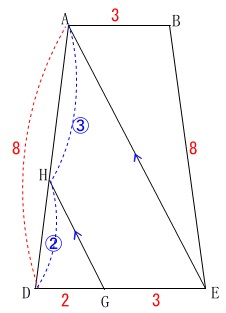相似利用ですね。

\(\,\mathrm{AE\, /\!/ \,HG}\,\)なので

　\(\,\mathrm{AH:HD=3:2}\,\)

よって

　\(\begin{eqnarray}\displaystyle
\mathrm{AH}&=&\frac{3}{5}\times \mathrm{AD}\\
&=&\frac{3}{5}\times 8\\
&=&\underline{　\frac{24}{5}　}　(\mathrm{cm})
\end{eqnarray}\)

③は\(\,\mathrm{IH}\,\)の長さです。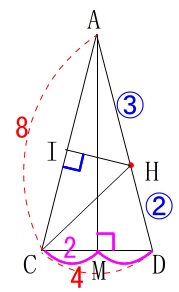
二等辺三角形\(\,\mathrm{ACD}\,\)の面積を利用しましょう。

\(\,\mathrm{A}\,\)から\(\,\mathrm{DC}\,\)に垂線を引くと線分\(\,\mathrm{DC}\,\)の中点\(\,\mathrm{M}\,\)に下りるので、

　\(\begin{eqnarray}\displaystyle
\mathrm{AM}^2+\mathrm{CM}^2&=&\mathrm{AC}^2\\
\mathrm{AM}^2+2^2&=&8^2\\
\mathrm{AM}^2&=&64-4\\
&=&60\\
\mathrm{AM}&=&2\sqrt{15}　(\,\mathrm{AM}\,＞\,0\,)
\end{eqnarray}\)

これから

　\(\begin{eqnarray}\displaystyle
\mathrm{△ACD}&=&\frac{1}{2}\times \mathrm{DC}\times \mathrm{AM}\\
&=&\frac{1}{2}\times 4\times 2\sqrt{15}\\
&=&\color{magenta}{4\sqrt{15}}
\end{eqnarray}\)
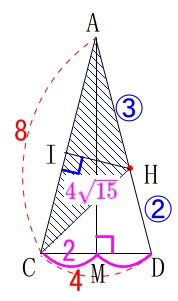ここで\(\,\mathrm{AH:HD=3:2}\,\)なので

　\(\begin{eqnarray}\displaystyle
\mathrm{\color{red}{△AHC}}&=&\frac{3}{5}\times \mathrm{△ACD}\\
&=&\frac{3}{5}\times 4\sqrt{15}\\
&=&\color{red}{\frac{12\sqrt{15}}{5}}
\end{eqnarray}\)

\(\,\mathrm{△AHC}\,\)は底辺\(\,\mathrm{AC}\,\)、高さ\(\,\mathrm{IH}\,\)と見ることもできるので、

　\(\begin{eqnarray}\displaystyle
\mathrm{\color{red}{△AHC}}&=&\frac{1}{2}\times \mathrm{AC}\times \mathrm{IH}\\
\color{red}{\frac{12\sqrt{15}}{5}}&=&\frac{1}{2}\times 8\times \mathrm{IH}\\
\mathrm{IH}&=&\frac{12\sqrt{15}}{5}\times \frac{1}{4}\\
&=&\underline{　\frac{3\sqrt{15}}{5}　}　(\mathrm{cm})
\end{eqnarray}\)

三角形を転がしても面積は変わらない、ということです。

(2)
条件が加わり、ちょっと形を見極めにくい立体になります。

加わる条件

　\(\mathrm{AJ=BK}=2\)
　\(\mathrm{JK}\, /\!/ \,\mathrm{CF}\)

この条件から分かることが

　\(\mathrm{JC=KF}\)　
これは横から見ても二等辺三角形ではありませんので注意が必要です。

相似の利用と面積と体積の求め方

①\(\,\mathrm{JK}\,\)の長さを求めます。

台形\(\,\mathrm{ADEB}\,\)を抜き出します。
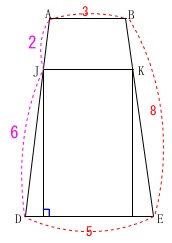\(\,\mathrm{AJ:JD=2:6=1:3}\,\)なので

　\(\begin{eqnarray}
\mathrm{JK}&=&\frac{3\times 3+1\times 5}{1+3}\\
&=&\frac{9+5}{4}\\
&=&\underline{　\frac{7}{2}　}
\end{eqnarray}\)

と済ませたいところですが、相似を使って説明しておきます。
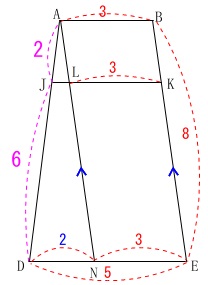\(\,\mathrm{BE}\,\)に平行になるように線分\(\,\mathrm{AN}\,\)を引きます。

四角形\(\,\mathrm{ANEB}\,\)は平行四辺形なので\(\,\mathrm{NE=\color{red}{3}}\,\)だから

　\(\begin{eqnarray}\displaystyle
\mathrm{\color{blue}{DN}}&=&\mathrm{DE-NE}\\
&=&\color{red}{5}-\color{red}{3}\\
&=&\color{blue}{2}
\end{eqnarray}\)

\(\,\mathrm{△AJL}\,\)　∽　\(\,\mathrm{△ADN}\,\)で相似比は\(\,\mathrm{1:4}\,\)だから

　\(\begin{eqnarray}\displaystyle
\mathrm{\color{magenta}{JL}}&=&\frac{1}{4}\times \mathrm{DN}\\
&=&\frac{1}{4}\times \color{blue}{2}\\
&=&\color{magenta}{\frac{1}{2}}
\end{eqnarray}\)

よって

　\(\begin{eqnarray}\displaystyle
\mathrm{JK}&=&\mathrm{\color{magenta}{JL}}+\mathrm{\color{red}{LK}}\\
&=&\color{magenta}{\frac{1}{2}}+\color{red}{3}\\
&=&\underline{　\frac{7}{2}　}
\end{eqnarray}\)

または、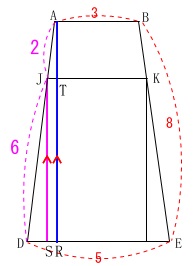\(\,\mathrm{AR}\,\)と\(\,\mathrm{JS}\,\)が平行となるように垂線\(\,2\,\)本を引いても左右対称なので求められます。

自分でやってみて下さい。
同じ結果が出なければどこかで計算ミスしています。笑

②
立体の体積です。

三角柱でも四角錐でもない立体の体積なので公式が使えません。
面積でも体積でも公式が使えないときは、
　『全体』－『部分』
または
　『部分』＋『部分』
を考えるようにすると良いですよ。

ここでは、
『四角錐』＋『三角柱』を利用します。

ただし、条件が変わっています。

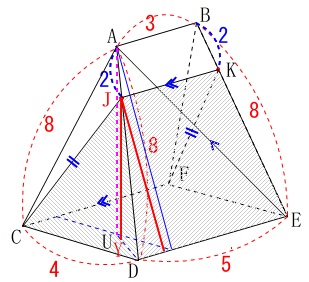
求めるのは立体\(\,\mathrm{JK-CDEF}\,\)の体積です。

立体\(\,\mathrm{AB-CDEF}\,\)と立体\(\,\mathrm{JK-CDEF}\,\)で共通しているのは四角錐の底面となる面積だけです。

立体\(\,\mathrm{JK-CDEF}\,\)の体積をいきなり求めるのは難しく感じるかもしれませんので、
立体\(\,\mathrm{AB-CDEF}\,\)の体積を求めるときはどうするかを考えて見ましょう。

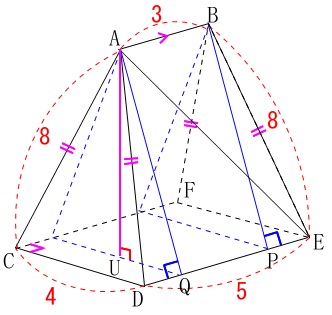\(\,\mathrm{A}\,\)から\(\,\mathrm{CDEF}\,\)に垂線を下ろします。

直角三角形\(\,\mathrm{AUQ}\,\)に三平方の定理を使って\(\,\mathrm{AU}\,\)を求めますが、
(1)の①で\(\,\mathrm{△AEB}\,\)の面積を求めるときに\(\,\mathrm{AQ}\,\)は\(\,\mathrm{BP}\,\)として求めているので

　\(\begin{eqnarray}
\mathrm{AU^2+UQ^2}&=&\mathrm{AQ^2}\\
\mathrm{AU}^2+2^2&=&(3\sqrt{7})^2\\
\mathrm{AU}^2&=&63-4\\
&=&59\\
\mathrm{AU}&=&\sqrt{59}
\end{eqnarray}\)

立体\(\,\mathrm{AB-CDEF}\,\)の体積は、

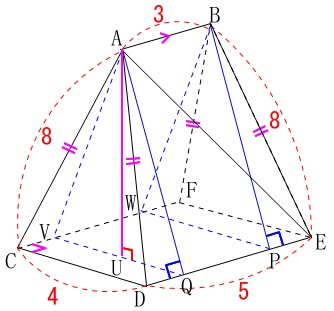
　\((\,四角錐\mathrm{A-CDQV}\,)\)
と
　\(\,(四角錐\mathrm{B-FEPW}\,)\)
は同じ体積なので

　\((\,四角錐\mathrm{A-CDQV}\,)\times 2\)＋\((\,三角柱\,\mathrm{AVQ-BWP}\,)\)

となります。

このまま立体\(\,\mathrm{AB-CDEF}\,\)の体積を求めても仕方ないので、
立体\(\,\mathrm{JK-CDEF}\,\)の体積に変えましょう。
垂線\(\,\mathrm{\color{red}{JY}}\,\)の長さが知りたいので\(\,\mathrm{△AUD}\,\)を抜き出して見ます。

図の縦横の比率は違いますが位置関係は
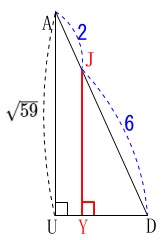となっているので、

　\(\begin{eqnarray}\displaystyle
\mathrm{\color{red}{JY}}&=&\frac{6}{8}\times \mathrm{AU}\\
&=&\frac{3}{4}\times \sqrt{59}\\
&=&\color{red}{\frac{3\sqrt{59}}{4}}
\end{eqnarray}\)

①から
　\(\displaystyle \mathrm{JK}=\color{magenta}{\frac{7}{2}}\,\)
対称性から\(\,\mathrm{DS=ZE}\,\)なので

　\(\begin{eqnarray}\displaystyle
\mathrm{DS}&=&\frac{\mathrm{DE-SZ}}{2}\\
&=&\frac{5-\frac{7}{2}}{2}\\
&=&\color{magenta}{\frac{3}{4}}
\end{eqnarray}\)

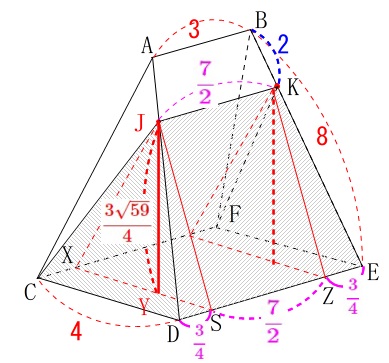求める体積は、

四角錐\(\,\mathrm{A-CDSX}\,\)の体積が

　\(\hspace{10pt}\displaystyle \frac{1}{3}\times \mathrm{DC}\times \mathrm{DS}\times \mathrm{JY}\\
\displaystyle =\frac{1}{3}\times 4\times \frac{3}{4}\times \frac{3\sqrt{59}}{4}\\
\displaystyle =\color{red}{\frac{3\sqrt{59}}{4}}\)

反対側の四角錐も同じ体積です。

間の三角柱は、

底面を
　\(\begin{eqnarray}
\mathrm{△JSX}&=&\frac{1}{2}\times \mathrm{SX}\times \mathrm{JY}\\
&=&\frac{1}{2}\times 4\times \frac{3\sqrt{59}}{4}\\
&=&\frac{3\sqrt{59}}{2}
\end{eqnarray}\)

高さを
　\(\displaystyle \mathrm{SZ}=\frac{7}{2}\,\)

と見ると体積は

　\(\displaystyle \frac{3\sqrt{59}}{2}\times \frac{7}{2}\\
\displaystyle =\color{red}{\frac{21\sqrt{59}}{4}}\)

よって求める体積\(\,V\,\)は

　\(\begin{eqnarray}
V&=&\color{red}{\frac{3\sqrt{59}}{4}}\times 2+\color{red}{\frac{21\sqrt{59}}{4}}\\
&=&\frac{6\sqrt{59}+21\sqrt{59}}{4}\\
&=&\underline{　\frac{27\sqrt{59}}{4}　}　(\mathrm{cm^2})
\end{eqnarray}\)

立体がイメージしにくい形なので、部分的に抜き出すことがポイントですね。

⇒　大阪府公立高校入試2019年(平成31年)度の数学C問題の過去問解説

\(\,\large{1}\,\)で確実に、素早く\(\,42\,\)点を確保しましょう。

⇒　大阪府公立高校入試2019年(平成31年)度の数学C問題第2問の解説

\(\,\large{2}\,\)の平面までの比較的計算が楽な問題で時間を余らせて、\(\,\large{3}\,\)で差をつける。

このレベルで受験をするなら、手を止めたらそこから先へは進めません。

⇒　全国の公立高校入試 数学過去問の解答解説

都道府県によっては得点しにくい問題はありますが、大阪府のC問題は公式を当てはめれば答えが出るという問題ではありません。