大阪府公立高校入試2019年(平成31年)度の数学C問題の過去問解説

2019年(平成31年)度に大阪府で行われた公立高校入試の数学C問題の過去問解説です。
C問題が出題される上位校受験者対象の解説になりますので、ある程度の基本はできている人向けの解説として省略するところがあります。
わかりにくい場合はB問題の解説も別のところでしておきますので基本の確認をしておいて下さい。

問題は大阪府で公開してくれています。

⇒　2019年大阪府C問題

問題は　\(\,\large{1}\,\)　\(\,\large{2}\,\)　\(\,\large{3}\,\)　と大問3つですが、割とボリュームのある問題ですよ。

ただ、方針がしっかりしている人にとっては前半はそれほど時間のかかる問題はありませんので、前半で時間を稼いでおく方が満点は狙いやすいでしょう。

1.小問集合

\(\,\large{1}\,\)　は小問集合で(1)から(8)まであります。

式の計算と数の大小比較問題

(1)
計算問題としても答えは簡単に出ます。
しかし、計算問題だと勘違いしていいる人は高校に入ってから数学で苦戦するでしょう。

この問題では代入して計算してもしれているので一般向けとして普通に代入しておきます。

　\(\hspace{10pt}x^2-10x+2\\
=(5-2\sqrt{3})^2-10(5-2\sqrt{3})+2\\
=37-20\sqrt{3}-50+20\sqrt{3}+2\\
=\underline{　-11　}\)

しかし、『覚え太郎』会員はこんな計算しませんよね？

いつも通り処理して下さい。

　\(\begin{eqnarray}
(x-5)^2&=&(-2\sqrt{3})^2\\
x^2-10x+25&=&12\\
x^2-10x&=&-13
\end{eqnarray}\)

よって

　\(\hspace{10pt}x^2-10x+2\\
=(-13)+1\\
=\underline{　-11　}\)

変わらないように思うでしょうがでいずれ大きな差となりますよ。

(2)
これは連立方程式です。

\(\,\mathrm{A=B=C}\,\)の連立方程式ではどの2つを組み合わせても良いです。

　
　\( \begin{cases}
\hspace{7pt} x-y+1=-2y　･･･①\\ \\
\hspace{7pt} 3x+7=-2y　･･･②
\end{cases}\)

\(\,x,y\,\)の項を左辺に、定数項を右辺に集めます。

　\( \begin{cases}
\hspace{7pt} x+y=-1　･･･①’\\ \\
\hspace{7pt} 3x+2y=-7　･･･②’
\end{cases}\)

\(\,①’\times 2-②’\,\)より

　\(\hspace{14pt}2x+2y=-2\\
\underline{-)\,3x+2y=-7　}\\
\hspace{4pt}-x\hspace{24pt}=\hspace{4pt}5\\
\hspace{40pt}x=-5\)

このとき　\(y=4\)

答え　\(\,\underline{　x=-5\,,\,y=4　}\,\)

こんなにていねいに説明する必要もありませんね。
ちょっと飛ばしましょう。

(3)
見え見えのまとまりがあります。

　\(\hspace{10pt}(a+2b)^2+a+2b-2\\
=(\color{red}{a+2b})^2+(\color{red}{a+2b})-2\\
=\underline{　(a+2b+2)(a+2b-1)　}\)

不安がある人は文字で置く方が確実です。

　\(\hspace{10pt}(a+2b)^2+a+2b-2\\
=(\color{red}{a+2b})^2+(\color{red}{a+2b})-2\\
=\mathrm{\color{red}{A}}^2+\mathrm{\color{red}{A}}-2\\
=(\mathrm{A}+2)(\mathrm{A}-1)\\
=\underline{　(a+2b+2)(a+2b-1)　}\)

(4)
数の大小比較はやること決まっています。

　\(\hspace{10pt}\displaystyle \color{red}{\frac{8}{\sqrt{2}}}\\
=4\sqrt{2}\\
=\color{red}{\sqrt{32}}\)
また
　\(\hspace{10pt}\color{blue}{5.5}\\
=\sqrt{5.5^2}\\
=\color{blue}{\sqrt{30.25}}\)

よって
　\(\,\color{blue}{\sqrt{30.25}}\,＜\,\sqrt{31}\,＜\,\color{red}{\sqrt{32}}\,\)
なので

　\(\,\color{blue}{5.5}\,＜\,\sqrt{31}＜\,\displaystyle \color{red}{\frac{8}{\sqrt{2}}}\,\)

答え　\(\,\underline{　オ　}\,\)

確率と標本調査

(5)
2つのさいころの出る目を\(\,a,b\,\)とするとき
　\(\displaystyle \frac{2b}{a}\)が素数
となる確率です。

樹形図で簡単に終わりますが、さいころ2つなので表でも良いです。

ここでは分子の\(\,2b\,\)だけを表に並べておきます。
\(\,a\,\)は\(\,1\,\)から\(\,6\,\)までの整数なので割って素数になる\(\,a\,\)だけを書き出します。

\(\begin{array}{|c|c|c|} \hline
　b　&　2b　&　\frac{2b}{a}\,が素数となる\,a\,　\\ \hline
　1　&　2　&　1　\\ \hline
　2　&　4　&　2　\\ \hline
　3　&　6　&　2\,,\,3　\\ \hline
　4　&　8　&　4　\\ \hline
　5　&　10　&　2\,,\,5　\\ \hline
　6　&　12　&　4\,,\,6　\\ \hline
\end{array}\)

よって

　\(\displaystyle \frac{9}{36}=\underline{　\frac{1}{4}　}\)

\(2≦2b≦12\)　なので\(\,a\,\)割って出てくる素数は　\(2,3,5,7,11\)　のどれかです。
分数になるものはすぐに除外できるので\(\,36\,\)通りさっと調べるだけですね。

\(\,1\,\)は素数ではありません。

(6)
標本調査は比例式で簡単に終わります。

碁石でも何でも良いので「黒」と「白」で良いです。

最初の袋の中は
　
　\(\,黒\,:\,白=32:8=\color{red}{4}:\color{red}{1}\,\)

全体に白を\(\,100\,\)加えると

　\(\,黒\,:\,白=28:12=\color{blue}{7}:\color{blue}{3}\,\)

最初の袋には黒と白が\(\,\color{red}{4}:\color{red}{1}\,\)で入っていたので、

黒が\(\,\color{red}{4x}\,\)個入っていたとすると
白は\(\,\color{red}{x}\,\)個入っていたことになります。

白を\(\,100\,\)加えると
黒が\(\,\color{blue}{4x}\,\)　白が\(\,\color{blue}{x+100}\,\)となっているので

　\(\begin{eqnarray}
\color{blue}{4x}:(\color{blue}{x+100})&=&\color{blue}{7}:\color{blue}{3}\\
3\times 4x&=&7\times (x+100)\\
12x&=&7x+700\\
x&=&140
\end{eqnarray}\)

この\(\,x\,\)は最初の白です。
最初の黒は、およそ

　\(4x=4\times 140\,=\,\underline{　560　}　個\)

文字式の利用と座標の設定問題

(7)
連続する2つの奇数を整数\(\,m\,\)を用いて
　
　\(a=2m-1\)
　\(b=2m+1\)

とおけば条件通りに進めるだけで答えは出ます。

条件を整理しておきます。

　\(0\,＜\,a\,＜\,100\)
　\(0\,＜\,b\,＜\,100\)

から

　\(0\,＜\,2m-1\,＜\,100\)
　\(0\,＜\,2m+1\,＜\,100\)

これを合わせると

　\(1\,≦\,m\,≦\,49\)

これはあとで使います。

　「\(\,b^2-a^2\,\)は\(\,100\,\)の倍数」

なので、

　\(\begin{eqnarray}
b^2-a^2&=&(2m+1)^2-(2m-1)^2\\
&=&8m
\end{eqnarray}\)

\(\,8m\,\)が\(\,100\,\)の倍数になるのは、

　\(\,m\,\)が\(\,25\,\)の倍数

のときだけなので\(1\,≦\,m\,≦\,49\)から

　\(\,m=25\,\)

のときだけで

　\(a=2\times 25-1\,=\,\underline{　49　}\)
　\(b=2\times 25+1\,=\,\underline{　51　}\)

文字式の基本ですね。

\(\,m\,\)が\(\,25\,\)の倍数となるのは\(\,k\,\)を整数として

　\(\begin{eqnarray}
8\,m&=&100\,k\\
2\,m&=&25\,k
\end{eqnarray}\)

\(\,2\,\)と\(\,25\,\)は公約数を\(\,1\,\)以外に持たないので（互いに素なので）
　\(\,m\,\)は\(\,25\,\)の倍数
　\(\,k\,\)は\(\,2\,\)の倍数
でなければ成り立たないからです。

分からなければ\(\,100\,\)の倍数になる\(\,m\,\)を調べれば済むことです。
\(\,m\,\)が\(\,5\,\)の倍数だろうと言うことは推測できるでしょう。
　
(8)
長い日本文ですが条件を抜き出してグラフに書き込みましょう。

　\(\,m\,:\,\displaystyle y=\frac{1}{8}x^2\,\)
　\(\,\ell\,:\,y=3x+2\,\)
　\(\,\mathrm{A}\,\)の座標は\(\,(\,t\,,\,3t+2\,)\,\)
　\(\,\mathrm{B}\,\)の座標は\(\,(\,t\,,\,0\,)\,\)
　\(\,\mathrm{DE=AB}\,\)
　\(\,\mathrm{EC=CF}\,\)

グラフで見ると、
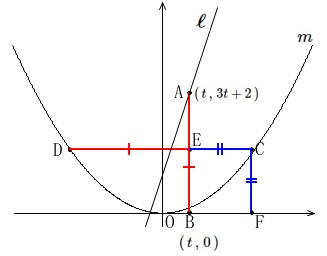分かることを書き出していきましょう。

　\(\,\mathrm{A}\,(\,\color{red}{t}\,,\,\color{blue}{3t+2}\,)\,\)
　\(\,\mathrm{B}\,(\,\color{red}{t}\,,\,0\,)\,\)

と同じく\(\,\mathrm{E}\,\)の\(\,x\,\)座標も\(\,\color{red}{t}\,\)です。

ここで\(\,\mathrm{AB=DE}\,\)なので、

\(\,\mathrm{D}\,\)の\(\,x\,\)座標は

　\(\hspace{10pt}\color{red}{t}-(\color{blue}{3t+2})\\
=-2t-2\)

\(\,\mathrm{D}\,\)が\(\,m\,\)上の点なので

　\(\displaystyle \mathrm{D}\,\left(\,-2t-2\,,\,\frac{1}{8}(-2t-2)^2\,\right)\,\)

\(\,\mathrm{C}\,\)の座標は\(\,\mathrm{D}\,\)と\(\,y\,\)軸対称なので

　\(\displaystyle \mathrm{C}\,\left(\,2t+2\,,\,\frac{1}{8}(2t+2)^2\,\right)\,\)

\(\,\mathrm{F}\,\)は\(\,\mathrm{C}\,\)と\(\,x\,\)座標が同じなので

　　\(\displaystyle \mathrm{F}\,\left(\,2t+2\,,\,0\,\right)\,\)
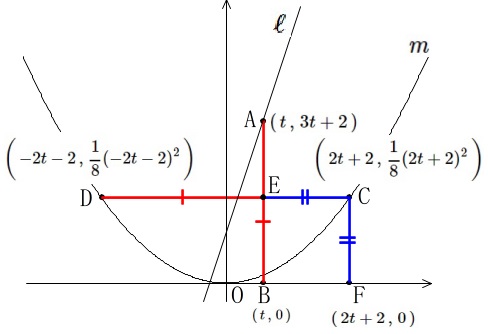ここで条件が\(\,\mathrm{EC=CF}\,\)なので

\(\,\mathrm{EC}\,\)が\(\,x\,\)座標の差、\(\,\mathrm{CF}\,\)が\(\,y\,\)座標の差であることから

　\(\begin{eqnarray}
\mathrm{EC}&=&\mathrm{CF}\\
(2t+2)-t&=&\frac{1}{8}(2t+2)^2
\end{eqnarray}\)

整理すると

　\(t^2=3\)

\(\,t\,＞\,0\,\)なので

　\(\,t=\underline{　\sqrt{3}　}\,\)

\(\,\large{1}\,\)の小問集合は以上です。

⇒　大阪府公立高校入試2019年(平成31年)度の数学C問題第2問の解説

\(\,\large{2}\,\)は平面図形の総合問題ですが割と楽な数値で処理できます。

⇒　大阪府公立高校入試2019年(平成31年)度の数学C問題問3の解説

\(\,\large{3}\,\)は空間図形（立体）の総合問題で勝負どころです。

応用問題が多めで長くなるので分けておきます。