2018年(平成30年度)奈良県公立高校入試の数学問題の解説【後半】

2018年(平成30年度)に奈良県で行われた公立高校入試の数学問題後半の解説です。
大問3は正方形の折り返した図形の性質を問われる問題です。
大問4は円周角の定理から面積比までの平面図形総合問題です。
問題文の長さが全く違いますが、どちらもただ見ているだけでは先に進みません。
手のつけようのない難問ではありませんので、応用問題への取り組み方を確認しておくと良いでしょう。

問題は奈良県でも公開してくれています。

⇒　2018年奈良県公立高校入試問題

3.三等分点と折り返しの相似な図形

問題文が長いのでとりつきにくいかもしれませんが、
分かり易い誘導となっていますので一つひとつ条件を整理すると割と簡単に答えにたどり着けます。

ただし、問題文をぼーとながめているだけでは処理できることが限られるのはいうまでもありません。

等間隔の平行線と等分点

「正方形の\(\,1\,\)辺を\(\,3\,\)等分する方法」を調べます。

(1)
ノートの罫線が等間隔で引かれていることを利用して\(\,3\,\)等分します。
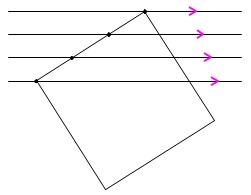正方形に限らず等間隔の平行線は線分を等分します。
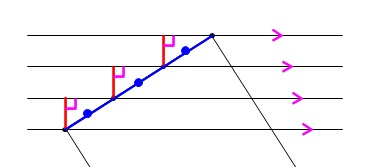平行線の性質から相似でもあり合同でもあるので、
各平行線によって正方形の\(\,1\,\)辺は\(\,3\,\)等分されることになりますね。

答え　\(\,\underline{　イ　}\,\)

折り返しの性質と三平方の定理

(2)
花子さんが調べた方法です。

　\(\color{black}{\fbox{1}}\)上下に半分に折る。

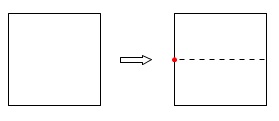
　\(\color{black}{\fbox{2}}\)折り目の左端に、右下の頂点が重なるように折り、
　右の辺と上の辺の交点に印をつける。

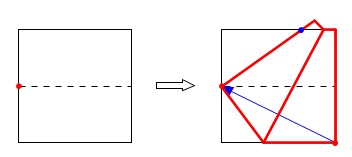
　\(\color{black}{\fbox{3}}\)\(\color{black}{\fbox{2}}\)でつけた印に左上の頂点が重なるように折る。

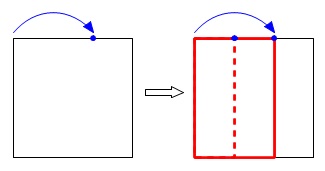
ここで上の辺についた折り目が\(\,3\,\)等分点になるという方法です。

では、何故\(\color{black}{\fbox{1}}\)\(\color{black}{\fbox{2}}\)\(\color{black}{\fbox{3}}\)のような折り方をすれば\(\,3\,\)等分点になるかを説明していきましょう。

①
\(\color{black}{\fbox{1}}\)\(\color{black}{\fbox{2}}\)\(\color{black}{\fbox{3}}\)でついた折り目に記号をつけます。
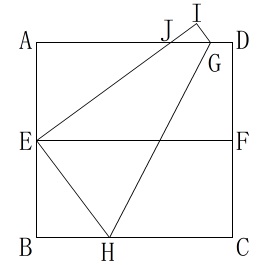\(\,\mathrm{J}\,\)が\(\,\mathrm{AD}\,\)の\(\,3\,\)等分点の1つになれば良い、ということの説明です。

\(\,\mathrm{AD}\,\)の長さを\(\,1\,\)とすると、
\(\,\mathrm{JD}\,\)の長さが\(\,\displaystyle \underline{　\frac{1}{3}　}\,\)になれば良い。

ということから、言い換えると
　\(\,\mathrm{JD}=x\,\)
とおいて立てた方程式の解が\(\,\displaystyle \underline{　\frac{1}{3}　}\,\)になれば良い。

折り返しでは、

　折り返した辺と折り返された辺は等しく
　折り返した角と折り返された角は等しい

また、

　\(\,\mathrm{GH}\,\)は折り返した図形の軸

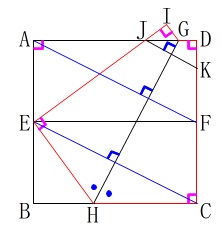
なので、

　\(\,\mathrm{EC}\,/\!/\,\mathrm{AF}\,/\!/\,\mathrm{JK}\,\)

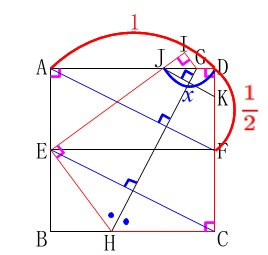
が言えて、

　\(\,\mathrm{△ADF}\,\)　∽　\(\,\mathrm{△JDK}\,\)

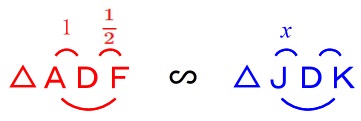
なので

\(\begin{eqnarray}
\mathrm{AD:JD}&=&\mathrm{DF:DK}\\
\color{red}{1}:\color{blue}{x}&=&\color{red}{\frac{1}{2}}:\mathrm{\color{blue}{DK}}\\
\mathrm{DK}&=&\underline{　\frac{1}{2}x　}
\end{eqnarray}\)

答え　
　\(\color{black}{\fbox{　あ　}}\)　\(\displaystyle \,\underline{　\frac{1}{3}　}\,\)　\(\color{black}{\fbox{　い　}}\)　\(\displaystyle \underline{　\frac{1}{2}x　}\)

②
\(\,\mathrm{DK}\,\)は\(\,\mathrm{GH}\,\)を軸として対称移動された線分\(\,\mathrm{IJ}\,\)と等しくなります。
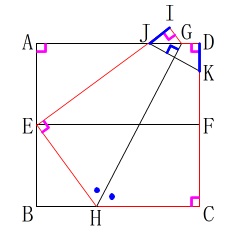　\(\displaystyle \mathrm{IJ=DK}=\color{red}{\frac{1}{2}x}\)

線分\(\,\mathrm{IE}\,\)に注目すると

　\(\,\mathrm{IE=IJ+JE}\,\)

なので\(\,\mathrm{IE}\,\)が正方形の\(\,1\,\)辺を折り返された線分であることから

　\(\begin{eqnarray}\displaystyle
\mathrm{JE}&=&\mathrm{IE-IJ}\\
&=&\color{blue}{1-\frac{1}{2}x}
\end{eqnarray}\)

さらに\(\,\mathrm{JD}=x\,\)とおいているので

　\(\begin{eqnarray}
\mathrm{AJ}&=&\mathrm{AD-JD}\\
&=&\color{magenta}{1-x}
\end{eqnarray}\)
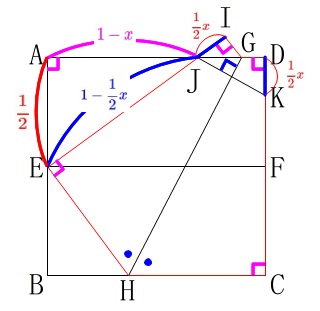　直角三角形\(\,\mathrm{△AEJ}\,\)に三平方の定理を用いると、

　\(\begin{eqnarray}
\mathrm{AE^2+AJ^2}&=&\mathrm{EJ^2}\\
\left(\frac{1}{2}\right)^2+(1-x)^2&=&\left(1-\frac{1}{2}x\right)^2
\end{eqnarray}\)

が成り立ちます。

答え　\(\displaystyle \,\underline{　\left(\frac{1}{2}\right)^2+(1-x)^2=\left(1-\frac{1}{2}x\right)^2　}\,\)

この方程式を解く必要はありません。

\(\,0\,＜\,x\,＜\,1\,\)から

　\(\displaystyle \,x=\frac{1}{3}\,\)

となることは分かっています。笑

4.円と相似と面積比

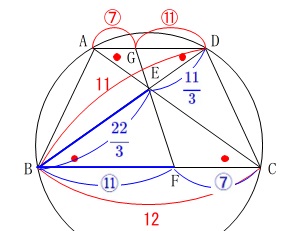
\(\color{black}{\fbox{　4　}}\)

条件をまとめておきます。

　円周上に\(\,4\,\)点\(\,\mathrm{A,B,C,D}\,\)がある。
　\(\,\mathrm{AD}\, /\!/ \,\mathrm{BC}\,\)
　\(\,\mathrm{BE=BF}\,\)
　\(\,\mathrm{AD=6}\,\)
　\(\,\mathrm{BC=12}\,\)
　\(\,\mathrm{AC=11}\,\)
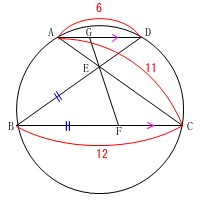これらの条件から分かることはたくさんあります。

最も分かり易いのは、円に平行線があるので、

　四角形\(\,\mathrm{ABCD}\,\)は等脚台形

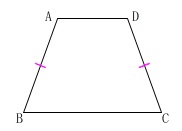
だということですね。

このことからいろいろなことが分かりますが、問題に合わせて進めた方がはやいでしょう。

円周上の4点と線分の作る相似

(1)
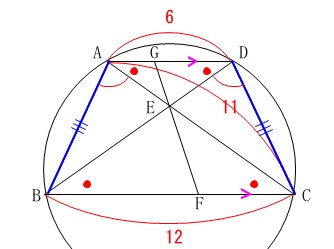
　\(\,\mathrm{△AEG}\,\)　∽　\(\,\mathrm{△CEF}\,\)

を証明します。

合同や相似の証明をするときは図の中で証明を済ませておきましょう。
後はそれを成立条件とともにまとめるだけです。
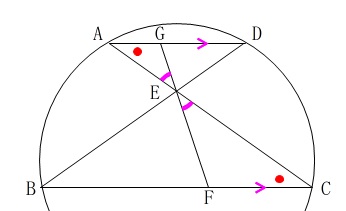円周角が等しいことや等脚台形なので等しい角や辺もたくさんありますが、
平行線の錯角と対頂角だけで十分です。

　　\(\,\mathrm{AD}\, /\!/ \,\mathrm{BC}\,\)

なので錯角が利用できます。

（証明）
　\(\,\mathrm{△AEG}\,\)と\(\,\mathrm{△CEF}\,\)において
\(\,\mathrm{AD}\, /\!/ \,\mathrm{BC}\,\)であることから、平行線の錯角は等しいから
　\(\mathrm{∠EAG=∠ECF}　･･･①\)
また、対頂角は等しいので
　\(\mathrm{∠AEG=∠CEF}　･･･②\)
①②より
　\(\,2\,\)組の角がそれぞれ等しい
ので、
　\(\,\mathrm{△AEG}\,\)　∽　\(\,\mathrm{△CEF}\,\)
（終わり）

(2)
\(\,\mathrm{∠ECF}=\color{red}{a^{\circ}}\,\)とすると
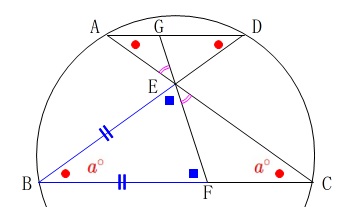\(\mathrm{∠EAG=∠ECF}=\color{red}{a^{\circ}}\,\)であり、
同一弧（\(\,\mathrm{\stackrel{\large{\frown}}{\mbox{DC}}}\,\)）の円周角は等しいので、

　\(\,\mathrm{∠CBD}=\color{red}{a^{\circ}}\,\)

ここで

　\(\,\mathrm{\color{blue}{BE}=\color{blue}{BF}}\,\)

なので\(\,\mathrm{△BEF}\,\)は二等辺三角形だから底角が等しく、

　\(\begin{eqnarray}\displaystyle
\mathrm{∠BEF}&=&\mathrm{\color{blue}{∠BFE}}\\
&=&\color{blue}{\frac{180-a}{2}^{\circ}}
\end{eqnarray}\)

三角形の内角の和でも良いですが、

　\(\,\mathrm{\color{blue}{∠BFE}=\color{red}{∠ECF}+∠CEF}\,\)

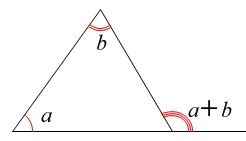
を利用しましょう。

　\(\begin{eqnarray}\displaystyle
\mathrm{\color{blue}{∠BFE}}&=&\mathrm{\color{red}{∠ECF}}+\mathrm{\color{magenta}{∠CEF}}\\
\color{blue}{\left(\frac{180-a}{2}\right)^{\circ}}&=&\mathrm{\color{magenta}{∠ECF}}+\color{red}{a^{\circ}}\\
\color{magenta}{\mathrm{∠ECF}}&=&\color{blue}{\left(\frac{180-a}{2}\right)^{\circ}}-\color{red}{a^{\circ}}\\
&=&\underline{　\left(\frac{180-3a}{2}\right)^{\circ}　}\\
または\\
&=&\underline{　90^{\circ}-\frac{3a}{2}^{\circ}　}
\end{eqnarray}\)

等脚台形の性質と線分の長さ

(3)
円に平行線を引くと等脚台形となります。
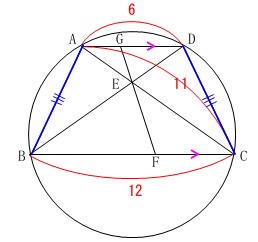平行線の錯角と円周角の定理から、
\(\,\mathrm{BC}\,\)を共通に持つ三角形\(\,\mathrm{ABC}\,\)と三角形\(\,\mathrm{DCB}\,\)が合同だからです。
等脚台形のときに限らず台形では垂線を利用することが多いので覚えておくと良いです。

\(\,\mathrm{A}\,\)と\(\,\mathrm{D}\,\)から\(\,\mathrm{BC}\,\)に垂線を引くと長方形ができます。

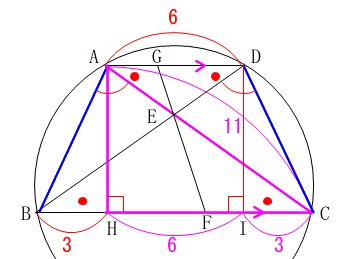
このとき\(\,\mathrm{BH=IH=3}\,\)になるので、
\(\,\mathrm{△ACH}\,\)に三平方の定理を用いて、

　\(\begin{eqnarray}
\mathrm{AC^2}&=&\mathrm{AH^2+CH^2}\\
11^2&=&\mathrm{AH^2}+9^2\\
\mathrm{AH^2}&=&11^2-9^2\\
&=&121-81\\
&=&40\\
\mathrm{AH}&=&\color{blue}{2\sqrt{10}}　(\,\mathrm{AH}\,＞\,0\,)
\end{eqnarray}\)
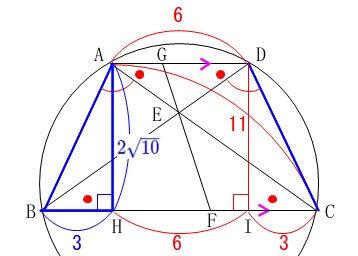今度は\(\,\mathrm{△ABH}\,\)に三平方の定理を用いて、

　\(\begin{eqnarray}
\mathrm{AB^2}&=&\mathrm{BH^2+AH^2}\\
&=&3^2+(2\sqrt{10})^2\\
&=&9+40\\
&=&49\\
\mathrm{AB}&=&\underline{　7　}　(\,\mathrm{AB}\,＞\,0\,)
\end{eqnarray}\)

説明は長いですけど、やっていることは三平方の定理を\(\,2\,\)度使っただけです。

相似を利用した面積比

(4)
\(\,\mathrm{△ABE}\,\)と\(\,\mathrm{△AEG}\,\)の面積を比較します。

\(\,\mathrm{△ABE}\,\)も\(\,\mathrm{△AEG}\,\)も\(\,\mathrm{△ABD}\,\)の中にあるので\(\,\mathrm{△ABD}\,\)を基準に考えると分かり易いです。

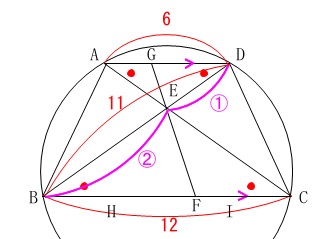
\(\,\mathrm{△ABC}\,\)　≡　\(\,\mathrm{△DCB}\,\)なので
　\(\,\mathrm{AC=DB}=\color{red}{11}\,\)

\(\,\mathrm{△AEG}\,\)　∽　\(\,\mathrm{△CEF}\,\)と同様に

　\(\,\mathrm{△GED}\,\)　∽　\(\,\mathrm{△FEB}\,\)

なので相似比\(\,1：2\,\)から

　\(\mathrm{ED:EB}=\color{magenta}{1}：\color{magenta}{2}\)

このことから

　\(\displaystyle \mathrm{ED}=\color{blue}{\frac{11}{3}}\)

　\(\displaystyle \mathrm{EB}=\color{blue}{\frac{22}{3}}\)

また\(\,\mathrm{BE=BF}\,\)なので

　\(\displaystyle \mathrm{BF}=\color{blue}{\frac{22}{3}}\,\)
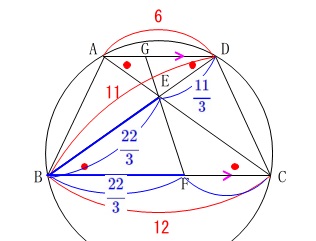\(\,\mathrm{BC}=\color{red}{12}\,\)

から

　\(\begin{eqnarray}\displaystyle
\mathrm{FC}&=&\mathrm{BC-BF}\\
&=&12-\frac{22}{3}\\
&=&\frac{36-22}{3}\\
&=&\color{magenta}{\frac{14}{3}}
\end{eqnarray}\)

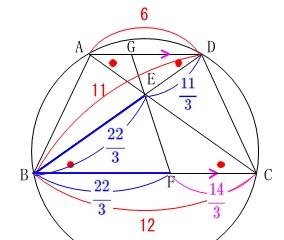よって

　\(\begin{eqnarray}
\mathrm{BF:FC}&=&22:14\\
&=&\color{blue}{11}:\color{blue}{7}
\end{eqnarray}\)
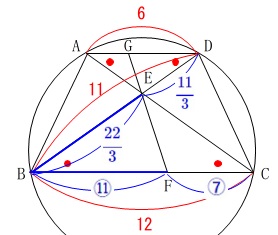相似な図形から\(\,\mathrm{DG:GA}\,\)の比も同じで

　\(\mathrm{GD:AG}=\color{red}{11}:\color{red}{7}\)
\(\,\mathrm{△ABD}\,\)を基準に面積を表すと

　\(\displaystyle \mathrm{△ABE}=\mathrm{△ABD}\times \color{blue}{\frac{2}{3}}\)

　\(\displaystyle \mathrm{△AEG}=\mathrm{△ABD} \times \color{blue}{\frac{1}{3}}\times \color{red}{\frac{7}{18}}\)

よって\(\,\mathrm{△ABE}\,\)の面積は\(\,\mathrm{△AEG}\,\)の

　\(\hspace{10pt}\displaystyle \color{blue}{\frac{2}{3}}\div \frac{\color{blue}{1}\times \color{red}{7}}{\color{blue}{3}\times \color{red}{18}}\\
\displaystyle =\color{blue}{\frac{2}{3}}\times \frac{\color{blue}{3}\times \color{red}{18}}{\color{blue}{1}\times \color{red}{7}}\\
\displaystyle =\underline{　\frac{36}{7}　}　(倍)\)

相似や合同を見つけて、それぞれの比を自分で図に書き込んで行けば見た目よりは簡単です。

底辺も高さも分かっているので具体的に面積を求めても良いです。
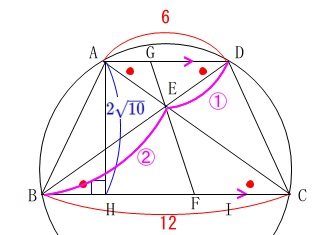底辺を\(\,\mathrm{AD}\,\)、高さを\(\,\mathrm{AH}\,\)と見ると

　\(\begin{eqnarray}\displaystyle
\mathrm{△ABD}&=&\frac{1}{2}\times \mathrm{AD}\times \mathrm{AH}\\
&=&\frac{1}{2}\times 6\times 2\sqrt{10}\\
&=&6\sqrt{10}
\end{eqnarray}\)

なので

　\(\begin{eqnarray}\displaystyle
\mathrm{△ABE}&=&\frac{2}{3}\times 6\sqrt{10}\\
&=&4\sqrt{10}
\end{eqnarray}\)

　\(\begin{eqnarray}\displaystyle
\mathrm{△AEG}&=&\frac{1}{3}\times \frac{7}{18}\times 6\sqrt{10}\\
&=&\frac{7\sqrt{10}}{9}
\end{eqnarray}\)

よって、

　\(\begin{eqnarray}\displaystyle
\mathrm{△ABE}&=&4\sqrt{10}\div \frac{7\sqrt{10}}{9}\times \mathrm{△AEG}\\
&=&4\sqrt{10}\times \frac{9}{7\sqrt{10}}\times \mathrm{△AEG}\\
&=&\underline{　\frac{36}{7}　}\times \mathrm{△AEG}
\end{eqnarray}\)

\(\,2018\,\)年度の奈良県の公立入試問題の解説は以上です。

⇒　2018年(平成30年度)奈良県公立高校入試の数学問題の解説

\(\color{black}{\fbox{　1　}}\)から通して見ておくと良いですよ。
全体の問題構成と傾向は毎年それほど変わるものではありません。

⇒　全国の公立高校入試 数学過去問の解答解説

\(\,2019\,\)年度の問題も解説しますので参考にしてください。

⇒　奈良県公立高校入試問題2019年(平成31年)度の数学の過去問解説

\(\,2019\,\)年も問題構成、応用範囲も同じ程度です。