2018年(平成30年度)に奈良県で行われた公立高校入試の数学問題の解説です。
大問数は4題ですが大問ごとに小問に分かれていますので、問題数が少ないわけではありません。
50点満点の試験ですが配点に気をつけて、目標点数に合わせて時間配分を考えておくと良いです。
問題は奈良県でも公開してくれています。
1.小問集合
\(\color{black}{\fbox{ 1 }}\)は\(\,(1)\,\)から\(\,(9)\,\)まであり、さらに小問に分かれ\(\,12\,\)問あります。
基本問題ばかりですが配点は全体の\(\,40\,\)％ありますので確実にとっておきましょう。
式の計算と2次方程式と割り算（除法）の原理
(1)
①
\(\hspace{10pt}3-(-5)\\
=3+5\\
=\underline{ 8 }\)
簡単な計算も、少しややこしくなった計算も（かっこ）を外す\(\,1\,\)行を書くだけで計算ミスは減りますよ。
②
\(\hspace{10pt}4\times (-3)^2\\
=4\times 9\\
=\underline{ 36 }\)
（かっこ）部分の処理からです。
③
\(\hspace{10pt}\displaystyle 12a^2b^2\div(-6ab)\div\frac{1}{2}ab\\
\displaystyle =-\frac{12a^2b^2}{1}\times \frac{1}{6ab}\times \frac{2}{ab}\\
=\underline{ -4 }\)
全体の符号が「－」になるので「－」を前に置き、
割り算は逆数のかけ算にすれば簡単に約分が進みます。
\(\hspace{10pt}\displaystyle 12a^2b^2\div(-6ab)\div\frac{1}{2}ab\\
\displaystyle =-\frac{12a^2b^2\times 2}{ 6ab\times ab}\\
=\underline{ -4 }\)
分数線を1つにすると少し楽になります。
\(\displaystyle \frac{1}{2}\color{red}{ab}\,\)の\(\,\color{red}{ab}\,\)は分子にあります。
逆数にするとき分母にまわるので注意しましょう。
④
\(\hspace{10pt}(x+4)(x+5)-(x+3)(x-3)\\
=(x^2+9x+20)-(x^2-9)\\
=x^2+9x+20-x^2+9\\
=\underline{ 9x+29 }\)
(2)
「\(\,2\,\)次方程式の解を求める」ことと、「\(\,2\,\)次方程式を解く」ことは同じことですよ。
\(\,2\,\)次方程式を解くときは因数分解を試すことが先ですが、できそうもないので解の公式です。
\(\begin{eqnarray}\displaystyle
2x^2+5x+1&=&0\\
x&=&\frac{-5\pm\sqrt{5^2-4\times 2\times 1}}{2\times 2}\\
&=&\frac{-5\pm\sqrt{25-8}}{4}\\
&=&\underline{ \frac{-5\pm\sqrt{17}}{4} }
\end{eqnarray}\)
(3)
割り算の原理そのものです。
「\(\,a\,\)を\(\,3\,\)で割ると商が\(\,b\,\)で余りが\(\,2\,\)」
\(\underline{ a=3b+2 }\)
答え \(\,\underline{ ア }\,\)
円周角の定理と凹四角形の内角
中心角と円周角の関係と、二等辺三角形の底角が等しいことを利用します。
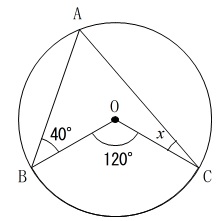中心角が\(\,120°\,\)なので円周角となる\(\,\mathrm{∠BAC=60^{\circ}}\,\)です。
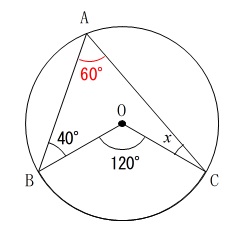
さらに、半径は常に等しいので
\(\,\mathrm{△OAB}\,\) と \(\,\mathrm{△OAC}\,\) は二等辺三角形で、
底角が等しくなるので、
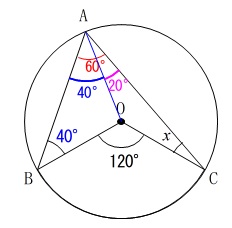
\(\,\mathrm{\color{blue}{∠OAB}=\color{blue}{∠OBA}}=\color{blue}{40^{\circ}}\,\)
\(\begin{eqnarray}
\mathrm{\color{magenta}{∠OAC}}&=&\mathrm{\color{red}{∠BAC}-\color{blue}{∠OAB}}\\
&=&\,\color{red}{60^{\circ}}-\color{blue}{40^{\circ}}\\
&=&\color{magenta}{20^{\circ}}
\end{eqnarray}\)
よって
\(x=\underline{ 20^{\circ} }\,\)
また、凹四角形\(\,\mathrm{ABOC}\,\)のおいて、
\(\mathrm{∠BOC}=\mathrm{∠ABO+∠BAC+∠ACO}\)
なので
\(\begin{eqnarray}
120^{\circ}&=&40^{\circ}+60^{\circ}+x\\
x&=&\underline{ 20^{\circ} }
\end{eqnarray}\)
でも良いですよ。
無理数の大小と自然数および素因数分解
(5)
数の大小比較は数字の世界をそろと分かり易いです。
⇒ ルートのついた無理数の不等式中の整数を表す文字の値を求める方法
\(5\,＜\,\sqrt{a}\,＜\,6\)
ここで
\(\,5=\sqrt{25}\,,\,6=\sqrt{36}\,\)
なので
\(\sqrt{25}\,＜\,\sqrt{a}\,＜\,\sqrt{36}\)
これを満たす自然数\(\,a\,\)は
\(\,26\,\)から\(\,35\,\)までの自然数で
\(35-26+1=\underline{ 10 } (個)\)
引き算するだけで\(\,9\,\)個と間違えないようにしましょう。
引き算は間隔の数なので\(\,+1\,\)が必要です。
または不等式全体が正の数の範囲なので、全体を\(\,2\,\)乗して
\(25\,＜\,a\,＜\,36\)
から数えても良いです。
(6)
4つの数の積が\(\,560\,\)です。
先ずは\(\,560\,\)を素因数分解しておきましょう。
\(2\underline{)\,560}\\
2\underline{)\,280}\\
2\underline{)\,140}\\
2\underline{)\hspace{6pt}70}\\
5\underline{)\hspace{6pt}35}\\
\hspace{20pt}7\)
\(560=2^4\times 5\times 7\)
このことから\(\,560\,\)を4つの数に分けるとすると
\(\,1\times 2^4\times 5\times 7\,\)
\(\,2\times 2^3\times 5\times 7\,\)
\(\,2^2\times 2^2\times 5\times 7\,\)
この中で\(\,1\,\)から\(\,9\,\)までの異なる4つの自然数の積になっているのは、
\(\,2\times 2^3\times 5\times 7\,\)
の
\(\underline{ 2\,,\,5\,,\,7\,,\,8 }\)
さいころ2つを同時に投げる確率
2つのさいころを同時に投げても、1つずつ投げても同じことです。
樹形図で良いですがさいころ2つの場合は表がはやいです。
少なくとも1つは\(\,5\,\)以上の目が出る場合は下の表の\(\,○\,\)がついた出方なので
\(\begin{array}{|c|c|c|c|c|c|c|} \hline
& \color{red}{1} & \color{red}{2} & \color{red}{3} & \color{red}{4} & \color{red}{5} & \color{red}{6}\\ \hline
\color{blue}{1} & & & & & ○ & ○\\ \hline
\color{blue}{2} & & & & & ○ & ○\\ \hline
\color{blue}{3} & & & & & ○ & ○\\ \hline
\color{blue}{4} & & & & & ○ & ○\\ \hline
\color{blue}{5} & ○ & ○ & ○ & ○ & ○ & ○\\ \hline
\color{blue}{6} & ○ & ○ & ○ & ○ & ○ & ○\\ \hline
\end{array}\)
\(\displaystyle \frac{20}{36}=\frac{5}{9}\)
答え \(\displaystyle \underline{ \frac{5}{9} }\)
「少なくとも\(\,1\,\)個は\(\,5\,\)以上」の反対（余事象）は,
「1つも\(\,5\,\)以上の目が出ない」
ということなので、全体から両方\(\,4\,\)以下の目の出方を引いて、
\(\displaystyle 1-\frac{16}{36}=\frac{36-16}{36}\)
としても良いです。
立方体の展開図と組み立てたときの重なる点
立方体を含めて、直方体の展開図を組み立てて、
立体の対角線上にある頂点は
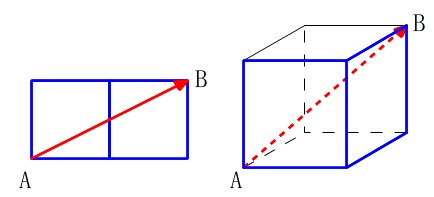断面2つ（二マス）の対角線上になります。
ここで、\(\color{black}{\fbox{な}}\)の左上と\(\color{black}{\fbox{ら}}\)の右下に注目すると、
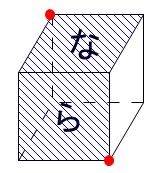アからエまでで二マスの対角線上にあるのは、
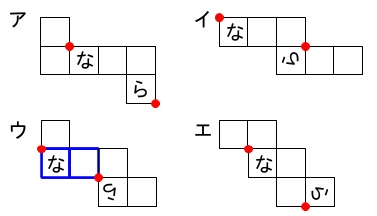
答え \(\,\underline{ ウ }\,\)
45度の作図
平行線\(\,\ell\,\)上の点\(\,\mathrm{P}\,\)の記入は最後です。
先ずは\(\,m\,\)上で\(\,\mathrm{∠PAB=45^{\circ}}\,\)を作図することを考えましょう。
\(\,45°\,\)は\(\,90°\,\)の半分
なので、
垂線の角の二等分線を引く
作図をすれば良いのです。
答え
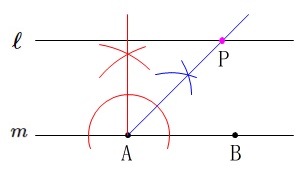点\(\,\mathrm{P}\,\)を書き込むのを忘れないようにしましょう。
2.2次関数と図形の融合
\(\color{black}{\fbox{ 2 }}\)は関数と図形の融合問題です。
問題全体に通じる条件を書き出しておきます。
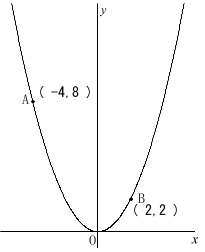
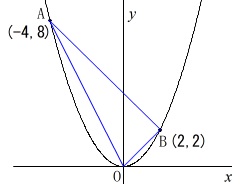
放物線の関数は\(\,\displaystyle \frac{1}{2}x^2\)
\(\,2\,\)点\(\,\mathrm{A,B}\,\)は放物線上の点
\(\,\mathrm{A\,(\,-4\,,\,8\,)}\,\)
\(\,\mathrm{B\,(\,2\,,\,2\,)}\,\)
yの変域（値域）の見方
(1)
\(\,x\,\)の変域が\(\,-4\,≦\,x\,≦\,2\,\)における\(\,y\,\)の変域を求めます。
\(\,y\,\)の変域は\(\,x\,\)の変域の範囲で、
\(\,y\,\)の最小値と最大値ではさむ範囲のことです。
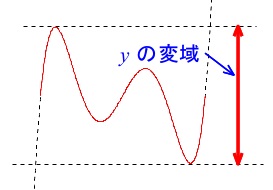両端が最大最小になるとは限りませんので注意して下さい。
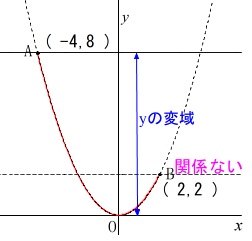
答え \(\,\underline{ 0\,≦\,y\,≦\,8 }\,\)
線分と交わる曲線
(2)
5つの関数が線分\(\,\mathrm{AB}\,\)と交わるものを選びます。
直線や半直線ではなく、線分なので限りがあります。
グラフを書けばすぐに終わります。
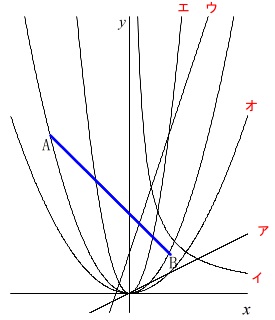線分\(\,\mathrm{AB}\,\)と交点を持つのは2つです。
答え \(\,\underline{ ウ , エ }\,\)
平行四辺形の面積を二等分する直線
(3)
条件が加わります。
\(\,\mathrm{A}\,\)を通り\(\,x\,\)軸と平行な直線と\(\,y\,\)軸との交点を\(\,\mathrm{C}\,\)
\(\,\mathrm{B}\,\)を通り\(\,x\,\)軸と平行な直線と放物線との交点を\(\,\mathrm{D}\,\)
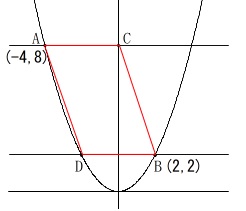
このとき四角形\(\,\mathrm{ADBC}\,\)の面積を\(\,2\,\)等分する直線の式を求めます。
四角形\(\,\mathrm{ADBC}\,\)は平行四辺形なので、
対角線の交点を通る直線が面積を\(\,2\,\)等分します。
対角線の交点は
\(\,\mathrm{A,B}\,\)の中点
または
\(\,\mathrm{C,D}\,\)の中点
になります。
対角線の交点を\(\,\mathrm{E}\,\)とすると\(\,\mathrm{E}\,\)の座標は
\(\displaystyle \left(\,\frac{-4+2}{2}\,,\,\frac{8+2}{2}\,\right)\\
\displaystyle =\color{magenta}{(\,-1\,,\,5\,)}\)
後は、原点\(\,\mathrm{O}\,\)と点\(\,\mathrm{E}\,\)を通る直線を求めれば良いだけです。
答え \(\displaystyle \underline{ y=-5x }\)
回転体の体積
(4)
\(\,\mathrm{△AOB}\,\)を\(\,x\,\)軸を軸として回転させた体積を求めます。
公式の使えない面積や体積を求めるときは、
『部分』＋『部分』
または
『全体』－『部分』
です。
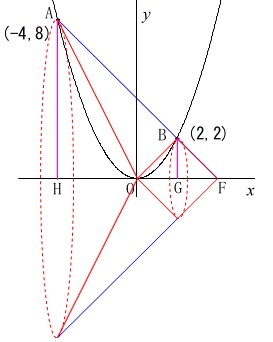
頂点を\(\,\mathrm{F}\,\)として底面の半径を\(\,\mathrm{AH}\,\)とする円錐の体積
から
頂点を\(\,\mathrm{F}\,\)、底辺の半径を\(\,\mathrm{BG}\,\)とする円錐の体積
と
頂点を\(\,\mathrm{O}\,\)、底辺の半径を\(\,\mathrm{BG}\,\)とする円錐の体積
を引けば求める\(\,\mathrm{△AOB}\,\)の回転体の体積です。
直線\(\,\mathrm{AB}\,\)の傾きは\(\,-1\,\)なので、
\(\,\mathrm{F}\,\)の\(\,x\,\)座標が\(\,4\,\)となることから
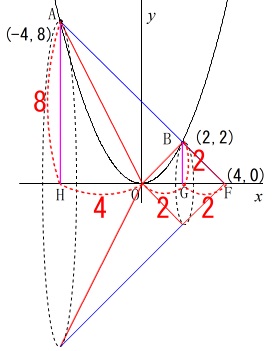それぞれの円錐の高さと底面の半径が分かるので、
\(\,\mathrm{F}\,\)を頂点、底面の半径を\(\,\mathrm{AH}\,\)とする円錐の体積は
\(\hspace{10pt}\displaystyle \frac{1}{3}\times \pi \times 8^2\times (4+2+2)\\
\displaystyle =\frac{512\,\pi}{3}\)
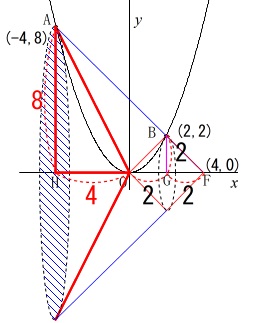
これが『全体』になります。
これから部分部分の円錐を引いていきます。
\(\,\mathrm{O}\,\)を頂点、底面の半径を\(\,\mathrm{AH}\,\)とする円錐の体積は
\(\hspace{10pt}\displaystyle \frac{1}{3}\times \pi \times 8^2\times 4\\
\displaystyle =\frac{256\,\pi}{3}\)
\(\,\mathrm{F}\,\)を頂点、底面の半径を\(\,\mathrm{BG}\,\)とする円錐の体積は
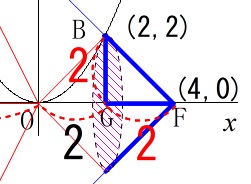
\(\hspace{10pt}\displaystyle \frac{1}{3}\times \pi \times 2^2\times 2\\
\displaystyle =\frac{8\,\pi}{3}\)
\(\,\mathrm{O}\,\)を頂点、底面の半径を\(\,\mathrm{BG}\,\)とする円錐の体積は
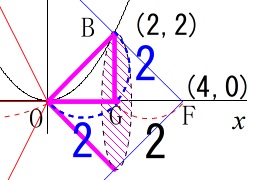
\(\hspace{10pt}\displaystyle \frac{1}{3}\times \pi \times 2^2\times 2\\
\displaystyle =\frac{8\,\pi}{3}\)
よって、求める\(\,\mathrm{△AOB}\,\)の回転体の体積\(\,\mathrm{V}\,\)は
\(\begin{eqnarray}\displaystyle
\mathrm{V}&=&\frac{512\,\pi}{3}-\frac{256\,\pi}{3}-2\times \frac{8\,\pi}{3}\\
&=&\frac{(512-256-16)\pi}{3}\\
&=&\frac{240\,\pi}{3}\\
&=&\underline{ 80\,\pi }
\end{eqnarray}\)
ここでは部分的に円錐の計算をしていますが、\(\displaystyle \frac{1}{3}\,\pi\,\)は共通しているので、
まとめて計算するともう少し楽になりますね。
全問通してとも考えましたが、少し長くなりますので分けます。
⇒ 2018年(平成30年度)奈良県公立高校入試の数学問題の解説【後半】
\(\color{black}{\fbox{ 3 }}\)は正方形の折り返し問題です。
\(\color{black}{\fbox{ 4 }}\)は円と円周角の定理に関する平面図形の総合問題です。
2019年度の問題も解説しますので参考にしてください。
クラブ活動で忙しい！
塾に通っているのに数学が苦手！
数学の勉強時間を減らしたい！
数学の勉強方法が分からない！
その悩み、『覚え太郎』が解決します！！！
