奈良県公立高校入試問題2019年(平成31年)度の数学の過去問解説

2019年(平成31年)度に奈良県で行われた公立高校入試問題の数学の過去問解説です。
大問は1から4まであります。
1は小問集合ですが配点が4割ありますので素早く確実に得点し、後に続く応用問題に進みましょう。
2018年同様に空間図形がないので割と取り組みやすいでしょうけど応用問題への取り組み方は変わりません。

奈良県公立高校入試問題2019年(平成31年)度の数学の問題

問題は奈良県も公開してくれています。

⇒　2019年奈良県公立高校入試の数学問題

奈良県公立高校入試問題2019年(平成31年)度の数学の解説

さらっと全体が確認できる程度は解説を入れておきます。
問題傾向が変わっているいうことはありませんので、
対策にして下さい。

第１問

　\(\color{black}{\fbox{　1　}}\)

(1)
計算問題です。
　
①
　\(\hspace{10pt}-5-7\\
=\underline{　-12　}\)
引くということは数直線上で左に移動するということです。

②
　\(\hspace{10pt}2\times (-5^2)\\
=2\times (-25)\\
=\underline{　-50　}\)

（かっこ）の中の処理が先です。

　\((-5)^2=25\)
と
　\((-5^2)=-25\)
は符号が違いますので注意しておきましょう。

③
　\(\hspace{10pt}(-3a)^2\times 2b\div 6ab\\
=\displaystyle \frac{(-3a)^2\times 2b}{6ab}\\
=\displaystyle \frac{9a^2\times 2b}{6ab}\\
=\underline{　3a　}\)

割り算は逆数のかけ算として約分処理するとはやいですよ。

④
　\(\hspace{10pt}(x+2)^2-(x+2)(x-2)\\
=(x^2+4x+4)-(x^2-4)\\
=x^2+4x+4-x^2+4\\
=\underline{　4x+8　}\)

(2)
連立方程式を解きます。

連立方程式を解くときの基本は\(\,1\,\)文字消去です。

　\(\begin{cases}
\hspace{7pt} 2x-5y=-2　･･･①\\ \\
\hspace{7pt} y=x-5　･･･②
\end{cases}\)

移項して加減法でも良いですが、代入法の方がはやいです。

②を①の\(\,y\,\)に代入します。

　\(\begin{eqnarray}
2x-5(x-5)&=&-2\\
2x-5x+25&=&-2\\
-3x&=&-2-25\\
&=&-27\\
x&=&9
\end{eqnarray}\)

これを②に代入して、

　\(\begin{eqnarray}
y&=&x-5\\
&=&9-5\\
&=&4
\end{eqnarray}\)

答え　\(\,\underline{　x=-\,,\,y=4　}\,\)

(3)
2次方程式

　\(x^2-7x-18=0\)

を解きます。

⇒　2次方程式の因数分解を利用する解き方のコツと注意点

因数分解から試します。

定数項が\(\,\color{red}{-18}\,\)なので
　\(\color{black}{\fbox{1×18}}\)　\(\color{black}{\fbox{2×9}}\)　\(\color{black}{\fbox{3×6}}\)
のどちらかの因数にマイナスがつく形です。

2つの因数を足して\(\,x\,\)の\(\,1\,\)次の項の係数\(\,\color{blue}{-7}\,\)になる組み合わせは
　\(\color{red}{\fbox{　+2　と　－9　}}\)
なので

　\(\begin{eqnarray}
x^2-7x-18&=&0\\
(x+2)(x-9)&=&0\\
x&=&\underline{　-2\,,\,9　}
\end{eqnarray}\)

因数分解できない場合は解の公式です。

⇒　2018年(平成30年度)奈良県公立高校入試の数学問題の解説

小問集合では解の公式タイプが多いので、解の公式は使えるようにしておきましょう。

(4)
数の大小比較です。

数の大小比較のポイントは数の世界の統一です。

⇒　ルートのついた平方根(無理数)と有理数の大小比較問題の解き方とコツ

表し方をそろえてみましょう。

小数にしても良いですがルートのついた数にそろえます。

　\(\color{red}{3.3}=\sqrt{3.3^2}=\color{red}{\sqrt{10.89}}\)

　\(\displaystyle \color{blue}{\frac{10}{3}}=\sqrt{\left(\frac{10}{3}\right)^2}=\color{blue}{\sqrt{\frac{100}{9}}}\)

　\(\color{magenta}{\sqrt{11}}\)

これですべてにルートはつきましたが、まだそろっていません。

ルートの中の数の分母を\(\,9\,\)にそろえます。

　\(\displaystyle \color{red}{3.3}=\sqrt{\frac{10.89\times 9}{9}}=\color{red}{\sqrt{\frac{98.01}{9}}}\)

　\(\displaystyle \color{blue}{\frac{10}{3}}=\color{blue}{\sqrt{\frac{100}{9}}}\)

　\(\displaystyle \color{magenta}{\sqrt{11}}=\color{magenta}{\sqrt{\frac{99}{9}}}\)

分子を比較すると最も大きい数は

　\(\displaystyle \underline{　\frac{10}{3}　}\)

答えは問題に与えられた数で答えます。

小数にそろえても良いですが、、、

　\(\displaystyle \color{blue}{\frac{10}{3}}=\color{blue}{3.333\cdots}\)

は分かり易いですが問題は\(\,\sqrt{11}\,\)です。

　\(3.1^2=9.3\)
　\(3.2^2=10.24\)
　\(3.3^2=10.89\)
　\(3.4^2=11.56\)

なので

　\(3.3\,＜\,\sqrt{11}\,＜\,3.4\)

ということまでは分かりますが、\(\displaystyle \frac{10}{3}\,\)との大小比較ができていません。

　\(3.31^2=10.9561\)
　\(3.32^2=11.0224\)

なので

　\(3.31\,＜\,\sqrt{11}\,＜\,3.32\)

よって

　\(\displaystyle 3.3\,＜\,\sqrt{11}\,＜\,\frac{10}{3}\)

正確に表現できるのはルートのついた数なので、数の世界をそろえる方向を考えるときの参考にして下さい。

(5)
円柱の表面積を求めます。

⇒　表面積や体積の求め方(三角柱,四角柱,円柱,球や半球)

展開図を書きます。

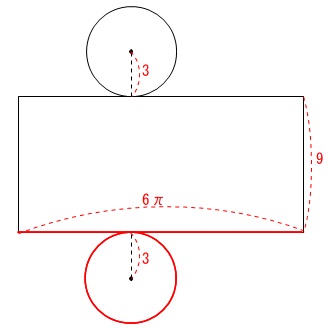
側面は長方形で横の長さは底面の円周と同じ、底面は円2つなので求める表面積は、

　\(\hspace{10pt}9\times 6\pi+2\times \pi(3^2)\\
=54\pi+18\pi\\
=\underline{　72\pi　}　(\,\mathrm{cm^2}\,)\)

(6)
単なる円周角の問題です。
　\(\mathrm{∠BAC}=116^{\circ}\)
なので中心角は（\(\,x\,\)の反対側です。）
　\(\mathrm{∠BOC}=232^{\circ}\)
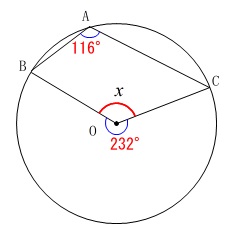よって、

　\(\begin{eqnarray}
x&=&360^{\circ}-232^{\circ}\\
&=&\underline{　128^{\circ}　}
\end{eqnarray}\)

\(\,\mathrm{∠BAC}\,\)の中心角が\(\,x\,\)ではないことには注意しましょう。

(7)
男子\(\,4\,\)人と女子\(\,2\,\)の中から2人を選ぶ確率です。

男子\(\,\color{red}{4}\,\)人と女子\(\,\color{blue}{2}\,\)人をそれぞれ区別します。
\(\,\color{red}{1,2,3,4}\,\)を男子、\(\,\color{blue}{5,6}\,\)を女子とすると
\(\,2\,\)人の選び方は

　\(\begin{array}{|c|c|c|} \hline
\color{red}{1} & \color{red}{2} &　\color{red}{ア}　\\ \hline
\color{red}{1} & \color{red}{3} &　\color{red}{ア}　\\ \hline
\color{red}{1} & \color{red}{4} &　\color{red}{ア}　\\ \hline
\color{red}{1} & \color{blue}{5} &　\color{blue}{イ}　\\ \hline
\color{red}{1} & \color{blue}{6} &　\color{blue}{イ}　\\ \hline
\color{red}{2} & \color{red}{3} &　\color{red}{ア}　\\ \hline
\color{red}{2} & \color{red}{4} &　\color{red}{ア}　\\ \hline
\color{red}{2} & \color{blue}{5} &　\color{blue}{イ}　\\ \hline
\color{red}{2} & \color{blue}{6} &　\color{blue}{イ}　\\ \hline
\color{red}{3} & \color{red}{4} &　\color{red}{ア}　\\ \hline
\color{red}{3} & \color{blue}{5} &　\color{blue}{イ}　\\ \hline
\color{red}{3} & \color{blue}{6} &　\color{blue}{イ}　\\ \hline
\color{red}{4} & \color{blue}{5} &　\color{blue}{イ}　\\ \hline
\color{red}{4} & \color{blue}{6} &　\color{blue}{イ}　\\ \hline
\color{blue}{5} & \color{blue}{6} &　\color{magenta}{ウ}　\\ \hline
\end{array}\)

の\(\,15\,\)通りが等しく起こり得ます。

よって、

ア　
\(\,2\,\)人とも男子が選ばれる確率は

　\(\displaystyle \color{red}{\frac{6}{15}}\)

イ
男子と女子が1人ずつ選ばれる確率は

　\(\displaystyle \color{blue}{\frac{8}{15}}\)

ウ
\(\,2\,\)人とも女子が選ばれる確率は

　\(\displaystyle \color{magenta}{\frac{1}{15}}\)

最も大きいのは男子と女子が\(\,1\,\)人ずつ選ばれる確率で

答え　\(\displaystyle \underline{　イ　\frac{8}{15}　}\)

もちろん樹形図でもかまいませんし、組み合わせを書き出しても良いですよ。
ただし、男子\(\,4\,\)人と女子\(\,2\,\)人は区別するのを忘れないでください。

同じ人はこの世に二人といません。

(8)
①
グラフから読み取ります。

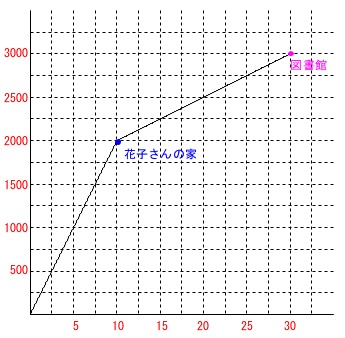
\(\color{black}{\fbox{　あ　}}\)
花子さんの家を出発したのは、太郎さんが自宅を出発して\(\,10\,\)分後、
図書館に到着したのは\(\,30\,\)分後なので、

花子さんの家を出発してから　\(\,\underline{　20　}\,分後　\,\)

\(\color{black}{\fbox{　い　}}\)
太郎さんが自宅を出発して\(\,15\,\)分後、自宅から\(\,2250\,\mathrm{m}\,\)の地点にいます。
図書館までは、\(\,3000\,\mathrm{m}\,\)あるので残りは

　\(\hspace{10pt}3000-2250\\
=\underline{　750　}\,\mathrm{m}\,\)

正確には直線の式を求めて代入しますが、ここではグラフを読み取ります。

②
太郎さんが出発した時刻を基準にして
　弟が主発したのは\(\,10\,\)分後、
　太郎さんに追いついたのは\(\,20\,\)分後
なので、
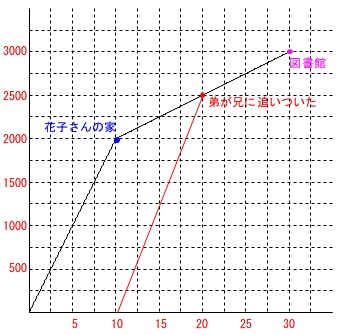\(\,10\,\)分間で\(\,2500\,\mathrm{m}\,\)移動したことになるので、

　\(\displaystyle \frac{2500}{10}=250\,\mathrm{m}/分\)

答え　\(\,毎分　\underline{　250　}　\mathrm{m}\,\)

第２問

\(\color{black}{\fbox{　2　}}\)

データの活用です。
データの種類がいくつかあるので、しっかり見分けておきましょう。

(1)
　通学方法\(\,\mathrm{\color{red}{A}}\,\)は徒歩
　通学方法\(\,\mathrm{\color{blue}{B}}\,\)は自転車やバス

通学方法はこの\(\,2\,\)種類です。

表は具体的な値のデータとそれを度数分布表にしたものです。

ア
範囲は最大値と最小値の差です。

\(\,\mathrm{\color{red}{A}}\,\)の範囲

　\(27-4=\color{red}{23}\)

\(\,\mathrm{\color{blue}{B}}\,\)の範囲

　\(31-10=\color{blue}{21}\)

\(\,\mathrm{\color{blue}{B}}\,\)の範囲の方が小さい。

イ
中央値（メジアン）はデータを小さい順、大きい順に並べたとき、真ん中に来る値のことですが、
データ個数が偶数のときは、真ん中2つの平均を中央値とします。

⇒　代表値とは？度数分布表の平均値,中央値の求め方と最頻値の答え方

\(\,\mathrm{\color{red}{A}}\,\)の中央値は、\(\,12\,\)番目と\(\,13\,\)番目の平均になります。

　\(\displaystyle \frac{18+19}{2}=\color{red}{18.5}\)

\(\,\mathrm{B}\,\)の中央値は、\(\,8\,\)番目と\(\,9\,\)番目の平均になります。

　\(\displaystyle \frac{18+18}{2}=\color{blue}{18}\)

\(\,\mathrm{\color{blue}{B}}\,\)の方が中央値は小さい。

ウ
最頻値（モード）は同じ値のデータの数が一番多い値のことです。

\(\,\mathrm{\color{red}{A}}\,\)の最頻値は3つの\(\,\color{red}{17}\,\)

\(\,\mathrm{\color{blue}{B}}\,\)の最頻値は3つの\(\,\color{blue}{17}\,\)

最頻値は同じです。

エ
今度は度数分布表を見ます。

\(\,25\,\)分以上\(\,30\,\)分未満の階級の度数は

　\(\,\mathrm{\color{red}{A}}\,\)が\(\,\color{red}{3}\,\)　\(\,\mathrm{\color{blue}{B}}\,\)が\(\,\color{blue}{2}\,\)

\(\,\mathrm{\color{blue}{B}}\,\)の方が度数は小さい。

オ
\(\,15\,\)分未満である階級の相対度数の合計とは、累積相対度数と言われます。
※「累積度数」は\(\,2021\,\)年の新課程教科書から正式採用されます。

⇒　度数分布表とは？階級の幅と階級値および累積度数とヒストグラム

表にするとすぐに分かりますが、累積度数を度数合計で割った値です。

\(\,\mathrm{\color{red}{A}}\,\)の度数分布表

　\(\begin{array}{|c|c|c|c|c|} \hline
　階級　 &　度数　 &　累積度数　&　累積相対度数　\\ \hline
0～5 & 1 & 1 & 0.04 \\ \hline
5～10 & 1 & 2 & 0.08 \\ \hline
10～15 & 2 & 4 & \color{red}{0.17} \\ \hline
15～20 & 10 & 14 & 0.58 \\ \hline
20～25 & 7 & 21 & 0.88 \\ \hline
25～30 & 3 & 24 & 1.00 \\ \hline
30～35 & 0 & 24 & 1.00 \\ \hline
　計　& 24 & &\\ \hline
\end{array}\)

正確には\(\,15\,\)未満の累積相対度数は

　\(\displaystyle \frac{4}{24}=0.1666\cdots\)

\(\,\mathrm{\color{blue}{B}}\,\)の度数分布表

　\(\begin{array}{|c|c|c|c|c|} \hline
　階級　 &　度数　 &　累積度数　&　累積相対度数　\\ \hline
0～5 & 0 & 0 & 0 \\ \hline
5～10 & 0 & 0 & 0 \\ \hline
10～15 & 3 & 3 & \color{blue}{0.19} \\ \hline
15～20 & 6 & 9 & 0.56 \\ \hline
20～25 & 4 & 13 & 0.88 \\ \hline
25～30 & 2 & 15 & 0.81 \\ \hline
30～35 & 1 & 16 & 1.00 \\ \hline
　計　& 16 & & \\ \hline
\end{array}\)

正確には\(\,15\,\)未満の累積相対度数は

　\(\displaystyle \frac{3}{16}=0.1875\)

\(\,\mathrm{\color{blue}{B}}\,\)の方が\(\,15\,\)分未満の累積相対度数は大きい。

答え　\(\,\underline{　ア , イ , エ　}\,\)　

(2)
(1)は\(\,3\,\)年\(\,1\,\)組の\(\,\mathrm{A}\,\)と\(\,\mathrm{B}\,\)の通学方法についてのデータでした。
今度は\(\,3\,\)年\(\,2\,\)組と\(\,3\,\)組のデータを比較します。

①
通学時間の平均値は

　\(\displaystyle (平均値)=\frac{　総通学時間　}{　度数　}\)

なので、通学方法別の平均値と度数をかけた時間を計算しなくてはなりません。

\(\,2\,\)組の\(\,\mathrm{A}\,\)による通学時間の合計は

　\(\hspace{10pt}17.2\times 25=430\)

\(\,2\,\)組の\(\,\mathrm{B}\,\)による通学時間の合計は

　\(\hspace{10pt}21.6\times 15=324\)

よって\(\,2\,\)組の通学時間は総合計時間は

　\(\hspace{10pt}430+324=754\)

なので平均通学時間は

　\(\displaystyle \hspace{10pt}\frac{754}{40}=\color{red}{18.85}\)

これは太郎さんの平均値の求めた

　\(\displaystyle \frac{17.2+21.6}{2}=19.4\)

とは違います。

これは、\(\,\mathrm{A}\,\)で通学している生徒の度数と\(\,\mathrm{B}\,\)で通学している生徒の度数が違うからで、

【理由】をまとめるとすれば、

\(\color{black}{\fbox{　あ　}}\)　\(\,\underline{　ウ　}\,\)　の「人数」と、
\(\color{black}{\fbox{　い　}}\)　\(\,\underline{　オ　}\,\)　の「異なる」が当てはまります。

②
\(\,2\,\)組と同様に\(\,3\,\)組の通学時間の平均値は

\(\,\mathrm{A}\,\)で通学している生徒の通学時間の合計が
　
　\(\hspace{10pt}17.0\times 18=306\)

\(\,\mathrm{B}\,\)で通学している生徒の通学時間の合計が

　\(\hspace{10pt}21.5\times 22=473\)

なので\(\,3\,\)組全体での通学時間合計は

　\(\hspace{10pt}306+473=779\)

よって\(\,3\,\)組の通学時間の平均値は

　\(\displaystyle \frac{779}{18+22}=\color{blue}{19.475}\)

小数第2位を四捨五入して答えにします。

答え　\(\color{black}{\fbox{　ア　}}\)　\(\,\underline{　18.9　}　(分)\,\)　\(\color{black}{\fbox{　イ　}}\)　\(\,\underline{　19.5　}　(分)\,\)

\(\color{black}{\fbox{　1　}}\)　,　\(\color{black}{\fbox{　2　}}\)は以上です。
\(\color{black}{\fbox{　1　}}\)だけで\(\,4\,\)割の配点がされていますよ。

第３問第４問

第３問第４問はページを分けてあります。

⇒　奈良県公立高校入試問題2019年(平成31年)度の数学の解説【後半】

\(\color{black}{\fbox{　3　}}\)は反比例を表す関数の性質と座標問題です。
\(\color{black}{\fbox{　4　}}\)は平行四辺形と折り返し問題です。

難しくはありませんが手を止めたらそこで終わり、というのは応用問題では共通していますよ。

\(\,2018\,\)年度は正方形の折り返しでしたが似ているようで少し違います。

⇒　奈良県公立高校入試の数学の過去問題と解答解説

\(\color{black}{\fbox{　1　}}\)については基本的な小問集合というのは変わりありません。
配点も大きいので確実にとりましょう。