2019年(平成31年度)広島県で行われた公立高校入試の数学の問題と解説です。
問題が1から6まであり、小問に分かれていますが全体の問題量としてはそれほど多いわけではありません。
教科書の内容をしっかり身につけていればそれほど時間もかからないでしょう。
問題は広島県で公開してくれています。
教科書の中にある数学の用語の意味を理解できていれば難しい問題は1つもありません。
会員の目標は\(\,15\,\)分です。
\(\color{black}{\fbox{ 1 }}\)
(1)
正の数負の数の加法減法です。
加減は前から順に計算すれば良いだけです。
\(\hspace{10pt}-7+9-8\\
=2-8\\
=\underline{ -6 }\)
正の数と負の数の加減は数直線で考えると確実ですよ。
 数直線上で足し算は右に、引き算は左に移動するだけです。
数直線上で足し算は右に、引き算は左に移動するだけです。
(2)
文字式の除法です。
割り算は逆数のかけ算、というのは算数も同じで、割る部分が分母にまわります。
\(\hspace{10pt}8x^2\div 4x\\
\displaystyle =8x^2\times \frac{1}{4x}\\
\displaystyle =\frac{8x^2}{4x}\\
\displaystyle =\underline{ 2x }\)
もちろんこの程度は暗算できるでしょうが、
かける数や割る数が増えたややこしい文字式でも同じ方法をとればすべてが同じ作業で終わります。
「これはこれで解けるから」とその場その場の方法でやるからちょっとひねられたら分からなくなるし、遅いのです。
高校でも数学を得点源にしたいなら、高校入試までに基本的な数式処理は身につけておきましょう。
ただ、この程度は暗算できるくらいの練習はやっておいた方が良いですね。
(3)
連立方程式の基本は一文字消去です。
\( \begin{cases}
\hspace{7pt} 2x-y=1\\ \\
\hspace{7pt} -3x+y=2
\end{cases}\)
両辺をそれぞれ加えると\(\,y\,\)が消えますので\(\,x\,\)から求めましょう。
\(\hspace{22pt}2x-y=1\\
\underline{+)-3x+y=2}\\
\hspace{16pt}-x\hspace{16pt}=3\\
\hspace{44pt}x=-3\)
これをどっちの方程式でも良いので代入します。
上の方程式に代入しておきます。
\(\begin{eqnarray}
2(-3)-y&=&1\\
-6-y&=&1\\
-y&=&7\\
y&=&-7
\end{eqnarray}\)
答え \(\,\underline{ x=-3\,,\,y=-7 }\,\)
代入するときは正の数でも負の数でも(かっこ)をつけておくとミスが減りますよ。
連立方程式を解くということは交点を求めることにもなるので、
答えを座標の形で書いても良いです。
\(\,(\,x\,,\,y\,)=\underline{ (\,-3\,,\,-7\,) }\,\)
(4)
無理数の計算です。
分母の有理化と足し算なので基本というより計算ルール通りです。
\(\hspace{10pt}\displaystyle \frac{4}{\sqrt{2}}+\sqrt{18}\\
\displaystyle =\frac{4\times \color{red}{\sqrt{2}}}{\sqrt{2}\times \color{red}{\sqrt{2}}}+\sqrt{\color{blue}{3^2\times 2}}\\
\displaystyle =\frac{4\sqrt{2}}{2}+3\sqrt{2}\\
=2\sqrt{2}+3\sqrt{2}\\
=\underline{ 5\sqrt{2} }\)
ここまでていねいにする必要もありませんが、素因数分解は確実にやっておきましょう。
(5)
球の表面積、体積の公式は中学生では導けませんので『覚えて使う』しかありません。
球の表面積\(\,\mathrm{S}\,\)は半径\(\,r\,\)とすると
\(\color{red}{\large{\mathrm{S}=4\,\pi r^2}}\)
です。
この公式に半径\(\displaystyle\, \frac{1}{3}\,\)を代入すると、
\(\begin{eqnarray}\displaystyle
\mathrm{S}&=&4\,\pi\,\times \left(\frac{1}{3}\right)^2\\
&=&\underline{ \frac{4}{9}\,\pi } (\,\mathrm{cm^2}\,)
\end{eqnarray}\)
この\(\,\pi\,\)は分子にあるので分子に乗せても良いです。
\(\hspace{10pt}\displaystyle \underline{ \frac{4\,\pi}{9} } (\,\mathrm{cm^2}\,)\)
ただし、分母によりすぎて、分母にあるように見える紛らわしい書き方はしないようにしましょう。
(6)
正多角形の内角や外角を求める、利用する問題では外角から求めておく方がはやいです。
\(\,n\,\)角形の内角の和の公式
\(180(n-2)\)
もありますが、外角の和は常に一定で\(\,360\,\)度なのでそれ以上の大きな数値が出ない分楽ですよ。
正五角形の1つの外角は
\(\hspace{10pt} \displaystyle \frac{360^{\circ}}{5}=72^{\circ}\)
これから正五角形の1つの内角は
\(\hspace{10pt}180^{\circ}-72^{\circ}\\
=\underline{ 108^{\circ} }\)
「何度ですか」と聞かれているので、
\(\,\underline{ 180度 }\,\)
と答えておいた方が良いのかな。
解答用紙には単位が付いているかもしれませんが、問題に合わせて単位を書くようにしてください。
(7)
説明はいらないでしょう。
「\(\,y\,\)は\(\,x\,\)に反比例し」
なので
\(\displaystyle y=\frac{\color{red}{a}}{x}\)
となっているはずです。
これが、\(\,(\,x\,,\,y\,)=(-4\,,\,5\,)\,\)を通るので、
\(\begin{eqnarray}\displaystyle
5&=&\frac{a}{-4}\\
-20&=&a
\end{eqnarray}\)
答え \(\displaystyle \underline{ y=-\frac{20}{x} }\)
比例定数\(\,\color{red}{a}\,\)を求めるとき、反比例の関係を
\(xy=a\)
とおいて、
\(a=(-4)\times (5)\)
としても良いですよ。
ただし、\(\,y\,\)を\(\,x\,\)の式で表すように問題が指示していますので、
答えは\(\displaystyle \,y=-\frac{20}{x}\,\)の形にしておきましょう。
(8)
\(\,3\,\)枚の硬貨を同時に投げても、一枚ずつ投げても同じことです。
簡単な樹形図で終わるのでどうでも良いことですけどね。笑
樹形図で良いですが表にしておきます。
表を\(\,○\,\)、裏を\(\,×\,\)で表します。
\(\begin{array}{|c|c|c|c|} \hline
1枚目 & 2枚目 & 3枚目 & \\ \hline
○ & ○ & ○ & \\ \hline
○ & ○ & × & \\ \hline
○ & × & ○ & \\ \hline
○ & × & × & \color{red}{●} \\ \hline
× & ○ & ○ & \\ \hline
× & ○ & × & \color{red}{●} \\ \hline
× & × & ○ & \color{red}{●} \\ \hline
× & × & × & \\ \hline
\end{array}\)
答え \(\displaystyle \underline{ \frac{3}{8} }\)
\(\color{black}{\fbox{ 2 }}\)
(1)
同じ長さの弧に対する円周角は等しくなります。
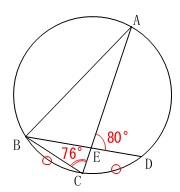
条件は
\(\,\stackrel{\large{\frown}}{\mbox{BC}}=\stackrel{\large{\frown}}{\mbox{CD}}\,\)
\(∠\mathrm{ACB}=76^{\circ}\)
\(∠\mathrm{AED}=80^{\circ}\)
が与えられています。
\(\,\stackrel{\large{\frown}}{\mbox{BC}}=\stackrel{\large{\frown}}{\mbox{CD}}\,\)
なので
\(\,\mathrm{\color{blue}{∠BAC}=\color{blue}{∠CBD}}\,\)
また、
\(∠\mathrm{AED}=80^{\circ}\)
から
\(\,\mathrm{∠AEB=\color{blue}{100^{\circ}}}\,\)
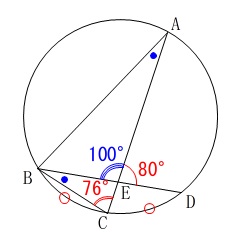 なので
なので
\(\begin{eqnarray}
∠\mathrm{CBE}&=&∠\mathrm{BAC}\\
&=&\color{blue}{100^{\circ}}-\color{red}{76^{\circ}}\\
&=&24^{\circ}
\end{eqnarray}\)
よって、
\(\begin{eqnarray}
∠\mathrm{ABE}&=&80^{\circ}-24^{\circ}\\
&=&\underline{ 56^{\circ} }
\end{eqnarray}\)
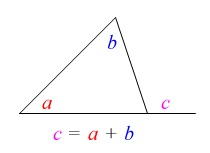
三角形の内角の和でも良いですが、
ここでは1つの外角は他の2つの内角の和に等しいということを利用しています。
(2)
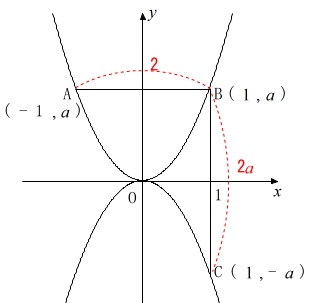
放物線が2つあり、\(\,\mathrm{AB}\,\)と\(\,\mathrm{BC}\,\)は軸に平行です。
点\(\,\mathrm{B}\,\)の\(\,x\,\)座標が\(\,1\,\)
\(\displaystyle \,\mathrm{AB+BC=\frac{16}{3}}\,\)
 ということから比例定数\(\,a\,\)を求めます。
ということから比例定数\(\,a\,\)を求めます。
座標を書き出すと、点\(\,\mathrm{B}\,\)の\(\,x\,\)座標が\(\,1\,\)なので
\(\,\mathrm{B}\,(\,1\,,\,a\,)\,\)
\(\,\mathrm{A}\,\)と\(\,\mathrm{B}\,\)は\(\,y\,\)軸対称なので\(\,y\,\)座標が同じで、
\(\,\mathrm{A}\,(\,-1\,,\,a\,)\,\)
\(\,\mathrm{C}\,\)と\(\,\mathrm{B}\,\)は\(\,x\,\)軸対称なので\(\,x\,\)座標が同じで
\(\,\mathrm{C}\,(\,1\,,\,-a\,)\,\)
ここで1つチェックしておきましょう。
問題にも書かれていますが\(\,\mathrm{A,B}\,\)が\(\,y=ax^2\,\)上の点なので、
比例定数\(\,a\,\)は正の数です。
よって、
\(\begin{eqnarray}\displaystyle
\mathrm{AB+BC}&=&\frac{16}{3}\\
\color{red}{2}+\color{red}{2a}&=&\frac{16}{3}\\
2a&=&\frac{16}{3}-\color{red}{2}\\
&=&\frac{10}{3}\\
a&=&\underline{ \frac{5}{3} }
\end{eqnarray}\)
(3)
\(\,9\,\)人の中央値が求まるので、そこからです。
⇒ 代表値とは?度数分布表の平均値,中央値の求め方と最頻値の答え方
代表値については何度も確認しておきましょう。
\(\,9\,\)人のデータを小さい順に並べると、
\(29,30,31,31,\color{red}{32},35,36,48,52\)
小さい方からでも大きい方からでも\(\,5\,\)番目の人の値\(\,\color{red}{32}\,\)が中央値になります。
\(\,10\,\)人目のデータを加えると中央値が\(\,1\mathrm{kg}\,\)増加するので、
中央値が\(\,33\mathrm{kg}\,\)になることになります。
\(\,10\,\)人のデータの中央値は両端から\(\,5\,\)番目と\(\,6\,\)番目の人の値の平均なので、
\(\,\mathrm{C}\,\)さんは小さい方から\(\,6\,\)番で、
\(\,5\,\)番目の値\(\,32\,\)との平均が\(\,33\,\)になれば良いので、
\(\begin{eqnarray}\displaystyle
\frac{\mathrm{C}+32}{2}&=&33\\
\mathrm{C}+32&=&33\times 2\\
\mathrm{C}&=&66-32\\
&=&\underline{ 34 } \mathrm{kg}
\end{eqnarray}\)
ここまでで配点で\(\,25\,\)点あります。
といっても、満点が\(\,50\,\)点ですので\(\,50\,\)%です。
この後も誘導がしっかりされているので難しい問題はありませんが、
『覚え太郎』程度の教科書レベルの基本用語はすべて覚えておきましょう。
\(\color{black}{\fbox{ 3 }}\)はよくある花だんに道を通す問題ですが、
平方根の求め方の基本が問題として組まれています。
その後も基本問題が並びますが、
基本用語を覚えていないと考えても答えは出て来ません。
更新が不定期なのでまとめページでも更新確認しておいてください。
