広島県で行われた公立高校入試2019年（平成31年度）の数学の問題と解説の後半部分です。
前半は問1問2だけになりましたが後半問3から問6まで一気に解説します。
ややこしそうに見えて実は基本問題となっている問題が多いので、問題文から条件を読み取ることがポイントです。
問題は広島県で公開してくれています。
\(\color{black}{\fbox{ 1 }}\) \(\color{black}{\fbox{ 2 }}\)までで配点の半分あるので見直しをしてから先に進むと良いですよ。
\(\color{black}{\fbox{ 3 }}\)からは思いついた方針で値を求めるのではなく、考え方を問題に合わせる必要があります。
穴埋め問題もあるので条件の読み取りと問題の指示に従って進めることがポイントです。
\(\color{black}{\fbox{ 3 }}\)
説明の文字が多いので読むのに時間がかかるかもしれませんが、
条件だけ抜き出してみると問題自体は簡単です。
花壇でも畑でも同じで、長方形の中に道を縦横に通し等しく\(\,4\,\)分割します。
1つは場所①
\(\,6\,\mathrm{m}\times 9\,\mathrm{m}\,\)の長方形を\(\,10\,\mathrm{m^2}\,\)の長方形4つに分けます。
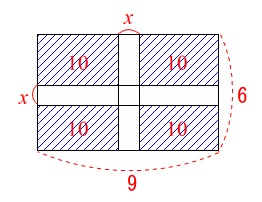
もう一つは場所②
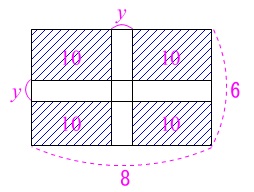
\(\,6\,\mathrm{m}\times 8\,\mathrm{m}\,\)の長方形を\(\,10\,\mathrm{m^2}\,\)の長方形4つに分けます。
このときの間に通す道幅を求めます。
(1)
場所①について道幅を求めます。
元の長方形の面積は
\(6\times 9=54\,\mathrm{m^2}\)
これを\(\,\mathrm{10\,m^2}\,\)4つに分割するので、
通す道が使う面積は
\(54-10\times 4=\color{magenta}{14} \,\mathrm{m^2}\)
となります。
道の幅を\(\,x\,\)とすると、道の占める面積は、
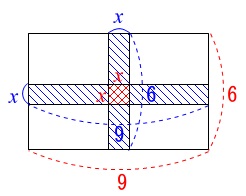横の長方形が
\(9\times x=\color{blue}{9x}\)
縦の長方形が
\(6\times x=\color{blue}{6x}\)
ただし、重なる編み目部分\(\,\color{red}{x^2}\,\)は2回求めていることになるので1回分引いた値が通す道の面積になります。
よって、成り立つ関係式は
\(\begin{eqnarray}
\color{blue}{9x}+\color{blue}{6x}-\color{red}{x^2}&=&\color{magenta}{14}\\
-x^2+15x-14&=&0\\
x^2-15x+14&=&0
\end{eqnarray}\)
答え \(\color{black}{\fbox{ ア }}\) \(\,\underline{ 15 }\,\) \(\color{black}{\fbox{ イ }}\) \(\,\underline{ 14 }\,\)
この\(\,2\,\)次方程式を解けば道幅が求まりますが、
当然、道幅が土地の横、縦より大きくなるわけはないので
\(0\,＜\,x\,＜\,6\)
と考えられます。
\(\begin{eqnarray}
x^2-15x+14&=&0\\
(x-1)(x-14)&=&0\\
x&=&1\,,\,14
\end{eqnarray}\)
より、\(\,x=1\,\)が適する解です。
答え \(\color{black}{\fbox{ ウ }}\) \(\,\underline{ 1 }\)
この問題のように間に道を通す問題では、道を端によせる方法が普通です。
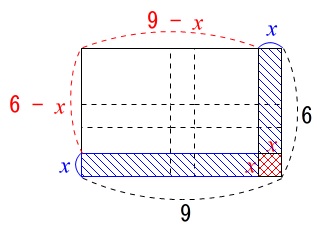すると道を除いた長方形の面積が\(\,\color{magenta}{40}\,\mathrm{m^2}\)であることから、
\(\begin{eqnarray}
(\color{red}{9-x})(\color{red}{6-x})&=&\color{magenta}{40}\\
54-15x+x^2&=&40\\
x^2-15x+14&=&0
\end{eqnarray}\)
と同じ方程式が導けます。
この程度の問題だと思い立った方法で突っ走った方がはやいのでどちらでも良いですよ。
ただし、問題にあった方程式が出てこなければ何かが違っているということです。笑
(2)
場所②についても同じように方程式を立てることができます。
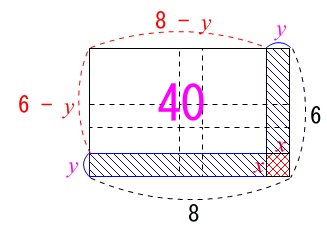
\(\begin{eqnarray}
(8-y)(6-y)&=&40\\
48-14y+y^2&=&40\\
y^2-14y+8&=&0
\end{eqnarray}\)
左辺は因数分解できませんので解の公式です。
\(\begin{eqnarray}\displaystyle
y&=&\frac{14\pm \sqrt{14^2-4\times 1\times 8}}{2}\\
&=&\frac{14\pm \sqrt{196-32}}{2}\\
&=&\frac{14\pm \sqrt{164}}{2}\\
&=&\frac{14\pm 2\sqrt{41}}{2}\\
&=&7\pm \sqrt{41}
\end{eqnarray}\)
この場所②においても道幅には制限があります。
\(\,0\,＜\,y\,＜\,6\)
なので、
\(y=7-\sqrt{41}\)
ここまでは問題が解いてくれています。
問題はここから始まりますが、花だんの面積とは余り関係がありません。
平方根の求め方の基本です。
\(\sqrt{41}\)の小数第\(\,1\,\)位を求めます。
先ず整数部分が\(\,6\,\)だということは、
\(\begin{eqnarray}
\sqrt{36}＜&\sqrt{41}&＜\sqrt{49}\\
6＜&\sqrt{41}&＜7
\end{eqnarray}\)
から分かります。
次に小数第\(\,1\,\)位ですが、
\(6.1^2=37.21\)
\(6.2^2=38.44\)
のように\(\,6.1\,\)と\(\,6.2\,\)から始めても良いのですが、
中間あたりの\(\,6.5\,\)から始めて検討をつけた方が早いです。
\(6.5^2=42.25\)
これは\(\,41\,\)を超えているので逆に、小さい数の平方を計算してみます。
\(6.4^2=40.96\)
これは\(\,41\,\)より小さいので
\(\begin{eqnarray}
40.96\,＜&\,41\,&＜\,42.25\\
6.4^2\,＜&\,41\,&＜\,6.5^2
\end{eqnarray}\)
正の数の大小なので平方根の大小も同じです。
\(6.4\,＜\,\sqrt{41}\,＜\,6.5\)
つまり、
\(\sqrt{41}=6.4\cdots\)
答え \(\color{black}{\fbox{ エ }}\) \(\,\underline{ 4 }\,\)
小数第\(\,2\,\)位も同じように計算すると、
\(6.40^2=40.96\)
\(6.41^2=41.0881\)
なので
\(\sqrt{41}=6.40\cdots\)
このことから\(\,\sqrt{41}=6.4\,\)として道幅を求めると
\(\begin{eqnarray}
y&=&7-\sqrt{41}\\
&=&7-6.4\\
&=&0.6
\end{eqnarray}\)
答え \(\color{black}{\fbox{ オ }}\) \(\,\underline{ 0.6 }\,\)
\(\color{black}{\fbox{ 3 }}\)は以上です。
\(\color{black}{\fbox{ 4 }}\)
\(\,2\,\)ページに渡る問題ですが、中点連結定理とひし形の定理を利用するだけです。
【課題】があります。
辺\(\,\mathrm{ＡＢ}\,\)と線分\(\,\mathrm{ＡＤ}\,\)の中点をそれぞれ\(\,\mathrm{Ｅ,Ｆ}\,\)とします。
このとき、四角形\(\,\mathrm{ＥＤＣＦ}\,\)はどのような形になるでしょうか。
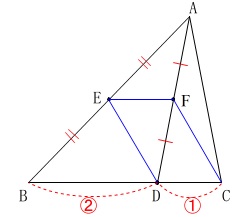
条件を図示すればすぐに平行四辺形だということはわかりますが、
(1)はそれを証明します。
条件を抜き出して見ます。
\(\,\mathrm{\color{blue}{ＢＤ=2ＣＤ}}\,\)
\(\,\mathrm{E,F}\,\)は\(\,\mathrm{AB,AD}\,\)の中点
条件はこれだけです。
\(\,\mathrm{E,F}\,\)は\(\,\mathrm{AB,AD}\,\)の中点
から中点連結定理につながらない人は、中学数学の基本用語が抜け落ちすぎです。
他の分野でも用語のチェックをしておいた方が良いですね。
上田さんと高橋さんの書いた図の違いは、鋭角三角形か鈍角三角形化の違いだけです。
中点連結定理は鋭角三角形でも鈍角三角形でも成り立つのでどちらか1つを見ておけば良いですよ。
(1)は簡単に終わりますのでこのまま証明に入ります。
証明するときは図の中で証明を終わらせておくというのは基本中の基本ですよ。
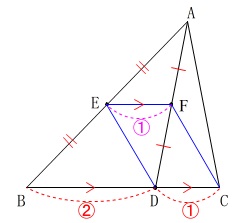
〔 証明 〕
点\(\,\mathrm{E}\,\)は辺\(\,\mathrm{AB}\,\)の中点、点\(\,\mathrm{F}\,\)は線分\(\,\mathrm{AD}\,\)の中点だから,
(ここからが答えになります。）
中点連結定理により
\(\,\mathrm{EF}\, /\!/\,\mathrm{BD}\,\)
\(\displaystyle \mathrm{EF}=\frac{1}{2}\,\mathrm{BD}\)
また
\(\,\mathrm{ＢＤ=2ＣＤ}\,\)
であるから
\(\displaystyle \mathrm{DC}=\frac{1}{2}\,\mathrm{BD}\)
よって、
\(\,\mathrm{EF=DC}\,\)
以上のことから、
\(\,1\,\)組の対辺が平行で等しい
ので
四角形\(\,\mathrm{EDCF}\,\)は平行四辺形である。
（おわり）
辺について「等しい」というのは「長さが等しい」ということなので、
「長さが等しい」とは書かなくても通用しますが、書いていても問題はありません。
(2)
(1)の条件に何を加えれば四角形\(\,\mathrm{EDCF}\,\)がひし形になるか？
という問題です。
鋭角三角形でも鈍角三角形でも成り立つことを課題にしてあるので、
見やすい方の図だけで考えて良いですよ。
ひし形になる条件はいくつかあります。
ただし、この問題では辺が4つ指定してあって、その中から2つを選ぶので問題の答えの中から探っても答えは出ます。
ここでは、ひし形になる条件から2つを選びましょう。
「四角形\(\,\mathrm{EDCF}\,\)がひし形になるには」
ということですが、逆に、
「四角形\(\,\mathrm{EDCF}\,\)がひし形なら」
と考えると早いです。
ひし形は4つの辺が等しい平行四辺形であり、対角線が垂直に交わります。
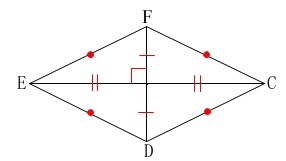つまり、この問題では
\(\,\mathrm{AD}\,\) ⊥ \(\,\mathrm{EC}\,\)
が言えれば良いのです。
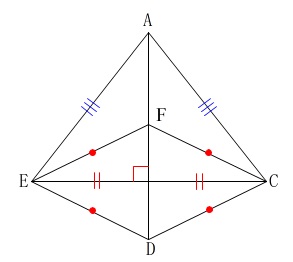このとき、
直線\(\,\mathrm{AD}\,\)は底辺\(\,\mathrm{EC}\,\)を垂直に\(\,2\,\)等分している
ことから、
\(\,\mathrm{△AEC}\,\)および\(\,\mathrm{△FEC}\,\)は二等辺三角形
です。
等しい辺はいくつか組が考えられますが、問題の選択肢から、
\(\,\mathrm{AE=AC}\,\)
答え \(\color{black}{\fbox{ ア }}\) \(\color{black}{\fbox{ イ }}\) \(\,\underline{ ②,④ }\,\)
（順序はどちらでもいいですが、2つとも合っていて正解です。）
中線が直交していれば\(\,\mathrm{△AFC}\,\)は二等辺三角形になり、
四角形\(\,\mathrm{EDCF}\,\)がひし形になる、ということです。
\(\color{black}{\fbox{ 4 }}\)は以上です。
\(\color{black}{\fbox{ 5 }}\)
\(\color{black}{\fbox{ 5 }}\)は問題の条件を身逃さなければ、
単に折り返しただけで、三平方の定理を利用すればすぐに答えが出る問題です。
折り返しでは、折り返される前と後の辺と角は等しいので図に書き込みましょう。
条件
\(\,\mathrm{△ABC}\,\)は\(\,\mathrm{AB=BC=6}\,\)の直角二等辺三角形。
頂点\(\,\mathrm{A}\,\)が\(\,\mathrm{BC}\,\)の中点\(\,\mathrm{M}\,\)に重なるように折り返す。
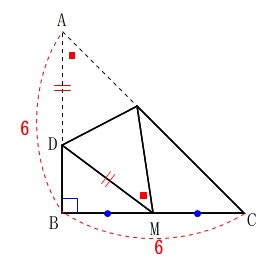求めたいのは\(\,\mathrm{BD}\,\)の長さです。
線分\(\,\mathrm{BD}\,\)の長さを\(\,\color{red}{x}\,\)とすると、
\(\,\mathrm{AD=DM}=\color{blue}{6-x}\,\) \((\,0＜x＜6\,)\)
（折り返した点が\(\,\mathrm{BC}\,\)の中点にあることから\(\,(\,0＜\,x\,＜\,3\,)\,\)としても良いです。）
また\(\,\mathrm{M}\,\)は\(\,\mathrm{BC}\,\)の中点なので
\(\,\mathrm{BM=\color{magenta}{3}}\,\)
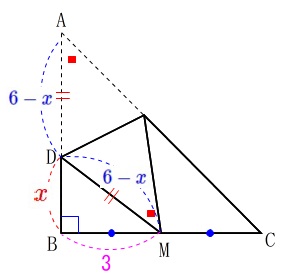直角三角形\(\,\mathrm{BDM}\,\)に三平方の定理を用いて、
\(\begin{eqnarray}\displaystyle
\mathrm{BD^2+BM^2}&=&\mathrm{DM^2}\\
\color{red}{x}^2+\color{magenta}{3}^2&=&(\color{blue}{6-x})^2\\
x^2+9&=&36-12x+x^2\\
12x&=&27\\
x&=&\frac{27}{12}\\
&=&\underline{ \frac{9}{4} } （適）
\end{eqnarray}\)
\(\color{black}{\fbox{ 5 }}\)は以上です。
\(\color{black}{\fbox{ 6 }}\)
\(\color{black}{\fbox{ 6 }}\)は比例の関数と1次関数と格子点の問題です。
格子点とは\(\,x,y\,\)座標の両方が整数の点のことですが、
ここでは解説に使うので今だけ覚えておいてください。
グラフと関数が与えられています。
\(y=ax \,(\,a\,＞\,0\,) ･･･①\)
\(\displaystyle y=-\frac{2}{3}\,x+4 ･･･②\)
①②の交点が\(\,\mathrm{A}\,\)
②と\(\,y\,\)軸との交点が\(\,\mathrm{B}\,\)
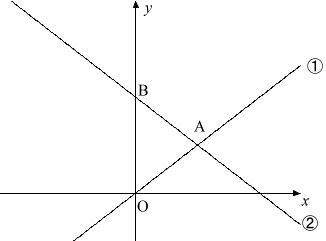
(1)
点\(\,\mathrm{B}\,\)は②において\(\,x=0\,\)のときの座標を表すので、
点\(\,\mathrm{B}\,\)の\(\,y\,\)座標は
\(\displaystyle y=-\frac{2}{3}\,x+4\)
の切片\(\,4\,\)です。
答え \(\,y=\underline{ 4 }\,\)
(2)
線分\(\,\mathrm{OA}\,\)上の格子点が、
原点以外に1つだけ
になる\(\,a\,\)の値で最も小さいものを求めます。
格子点問題では格子点を書き込むと分かり易くなりますよ。
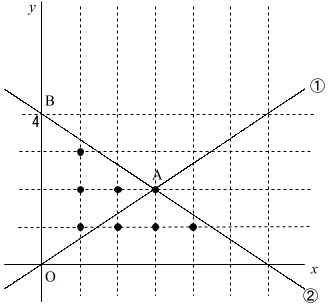軸上にも格子点は存在しますが、
線分\(\,\mathrm{OA}\,\)上の格子点が1つの場合を考えるので必要ありません。
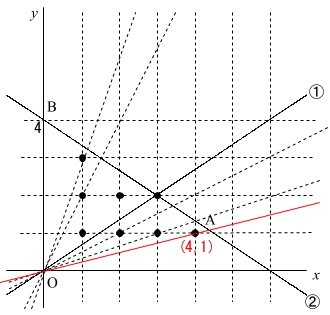線分\(\,\mathrm{OA}\,\)上の格子点が1つになる場合で、
\(\,a\,\)が最も小さい場合、つまり比例定数が一番小さいのは、
\(\,(\,4\,,\,1\,)\,\)
を通るときで、この点を\(\,y=ax\,\)に代入して
\(\begin{eqnarray}\displaystyle
1&=&a\times 4\\
a&=&\underline{ \frac{1}{4} }
\end{eqnarray}\)
\(\,2019\,\)年の広島県公立高校入試の数学は以上です。
前半の\(\color{black}{\fbox{ 1 }}\)、\(\color{black}{\fbox{ 2 }}\)で配点の半分ありますので、
前半\(\,2\,\)問を素早く、確実に処理して後半をじっくり攻略するといいです。
⇒ 2020年(令和2年)広島県公立高校入試の数学の問題と解説
\(\,2020\,\)年度は平均点が割と上がりました。
他の年度も解説しておきますので傾向を確認しておくと良いですね。
クラブ活動で忙しい！
塾に通っているのに数学が苦手！
数学の勉強時間を減らしたい！
数学の勉強方法が分からない！
その悩み、『覚え太郎』が解決します！！！
