愛知県で2019年（平成31年度）に行われた公立校入試B日程数学の問題と解説です。
A日程と問題構成は同じで大問3つで構成されていますが、3問とも小問がつながっているわけではありませんので分からくなったら先に進むと良いです。
この問題への解説は不足しているかもしれませんので、基本的な解き方はA日程の解説を参考にして下さい。
愛知県の公表している問題です。
ここでは、当会の教材を使い込んでいる会員向けとして短時間で解いている方法を書いておきます。
記述解答として解説を入れますが参考にならなかったらすみません。
（けっして解説がめんどくさっ！というわけではありませんのでご理解下さい。）
目標は\(\,20\,\)分ですが、はやい人は\(\,15\,\)分くらいで見直しに入れるでしょう。
誰でもミスはあります。必ず見直しはしましょう。
\(\,\large{1}\,\)
(1)
計算順序に注意しておきましょう。
\(\hspace{10pt} 10-4\div (-2)\\
=10+2\\
=\underline{ 12 }\)
(2)
割り算は逆数のかけ算です。
\(\hspace{10pt}\displaystyle \frac{2}{3}\div \left(-\frac{4}{3}\right)^2\\
\displaystyle =\frac{2}{3}\times \frac{9}{16}\\
\displaystyle =\underline{ \frac{3}{8} }\)
(3)
ルートの中を簡単にすれば中はすべて同じです。
\(\hspace{10pt} \sqrt{32}-\sqrt{8}-\sqrt{2}\\
=4\sqrt{2}-2\sqrt{2}-\sqrt{2}\\
=\underline{ \sqrt{2} }\)
(4)買い物に行って下さい。
\(\,3\,\)割引は定価に\(\,0.7\,\)をかけた値段になります。
定価を\(\,x\,\)とするとハンカチ\(\,1\,\)枚の価格は\(\,0.7x\,\)なので,
おつりとの関係式から
\(\begin{eqnarray}
880&=&2000-0.7x\times 2\\
8800&=&20000-14x\\
14x&=&20000-8800\\
&=&11200\\
x&=&\underline{ 800 } (円)
\end{eqnarray}\)
(5)
『交点』、『共有点』は連立です。
\( \begin{cases}
\hspace{7pt} y=-x+2\\ \\
\hspace{7pt} y=2x-7
\end{cases}\)
この連立方程式を解いて、
\(\begin{eqnarray}
-x+2&=&2x-7\\
-3x&=&-9\\
x&=&3
\end{eqnarray}\)
このとき
\(\begin{eqnarray}
y&=&-(3)+2\\
&=&-1
\end{eqnarray}\)
よって交点の座標は
\(\underline{ (\,3\,,\,-1\,) }\)
座標を聞かれているので\(\,x,y\,\)座標とも出すのを忘れないようにしましょう。
(6)
正の数の大小なので\(\,2\,\)乗しても大小関係は変わりません。
\(8.2\,＜\,\sqrt{n+1}\,＜\,8.4\\
8.2^2\,＜\,n+1\,＜\,8.4^2\\
67.42\,＜\,n+1\,＜\,70.56\\
66.42\,＜\,n\,＜\,69.56\)
よって、\(\,\underline{ 67\,,\,68\,,\,69 }\,\)
(7)
値域が負の範囲にあるので比例定数は負の数です。
軸から遠い\(\,x=4\,\)のとき最小値は\(\,y=-4\,\)となるので、
\(\begin{eqnarray}\displaystyle
-4&=&a\times (4)^2\\
-4&=&16a\\
a&=&\underline{ -\frac{1}{4} }
\end{eqnarray}\)
(8)
樹形図でもたかが\(\,20\,\)通りです。
説明は不要でしょうが、置き場はふたつです。
2つの数字の取り出し方は\(\,5\times 4=20\,\)通り。
\(a-b=2\)
となる組み合わせは
\((\,a\,,\,b\,)=(\,3\,,\,1)\,,\,(\,4\,,\,2\,)\,,\,(\,5\,,\,3\,)\)
の\(\,3\,\)通りだけです。
よって、\(\displaystyle \underline{ \frac{3}{20} }\)
(9)
円に内接する四角形の対角の和は\(\,180°\,\)です。
弧\(\,\stackrel{\large{\frown}}{\mbox{ABC}}\,\)の中心角が\(\,\mathrm{∠AOC=94^{\circ}}\,\)なので、
円周角は\(\,47°\,\)
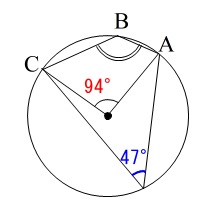よって
\(\begin{eqnarray}
\mathrm{∠ABC}&=&180^{\circ}-47^{\circ}\\
&=&\underline{ 133^{\circ} }
\end{eqnarray}\)
もちろん、反対側の中心角は
\(360-94=266\)
なので、中心角\(\,266°\,\)に対する円周角として求めて同じ程度の計算です。
（こっちが普通です。）
ふっ、と四角形を円に内接させたくなったのでそのまま解説としました。
\(\,\large{1}\,\)は終わりですが『覚え太郎』の範囲で十分でしょう。
次行きます。
\(\,\large{2}\,\)
(1)
ここでの方法は『発展レポート』に書いてある内容になります。
『覚え太郎』会員で思い出せない人は『\(\,2\,\)次方程式』を読み直して下さい。
方程式
\(x^2+ax+15=0\)
の1つの解が\(\,-3\,\)であることからもう一つの解は、
\(\,x=-5\,\)
なので、
\(\begin{eqnarray}
-a&=&(-3)+(-5)\\
a&=&\underline{ 8 }
\end{eqnarray}\)
また、このもう1つの解\(\,x=-5\,\)が方程式
\(2x+a+b=0\)
の解になるので、\(\,a=8\,\)であることから
\(\begin{eqnarray}
2(-5)+(8)+b&=&0\\
b&=&\underline{ 2 }
\end{eqnarray}\)
普通は方程式の解が\(\,x=-3\,\)だということから、
\(\,2\,\)次方程式に代入して\(\,a\,\)を求める、で良いですよ。
今回だけは『覚え太郎』を読み込んでくれている人向けに書いているのでチンタラ説明しません。
次に行きます。
(2)
代表値についての説明は必要ないでしょう。
⇒ 代表値とは？度数分布表の平均値,中央値の求め方と最頻値の答え方
最頻値は \(a=\,\underline{ 4 } 冊\,\)
中央値は、
\(\,4\,\)冊以下の度数合計が\(\,15\,\)人
\(\,5\,\)冊以上の度数合計が\(\,15\,\)人
となっているので、
\(\,4\,\)冊と\(\,5\,\)冊の平均値
\(b=\,\underline{ 4.5 } 冊\,\)
が中央値になります。
さらに、\(\,\mathrm{A}\,\)さんの借りた本の冊数を訂正し平均値を出すと
「平均値が\(\,0.1\,\)上がる」
らしいので、度数合計が\(\,30\,\)だから
訂正後は\(\,3\,\)冊多くなる
ことが分かります。
中央値が変わらなかったことから、
訂正前と訂正後で\(\,4\,\)冊と\(\,5\,\)冊をまたぐことはないので
\(\,\mathrm{A}\,\)さんの借りた本の冊数の訂正の変化は
\(\,1\,\)冊から\(\,4\,\)冊に\(\,3\,\)冊増える
または
\(\,5\,\)冊から\(\,8\,\)冊に\(\,3\,\)冊増える
しかありません。
ヒストグラムを見ると、\(\,1\,\)冊借りた人は度数が\(\,1\,\)で、
\(\,\mathrm{A}\,\)さんが\(\,1\,\)冊から\(\,4\,\)冊に訂正されると範囲が変わってしまう。
よって、\(\,\mathrm{A}\,\)さんが実際に借りた本の冊数は
\(c=\,\underline{ 8 } 冊\,\)
次に行きます。
(3)
格子点の問題です。
グラフで確認しながら進めれば良いですよ。
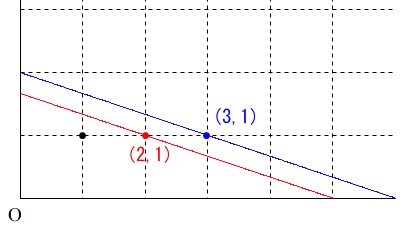含む点は黒い点\(\,●\,\)と赤い点\(\,\color{red}{●}\,\)の\(\,2\,\)個です。
青い点\(\,\color{blue}{●}\,(\,3\,,\,1\,)\)を含むと\(\,3\,\)個目になるので切片は、
\((\,2\,,\,1\,)\)を通るときより大きく
\((\,3\,,\,1\,)\)を通るとき以下
であれば条件を満たします。
\((\,2\,,\,1\,)\)を通るとき
\(\begin{eqnarray}
1&=&-\frac{1}{3}\times (2)+b\\
b&=&\frac{5}{3}
\end{eqnarray}\)
\((\,3\,,\,1\,)\)を通るとき
\(\begin{eqnarray}
1&=&-\frac{1}{3}\times (3)+b\\
b&=&2
\end{eqnarray}\)
より
\(\hspace{10pt}\displaystyle \underline{ \frac{5}{3}\,＜\,b\,≦\,2 }\)
境界は含まないので\(\,(\,3\,,\,1\,)\,\)を通っても良いのです。
(4)
\(\,2019\,\)年の\(\,\mathrm{A}\,\)日程にも同じような問題が出ているので詳しい説明はいらないでしょう。
①
定義域によって傾きが変わる直線です。
\(\,y\,\)の単位は「万」なので座標で表すとき注意しておきましょう。
ⅰ)
\(\,0≦x≦30\,\)のとき\(\,y=20\,\)で一定。
ⅱ)
\(\,30≦x≦60\,\)のとき、
\(\,1\,\)冊増えるごとに\(\,5000\,\)円増えるので、
\(\,(\,30\,,\,20\,)\,,\,(\,60\,,\,35\,)\,\)を通る直線
となるので関数にすると
\(\displaystyle \,\color{red}{y=\frac{1}{2}x＋5}\,\)
ⅲ)\(\,60≦x≦100\,\)のとき
\(\,1\,\)冊増えるごとに\(\,2500\,\)円増えるので、
\(\,(\,60\,,\,35\,)\,,\,(\,100\,,\,45\,)\,\)を通る直線
となるので関数にすると
\(\displaystyle \,\color{blue}{y=\frac{1}{4}x＋20}\,\)
ⅰ)ⅱ)ⅲ)をつなげれば答えです。
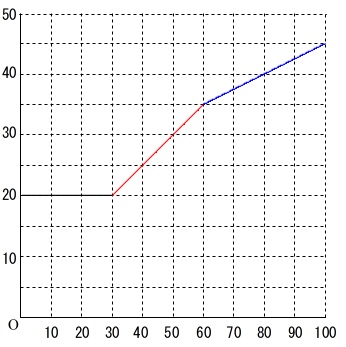
②
段階別に料金の設定がないとすると、
\(\,1\,\)冊\(\,5000\,\)円で作成すると関数は、
\(y=5x\)（\(\,y\,\)の単位は「万」です。）
これは\(\,(\,80\,,\,40\,)\,\)を通るのでグラフを書き込むと
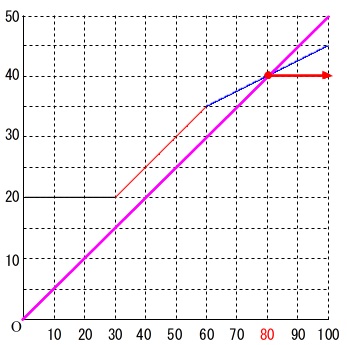冊数によって料金設定のあるグラフが下になる部分が答えになります。
よって、
\(\underline{ 80 冊以上}\)
\(\,80\,\)冊ちょうどのときは同じ料金です。
問題は「\(\,5000\,\)円以下」なので含ませて良いですよ。
\(\,\large{2}\,\) は以上です。
最後の\(\,\large{3}\,\)に進みましょう。
\(\,\large{3}\,\) は平面図形の総合問題ですが、(1)(2)(3)は別問題です。
(1)
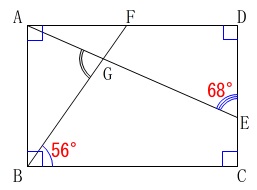
条件
長方形\(\,\mathrm{ABCD}\,\)
\(\,\mathrm{∠GED=68^{\circ}}\,\)
\(\,\mathrm{∠GBC=56^{\circ}}\,\)
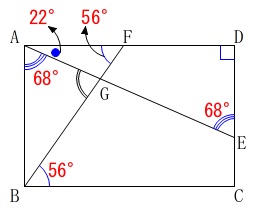
平行線の錯角は等しいので
\(\mathrm{∠AFG=56^{\circ}}\)
\(\mathrm{∠BAG=68^{\circ}}\)
長方形の1つの内角は\(\,90°\,\)なので
\(\mathrm{∠GAF=22^{\circ}}\)
よって、
\(\begin{eqnarray}
\mathrm{∠AGB}&=&56^{\circ}+22^{\circ}\\
&=&\underline{ 78^{\circ} }
\end{eqnarray}\)
長方形は平行四辺形ですよ。
(2)
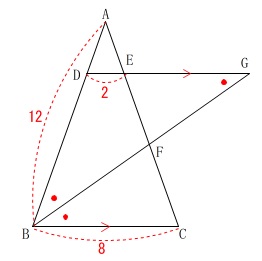
条件
\(\,\mathrm{AB=AC}\,\)
\(\,\mathrm{DE}\, /\!/ \,\mathrm{BC}\,\)
\(\,\mathrm{BG}\,\)は\(\,\mathrm{∠ABC}\,\)の二等分線
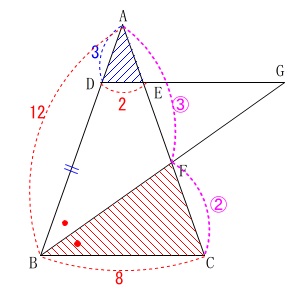
\(\,\mathrm{AB=12}\,\)
\(\,\mathrm{BC=8}\,\)
\(\,\mathrm{DE=2}\,\)
から\(\,\mathrm{△DGB}\,\)は
\(\mathrm{\color{red}{∠DBG=∠DGB}}\)
の二等辺三角形になります。
①
\(\,\mathrm{△ADE}\,\) ∽ \(\,\mathrm{△ABC}\,\)
で相似比は\(\,2：8＝1：4\,\)だから
\(\,\mathrm{AD=3\,,\,DB=9}\,\)
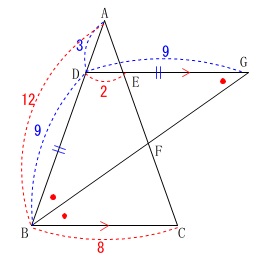\(\,\mathrm{△DGB}\,\)は二等辺三角形で、
\(\,\mathrm{DB=DG}\,\)なので
\(\,\mathrm{DG}=\underline{ 9 }\,\)
②
\(\,\mathrm{BF}\,\)が\(\,\mathrm{∠ABC}\,\)の角の二等分線なので、
\(\begin{eqnarray}
\mathrm{AB:BC}&=&\mathrm{AF:CF}\\
&=&12:8\\
&=&\color{magenta}{3:2}
\end{eqnarray}\)
（『超え太郎』カード－「相似な図形」\(\,\mathrm{No.45}\,\)で確認しておいて下さい。）
このことから\(\,\mathrm{△ABC}\,\)の面積を\(\,1\,\)とすると、
\(\displaystyle \mathrm{△BCF}=\color{red}{\frac{2}{5}}\)
また、\(\,\mathrm{△ABC}\,\) ∽ \(\,\mathrm{△ADE}\,\)で相似比は\(\,4：1\,\)なので、
面積比が\(\,16：1\,\)になることから
\(\displaystyle \,\mathrm{△ADE}=\color{blue}{\frac{1}{16}}\,\)
よって、\(\,\mathrm{△FBC}\,\)は\(\,\mathrm{△ADE}\,\)の
\(\hspace{10pt}\displaystyle \color{red}{\frac{2}{5}}\div \color{blue}{\frac{1}{16}}\\
\displaystyle =\frac{2}{5}\times \frac{16}{1}\\
\displaystyle =\underline{ \frac{32}{5} } (倍)\)
次で最後です。
(3)
条件です。
\(\,\mathrm{△ABC}\,\)は正三角形
\(\,\mathrm{BD:DC=1:2}\,\)
\(\,\mathrm{AB=6}\,\)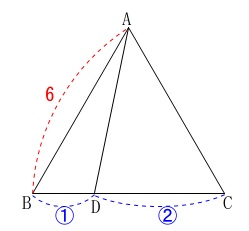
正三角形なので長さや面積は出しやすいので早速問題に入ります。
①
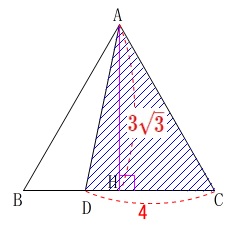
\(\,\mathrm{A}\,\)から\(\,\mathrm{BC}\,\)に垂線を引き、
\(\,\mathrm{BC}\,\)との交点を\(\,\mathrm{H}\,\)とします。
\(\,\mathrm{△ABC}\,\)は正三角形なので\(\,\mathrm{AH}\,\)は中線で長さが
\(\mathrm{AH}=\color{red}{3\sqrt{3}}\)
また、\(\,\mathrm{BD:DC=1:2}\,\)なので、
\(\mathrm{BD}=2\,,\,\mathrm{DH}=1\,,\,\mathrm{HC}=3\)
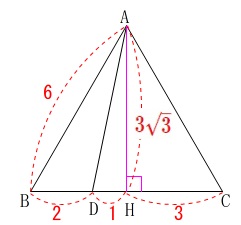三平方の定理から、
\(\begin{eqnarray}
\mathrm{AD^2}&=&\mathrm{AH^2+DH^2}\\
&=&(3\sqrt{3})^2+1^2\\
&=&28\\
\mathrm{AD}&=&\underline{ 2\sqrt{7} } (\,\mathrm{AD}\,＞\,0\,)
\end{eqnarray}\)
②
\(\,\mathrm{AD}\,\)を折り目として\(\,\mathrm{△ABD}\,\)を\(\,\mathrm{△ADC}\,\)に垂直になるように立てます。
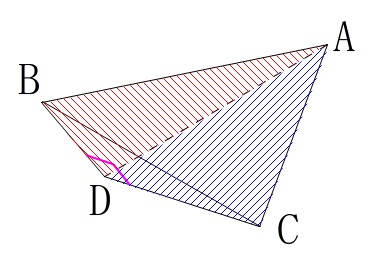見取り図を書いてもわかりにくいと思うので、簡単に説明すると、
底面が\(\,\mathrm{△ADC}\,\)
\(\,\mathrm{B}\,\)から\(\,\mathrm{△ADC}\,\)に下ろした垂線の長さ\(\,\mathrm{BI}\,\)が高さ
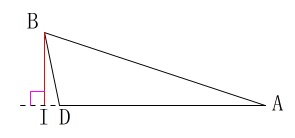この三角錐の体積を求めます。
底面\(\,\mathrm{△ADC}\,\)の面積は
\(\begin{eqnarray}\displaystyle
\mathrm{△ADC}&=&\frac{1}{2}\times \mathrm{DC}\times \mathrm{AH}\\
&=&\frac{1}{2}\times 4\times 3\sqrt{3}\\
&=&\color{blue}{6\sqrt{3}}
\end{eqnarray}\)
高さ\(\,\mathrm{BI}\,\)は\(\,\mathrm{△ABC}\,\)の面積を利用して求めます。
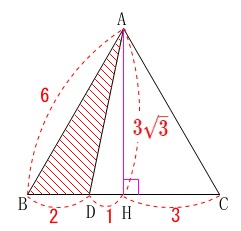
\(\begin{eqnarray}\displaystyle
\mathrm{\color{red}{△ABD}}&=&\frac{1}{2}\times \mathrm{BD}\times \mathrm{AH}\\
&=&\frac{1}{2}\times 2\times 3\sqrt{3}\\
&=&\color{red}{3\sqrt{3}}
\end{eqnarray}\)
この三角形の底辺を\(\,\mathrm{AD}\,\)と見ると高さは\(\,\mathrm{BI}\,\)になるので、
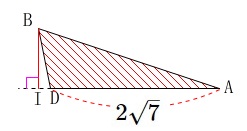
\(\begin{eqnarray}
\mathrm{\color{red}{△ABD}}&=&\frac{1}{2}\times \mathrm{AD}\times \mathrm{BI}\\
\color{red}{3\sqrt{3}}&=&\frac{1}{2}\times 2\sqrt{7}\times \mathrm{BI}\\
\mathrm{\color{magenta}{BI}}&=&\color{magenta}{\frac{3\sqrt{3}}{\sqrt{7}}}
\end{eqnarray}\)
よって、求める立体\(\,\mathrm{B-ADC}\,\)の体積\(\,\mathrm{V}\,\)は
\(\begin{eqnarray}
\mathrm{V}&=&\frac{1}{3}\times \mathrm{\color{blue}{△ADC}}\times \mathrm{\color{magenta}{BI}}\\
&=&\frac{1}{3}\times \color{blue}{6\sqrt{3}}\times \color{magenta}{\frac{3\sqrt{3}}{\sqrt{7}}}\\
&=&\underline{ \frac{18\sqrt{7}}{7} }
\end{eqnarray}\)
（問題はこれで終わりです。）
説明が足りていなくて申し訳ないですが、
実際は自分で計算して、書き出して、つなぎ合わせる必要があります。
そのため、数学の勉強のやり方次第で\(\,20\,\)分以内で終わる問題ですよ、ということを書いてみました。
何故か？
もちろん当会の教材をおすすめするためですよ。笑
試験時間余らせて満点とる必要がなければ、
教科書をしっかり理解して基本を抑えておけば合格点は取れます。
しかし、\(\,15\,\)分程度で見直しに入り、満点とって数学で差をつけたければ専念すべき教材です。
\(\,\mathrm{A}\,\)日程の解説は基本通り教科書の範囲内でしています。
⇒ 2018(平成30)年度愛知県公立高校入試B問題 数学の解説
\(\,2018\,\)年度の問題は基本だけで説明しています。
こちらの解き方が普通ですが、満点は十分に狙えますよ。
クラブ活動で忙しい！
塾に通っているのに数学が苦手！
数学の勉強時間を減らしたい！
数学の勉強方法が分からない！
その悩み、『覚え太郎』が解決します！！！
