中学1年の空間図形問題の考え方や克服ポイントと覚えておく公式

中学１年の空間図形で必要な性質と問題の考え方や苦手克服ポイント、
覚えておかなければならない基本的な公式をお伝えしておきます。
空間図形の用語を学ぶのは大学入試まで中学１年のここだけだということを知っておいて下さい。
つまり、中学１年で習って、その知識を大学入試まで持ち続けなければならないということです。
『空間図形』は『平面図形』よりもっと苦手な人が多いですが、理由ははっきりしています。
空間図形を空間図形として解こうとしているからです。

空間図形を立体で考えるのは当たりまえ？

空間図形の問題を空間で考えるのは当たり前ですか？
立体的なものだから空間で考えるのは悪いことではありません。

しかし、受験の数学問題を解く上ではそうとも言い切れません。
少なくとも私や数学の才能が無いと考えている人たちにとって、
立体を立体のまま理解出来る人は少ないのではないでしょうか。

空間認知能力がすごい人は立体を立体のまま考えていけるのかもしれませんが、
空間は超苦手という人にとっては難しいことですし、
苦手にしている原因でもあるのです。

空間図形問題へ取り組むときのポイント

どうすれば空間図形が得意とまではいえなくても、
ある程度は問題が解けるようになるかというと、
学校の先生のように優秀な方は立体のままで分かるから言ってくれないのかもしれませんが、
空間から抜き出した平面で考えるのです。

立体は平面の組み合わせでできていると考えると割とできるようになります。
慣れてくればある程度は立体のままでも考えられるようになりますから訓練次第とも言えるかもしれませんが、
平面で考えることで全て解決出来ます。

もちろん平面図形の知識は十分に習得しておかなければ意味がなく、
どうやって考えようが同じことです。

入試では2，3年で学習する合同や相似や三平方の定理が入り乱れての問題になります。
それは入試前に練習するしかありません。

しかし、1年でしかやらないこともあります。
用語と意味はしっかり覚えておきましょう。

『空間図形』での覚えておかなければならない用語をいくつか上げておきます。

中学1年での空間図形での用語ポイント

１つ目は、空間における『交わり』です。
立体交差している直線や線分の関係は何なのか、平面と直線の位置関係など、しっかり用語を理解して覚えておきましょう。
特に「ねじれの位置」には要注意です。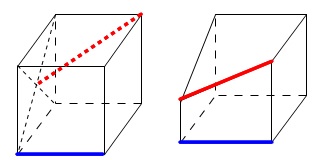立方体にある線分で見ると平行でもなく、交わりもないのでねじれに見えますが、
ねじれの位置にあるとは、「直線」で考えなくてはなりません。
図の赤線と青線は延長すると交わりますのでねじれではありません。

同一平面上にあるものは「ねじれの位置」にあるのではないのです。
しっかり理解しておいて下さい。

二つ目は、展開図と見取り図です。
平面から立体をイメージさせるという問題もよく出てきますから、
立体の見取り図はだいたいで良いので書き出してイメージ出来るようにいろいろなパターンを勉強しておきましょう。

立体から平面へのイメージも問題を簡単にするためにはもっと必要になります。

投影図もその1つです。

⇒　立体の見取り図と投影図と書き方と具体例の見方(中学１年空間図形)

３つ目は、面積や体積の求め方です。
学校ではあまり力を入れておりませんが、
１年で勉強する柱体や錐体の体積を求める公式はずっと（大学入試まで）使います。
忘れている人が非常に多いので、何度も復習して必ず覚えておきましょう。

　\(\,\color{red}{(柱体の体積)=(底面積)\times (高さ)}\,\)

　\(\,\displaystyle \color{red}{(錐体の体積)=\frac{1}{3}\times (底面積)\times (高さ)}\,\)

つまり

　\(\,\color{blue}{\displaystyle (錐体の体積)=\frac{1}{3}\times (柱体の体積)}\,\)

です。

回転体の体積なども入試でかなりのレベルで出題されますので、
中学生にとっては裏技的な公式も多く存在します。
使える人は使って良いです。
ただ、回転体などは見取り図を書くことから始めると良いですよ。

特に球体は多くの高校入試で出されています。
しかし、球体の体積や表面積を中学生が求める方法は公式以外ありません。

覚えておかなければ使えない公式

特別に難問として出されているわけではないのですが元々あつかいにくいのが球体の融合問題です。

ある程度なれておかないと時間がかかって見直しの時間がたりなくなる人が多くなるでしょうね。
多めの練習問題に当たっておくと良いでしょう。

それ以前に、球の表面積や体積の公式を覚えていない人が多いようですが、
中学生には導くことができない公式なので、
覚えていないと使えない公式です。

　半径を　\(r\)　とすると
　\(\color{red}{球の表面積は　4\pi\,r^2}\)
　\(\color{red}{球の体積は　\displaystyle \frac{4}{3}\pi\,r^3}\)　

この公式は覚えておかなければなりません。
高校生でも導けない人はたくさんいます。

だからといって使ってはいけないかというと、
問題にはでますので使わなければなりません。

何度も何度も見て、実際に問題にあたり覚えておきましょう。

公式は導けることが大切なのではありませんよ。
公式は使えることが先です。

この単元では覚えておくと試験時間が節約できるものがいくつかありますので調べておくといいでしょう。

先にも書いておきましたが、空間図形を学ぶ機会は中学１年のここだけです。
高校入試はもちろんですが、大学入試の本試験でも普通にあつかう項目なのでここできっちり基礎をおさえておきましょう。

全てが解決するわけではありませんが、
空間図形攻略の１つは「平面を抜き出す」です。

どちらかというと中学限定ですが、

⇒　立体の見取り図と投影図と書き方と具体例の見方(中学１年空間図形)

これはおさえておきましょう。

⇒　中学1年の平面図形のポイントと空間図形とのつながり

もちろん、平面図形の知識は欠かせません。
空間図形は平面図形を組合わせて（重ねて）できているのですよ。