2019年度群馬県公立高校の入試前期数学の問題と解説【後半】

2019年（平成31年）度に行われた群馬県公立高校入試（前期）の数学の問題と解説後半です。
後半は第3問が文字式と確率と円周角、第4問が1次関数の文章問題、第5問は相似と面積比の問題になります。
どれも難しい問題はなく、試験時間40分は十分足ります。

問題は群馬県が公開してくれています。

⇒　2019年（平成31年）度群馬県前期数学の問題

文字式と確率と円周角

\(\,　3　\,\)は\(\,3\,\)問あります。

(1)
正方形の1辺を\(\,a\,\mathrm{cm}\,\)長くして増える面積を文字式で表します。

※
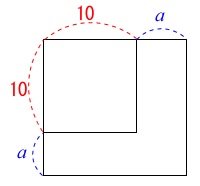
単位は\(\,\mathrm{cm}\,\)ですが途中の計算では省略します。

もとの正方形の\(\,1\,\)辺は\(\,10\,\)なので面積は
　\(\hspace{10pt}10^2=\color{red}{100}\)

\(\,1\,\)辺を\(\,a\,\)長くした正方形の面積は、
　\(\hspace{10pt}(10+a)^2=\color{blue}{a^2+20a+100}\)　

よって、増える面積は
　\(\hspace{10pt} (\color{blue}{a^2+20a+100})-(\color{red}{100})\\
=\underline{　a^2+20a　}　(\mathrm{cm^2})\)

図で見ると\(\,\color{magenta}{10\,a}\,\)の部分が2つあることが分かります。
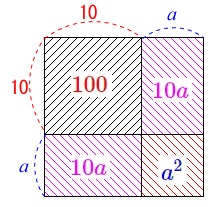「正方形」などの図形を表した日本語を見たら図を書くことです。

図形が苦手という人程、図をあまり書かないですね。
当会ではそれを「解く気がない。」といいます。
（会員意外には言いませんけど。言ってるかな？笑）

(2)
整数と確率です。
樹形図で終わりますが、約数を見ていけばすぐに答えは求まります。

さいころを\(\,2\,\)回投げるので、目の出方は\(\,36\,\)通りあります。
その出目の和を\(\,a\,\)とするとき、
　出る目の和が最も小さいのは\(\,1\,\)回目\(\,2\,\)回目ともに\(\,1\,\)のときで\(\,\color{blue}{2}\,\)
　出る目の和が最も大きいのは\(\,1\,\)回目\(\,2\,\)回目ともに\(\,6\,\)のときで\(\,\color{red}{12}\,\)
だから
　\(\color{blue}{2}\,≦\,a\,≦\,\color{red}{12}\)
なので、
　\(\,ax=24\,\)を満たす整数\(\,a,x\,\)は\(\,24\,\)の約数
ただし、\(\,a\,\)が\(\,2\,≦\,a\,≦\,12\,\)の範囲なので、
　\(\,a\,\)は\(\,24\,\)の約数のうち\(\,1,24\,\)以外の数
になります。

この\(\,a\,\)を1つ決めると、対応する\(\,x\,\)は1つ整数で存在するので、
さいころを\(\,2\,\)回投げて、その和を\(\,a\,\)とするとき、
\(\,a\,\)が\(\,2,3,4,6,8,12\,\)となる確率を求めることと同じです。

出る目の和が\(\,2,3,4,6,8,12\,\)となるのは、

　\(\begin{array}{|c|c|c|c|c|c|c|} \hline
& \color{red}{1} & \color{red}{2} & \color{red}{3} & \color{red}{4} & \color{red}{5} & \color{red}{6}\\ \hline
\,\color{blue}{1}\, & ○ & ○ & ○ & & ○ & \\ \hline
\color{blue}{2} & ○ & ○ & & ○ & & ○\\ \hline
\color{blue}{3} & ○ & & ○ & & ○ & \\ \hline
\color{blue}{4} & & ○ & & ○ & & \\ \hline
\color{blue}{5} & ○ & & ○ & & & \\ \hline
\color{blue}{6} & & ○ & & & & ○\\ \hline
\end{array}\)

の\(\,17\,\)通りなので求める確率は
　\(\displaystyle \underline{　\frac{17}{36}　}\)

\(\,x\,\)についての方程式ですが\(\,x\,\)を求める必要はありません。

地道に、
　\(\,a\,\)が\(\,2\,\)のとき、\(\,x\,\)は整数解が存在する。
このとき\(\,a=2\,\)となるのは\(\,1\,\)通り。
　\(\,a\,\)が\(\,3\,\)のとき、\(\,x\,\)は整数解が存在する。
このとき\(\,a=3\,\)となるのは\(\,2\,\)通り。
・・・
と順にすべて調べていっても\(\,a,x\,\)は自然数なので限られています。
整数が関係する問題によく使う方法ですね。

(3)
角度を求める問題は分かる角度を順に書き込んで行けば答えは出ます。
　線分\(\,\mathrm{BD}\,\)が直径であることから、
　\(\,\mathrm{∠BCD=\color{red}{90^{\circ}}}\,\)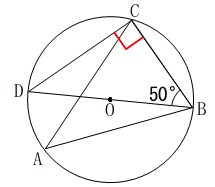　\(\,\mathrm{△BCD}\,\)の内角の和が180°であることから、
　\(\,\mathrm{∠BDC=\color{blue}{40^{\circ}}}\,\)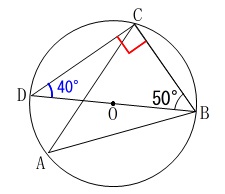　同一の弧に対する円周角は等しいから、
　\(\,\mathrm{∠ACB}=\color{blue}{40°}\,\)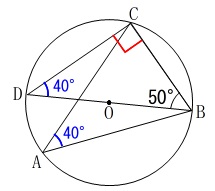　条件の\(\,\mathrm{AB=AC}\,\)から\(\,\mathrm{△ABC}\,\)は二等辺三角形だから底角が等しくなるので
　\(\begin{eqnarray}\displaystyle
\mathrm{∠ABC}&=&\mathrm{∠ACB}\\
&=&\frac{180^{\circ}-40^{\circ}}{2}\\
&=&\color{magenta}{70^{\circ}}
\end{eqnarray}\)　よって、
　\(\begin{eqnarray}
\mathrm{∠ACD}&=&90^{\circ}-70^{\circ}\\
&=&\underline{　20^{\circ}　}
\end{eqnarray}\)

求めたい角度がすぐに出なくても分かる角度だけでも書き込んでみる、
それをするか、しないか、その違いは大きいです。

1次関数の文章問題

\(\,　4　\,\)

文章題に見えますね。笑
単なる\(\,1\,\)次関数の問題です。

ガス料金を求める計算式が与えられています。
ここでは\(\,\mathrm{1\,m^3}\,\)当たりにかかる料金を「単価」と呼ぶことにします。
※
単位は\(\,円と\,\mathrm{m^3}\,\)ですが途中の計算では省略します。

　\(\,\color{blue}{(ガス料金)=(基本料金)+(単価)\times (使用量)}\,\)

(1)
ガス会社\(\,\mathrm{A}\,\)だけの料金なので、
ガス会社\(\,\mathrm{B}\,\)のことは考えなくて良いです。

計算式を見てもわかるように、
　使用量を\(\,x\,\)　料金を\(\,y\,\)
とすると
　単価が傾き\(\,\color{red}{a}\,\)、基本料金が\(\,y\,\)切片\(\,\color{blue}{b}\,\)
の\(\,1\,\)次関数になります。
　\(y=\color{red}{a}\,x+\color{blue}{b}\)

使用量\(\,x\,\)が\(\,2.2\,\)のとき、料金\(\,y\,\)は\(\,2822\,\)
使用量\(\,x\,\)が\(\,3.1\,\)のとき、料金\(\,y\,\)は\(\,3281\,\)です。

これを連立すると、

　　\( \begin{cases}
\hspace{7pt} 2822=2.2\,\color{red}{a}+\color{blue}{b}　･･･①\\ \\
\hspace{7pt} 3281=3.1\,\color{red}{a}+\color{blue}{b}　･･･②
\end{cases}\)

これを解くと、②-①から
　\(\begin{eqnarray}
0.9\,\color{red}{a}&=&459\\
9\,\color{red}{a}&=&4590\\
\color{red}{a}&=&510
\end{eqnarray}\)

①にもどすと（②でも良いですよ。）
　\(\begin{eqnarray}
2822&=&2.2\times 510+\color{blue}{b}\\
&=&1122+\color{blue}{b}\\
\color{blue}{b}&=&1700
\end{eqnarray}\)

答え　基本料金　\(\,\underline{　1700　}\,(円)\,\)　単価　\(\,\underline{　510　}\,(円)\,\)

１次関数の傾きと切片を求める基本問題でした。

(2)
今度はガス会社\(\,\mathrm{B}\,\)も出てきますが、使用量が同じなので料金の比較ができます。

ガス会社の基本料金は\(\,\mathrm{A}\,\)より\(\,\mathrm{B}\,\)は\(\,90\,\)円安いので\(\,\color{blue}{1610}\,\)円です。
これは(1)ができていないと求まらない問題ですね。

ガス会社\(\,\mathrm{B}\,\)の単価を\(\,\color{red}{c}\,\)とすると\(\,\mathrm{B}\,\)のガス料金\(\,y\,\)は、
　\(y=\color{red}{c}\,x+\color{blue}{1610}\)

使用量が\(\,4.5\,\mathrm{m^3}\,\)のとき、
\(\,\mathrm{B}\,\)の料金は
　\(y=4.5\,\color{red}{c}+\color{blue}{1610}\)
\(\,\mathrm{A}\,\)の料金は(1)から
　\(\begin{eqnarray}
y&=&510\times 4.5+1700\\
&=&3995
\end{eqnarray}\)

使用量が\(\,4.5\,\mathrm{m^3}\,\)のとき、\(\,\mathrm{A}\,\)と\(\,\mathrm{B}\,\)の料金が同じになるので、
　\(\begin{eqnarray}
3995&=&4.5\,\color{red}{c}+1610\\
39950&=&45\,\color{red}{c}+16100\\
45\,\color{red}{c}&=&23850\\
\color{red}{c}&=&\underline{　530　}　(円)
\end{eqnarray}\)

グラフは書かなくて良いでしょう。
傾きと切片の違う\(\,2\,\)本の直線が、
　交わる点が同じ使用量で同じ料金
ですので、自分で確認してみて下さい。

平行四辺形の性質と相似と面積比

\(\,　5　\,\)
平行四辺形で角度が与えられていないので長方形でも面積比は同じですが、
平行四辺形のまま進めます。

(1)
相似の証明です。
これは長さがなくても成り立ちます。

平行四辺形の性質から錯角が等しくなります。
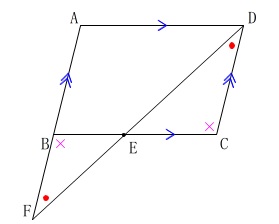　\(\,2\,\)組の角がそれぞれ等しくなるので
　\(\,\mathrm{△BFE}\,\)　∽　\(\,\mathrm{△CDE}\,\)

もちろん対頂角も等しいので、1つの錯角と対頂角が等しいことからでも良いです。

証明は自分で書いておいて下さい。

(2)
長さを書き込むと相似比がすぐに分かります。
　\(\,\mathrm{AD=7　,　BE=\color{red}{3}}\,\)
なので\(\,\mathrm{EC=\color{blue}{4}}\,\)です。
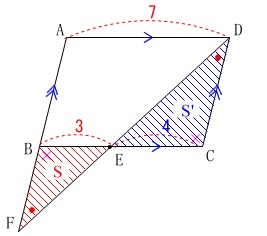　\(\,\mathrm{△BFE}\,\)　∽　\(\,\mathrm{△CDE}\,\)　で相似比が\(\,\color{red}{3}:\color{blue}{4}\,\)なので、
面積比は
　\(\begin{eqnarray}
\mathrm{S:S’}&=&\color{red}{3}^2:\color{blue}{4}^2\\
&=&\underline{　9:16　}
\end{eqnarray}\)

相似比が\(\,a:b\,\)のとき面積比は\(\,\color{red}{a^2:b^2}\,\)ですよ。

(3)
今度は△\(\,\mathrm{BFE}\,\)と平行四辺形\(\,\mathrm{ABCD}\,\)の面積比です。
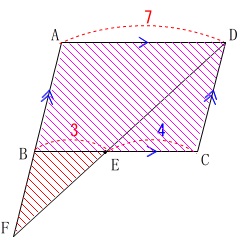辺\(\,\mathrm{AB}\,\)に平行な線分\(\,\mathrm{EG}\,\)を引くと、
　\(\,\mathrm{△CDE=△GED}\,\)　（面積が等しい）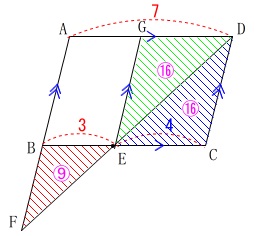
このとき四角形\(\,\mathrm{ABEG}\,\)と四角形\(\,\mathrm{GECD}\,\)の面積比は\(\,\color{red}{3}:\color{red}{4}\,\)になるので、
\(\,\mathrm{△CDE}=\color{magenta}{16}\,\)と表すと
　\(\begin{eqnarray}
\mathrm{ABEG:GECD}&=&\color{red}{3}:\color{blue}{4}\\
\mathrm{ABEG}:(\color{magenta}{16}+\color{magenta}{16})&=&\color{red}{3}:\color{blue}{4}\\
\mathrm{ABEG}:\color{magenta}{32}&=&\color{red}{3}:\color{blue}{4}\\
\color{blue}{4}\times \mathrm{ABEG}&=&\color{red}{3}\times \color{magenta}{32}\\
\mathrm{ABEG}&=&\color{blue}{24}
\end{eqnarray}\)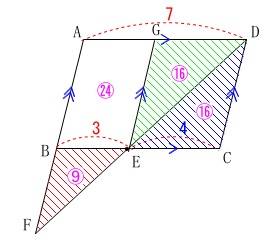
よって\(\,\mathrm{△BFE}\,\)の面積\(\,\mathrm{S}\,\)と平行四辺形\(\,\mathrm{ABCD}\,\)の面積\(\,\mathrm{T}\,\)との比は
　\(\begin{eqnarray}
\mathrm{S:T}&=&9:(\color{magenta}{32}+\color{blue}{24})\\
&=&\underline{　9:56　}
\end{eqnarray}\)

あれ？\(\,\mathrm{AB=5}\,\)を使ってませんね。
\(\,\mathrm{△BFE}\,\)　∽　\(\,\mathrm{△AFD}\,\)を使う所だったのかもしれません。
相似比が\(\,3:7\,\)なので面積比が\(\,9:49\,\)だから
　\(\,\mathrm{△BFE}:(台形\mathrm{ABED})=9:40\,\)
よって、
　\(\begin{eqnarray}
\mathrm{S:T}&=&9:(16+40)\\
&=&\underline{　9:56　}
\end{eqnarray}\)
同じ結果が出てきます。