2019年（平成30年)度に群馬県で行われた公立高校入試の前期選抜数学の問題と解答解説です。
試験時間は40分ですが十分な時間ですので、満点目指して基本の復習を徹底しておきましょう。
2019年の前期選抜数学の平均点は50点満点中28.8点でした。
問題は群馬県で公開してくれています。
前期数学問題 ⇒ 2019年群馬県前期選抜数学の問題
数と文字式の計算を中心とした小問集合
\(\, 1 \,\)は配点が全体の\(\,3\,\)割ちょっとある計算問題です。
計算ミスは大きな失点になりますので確実に得点しておきましょう。
正負の数と文字式と無理数の計算
(1)①から⑥までの計算問題です。
①
正の数と負の数の和です。
\(\hspace{10pt}-7+3\\
=\underline{ -4 }\)
ここではきれいな整数値の計算なので説明する必要はないとは思いますが、
正の数負の数の加減（足し算引き算）は数直線で見ると簡単ですよ。
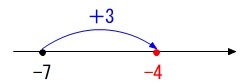無理数の場合でも同じようにすると数直線上で確認できます。
②
同じ文字（同類項）の引き算は係数の引き算です。
\(\hspace{10pt}5x-2x\\
=\underline{ 3x }\)
③
分数の文字式の計算です。
分子には（かっこ）が付いていることを忘れないようにしましょう。
\(\hspace{10pt}\displaystyle 8\times \frac{3a-1}{4}\\
\displaystyle =\frac{\color{red}{8}(3a-1)}{\color{red}{4}}\\
\displaystyle =\color{red}{2}(3a-1)\\
=\underline{ 6a-2 }\)
言うまでもありませんが、約分が先です。
④
文字式の展開です。
展開して同類項をまとめます。
\(\hspace{10pt} 4x+5y-(x+3y)\\
=4x+5y-x-3y\\
=\underline{ 3x+2y }\)
計算過程で\(\,2\,\)行目の（かっこ）を外したときの\(\,1\,\)行は省略しない方が良いです。
たいして時間は変わりませんが、計算ミスは確実に減りますよ。
⑤
文字式の割り算です。
割り算は逆数のかけ算です。
\(\hspace{10pt} 4\,a^3\,b\div 2\,a\,b\\
\displaystyle =\frac{4\,a^3\,b}{2\,a\,b}\\
=\underline{ 2\,a^2 }\)
約分しなくても計算できる問題ですが、
分数計算は約分を利用すれば分母が残るややこしい計算でも同じです。
⑥
無理数の引き算です。
ルートの中身が同じときだけ係数の引き算ができます。
\(\hspace{10pt}\sqrt{50}-\sqrt{8}\\
=5\sqrt{2}-2\sqrt{2}\\
=\underline{ 3\sqrt{2} }\)
「計算ミスはしない」という人はこの解説は見ていないでしょうから言っておきますが、
ルートの中身を簡単にするとき、素因数分解は確実にした方が良いですよ。
文字式の展開と因数分解
(2)文字式の展開です。
暗算できる展開ですが、ここは一つひとつ展開した方が良いです。
\(\hspace{10pt}(x+3)(2x-1)\\
=2x^2-x+6x-3\\
=\underline{ 2x^2+5x-3 }\)
展開公式
\((ax+b)(cx+d)=acx^2+(ad+bc)x+bd ･･･①\)
は覚えなくて良いです。
⇒ 文字式の展開公式で覚えなくて良い公式と覚えた方が良い公式(中学3年)
何度も練習しているうちに展開は暗算できるようにはなりますが、
上の公式①は高校に進学しても使いません。笑
因数分解や別の方法で利用することがあるので覚えても良いですが、
中学生は係数が文字のまま覚える必要はありません。
(3)
因数分解は手順が決まっています。
この問題は公式利用だけで終わります。
\(\hspace{10pt}x^2-9y^2\\
=(x)^2-(3y)^2\\
=(x+3y)(x-3y)\)
因数分解公式
\(\color{red}{a^2-b^2=(a+b)(a-b)}\)
を利用しました。
因数分解は公式が少ないので必ず覚えておきましょう。
ここまでで\(\,50\,\)点満点中\(\,16\,\)点が配点されています。
方程式、体積、関数、データの小問題
\(\, 2 \,\)も小問集合です。
基本の確認問題ばかりですのでここも確実に得点しておきましょう。
等式の作成と四面体の体積
(1)
数量関係を等式にします。
\(\,1\,\)個\(\,\color{red}{a}\,\mathrm{g}\,\)のおもり\(\,\color{red}{2}\,\)個
\(\,1\,\)個\(\,\color{blue}{b}\,\mathrm{g}\,\)のおもり\(\,\color{blue}{3}\,\)個
合わせると合計\(\,\color{magenta}{500}\,\mathrm{g}\,\)になる。
\(\hspace{10pt}\color{red}{a}\times \color{red}{2}+\color{blue}{b}\times \color{blue}{3}=\color{magenta}{500}\\
\underline{ 2a+3b=500 }\)
日本語で書かれた関係を数学の記号を使って等式にするだけです。
(2)
四面体\(\,\mathrm{ABCF}\,\)の体積ですが三角錐（すい）です。
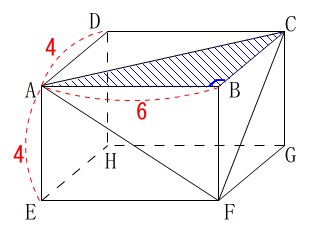底面の三角形は好きな面を選んで良いですよ。
ここでは\(\,\mathrm{△ABC}\,\)を底面として見ます。
底面を\(\,\mathrm{△ABC}\,\)、高さを\(\,\mathrm{BF}\,\)と見ると、
\(\begin{eqnarray}\displaystyle
\mathrm{△ABC}&=&\frac{1}{2}\times 6\times 4\\
&=&12
\end{eqnarray}\)
なので四面体\(\,\mathrm{ABCF}\,\)の体積を\(\,\mathrm{V}\,\)とすると、
\(\begin{eqnarray}\displaystyle
\mathrm{V}&=&\frac{1}{3}\times \mathrm{△ABC}\times \mathrm{BF}\\
&=&\frac{1}{3}\times 12\times 4\\
&=&\underline{ 16 } (\mathrm{cm^3})
\end{eqnarray}\)
錐体なので\(\displaystyle \frac{1}{3}\)をかけ忘れないようにしましょう。
求める四面体\(\,\mathrm{ABCF}\,\)の体積\(\,\mathrm{V}\,\)は直方体の半分（三角柱）の\(\displaystyle \frac{1}{3}\)です。
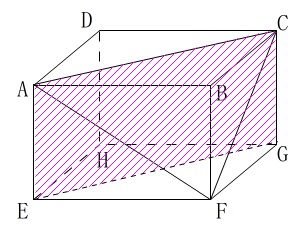直方体の体積は
\(\hspace{10pt}\color{red}{6}\times \color{red}{4}\times \color{red}{4}=\color{blue}{96}\)
（これは後で約分するので計算しなくて良いです。）
なので
\(\begin{eqnarray}
\mathrm{V}&=&\color{blue}{96}\times \frac{1}{2}\times \frac{1}{3}\\
&=&\underline{ 16 } (\mathrm{cm^3})
\end{eqnarray}\)
どちらでも良いですよ。
２次方程式と関数の変域
(3)
\(\,2\,\)次方程式を解の公式を利用して解きます。
⇒ ２次方程式の解の公式の二通りの求め方と文章題の解き方(中学３年)
方程式を解くときの基本は左辺にすべての項を集めて右辺を\(\,0\,\)にすることです。
\(\begin{eqnarray}
(x-1)^2&=&x+4\\
x^2-2x+1&=&x+4\\
x^2-2x+1-x-4&=&0\\
x^2-3x-3&=&0
\end{eqnarray}\)
左辺は因数分解できないので解の公式ですね。
\(\begin{eqnarray}\displaystyle
x&=&\frac{-(-3)\pm \sqrt{(-3)^2-4\times 1\times (-3)}}{2\times 1}\\
&=&\frac{3\pm \sqrt{9+12}}{2}\\
&=&\underline{ \frac{3\pm \sqrt{21}}{2} }
\end{eqnarray}\)
2次方程式を解くときは因数分解を利用するか解の公式を利用するかなので、
因数分解できないときはあれこれ変形を考えるより、
解の公式を利用して確実に処理した方がはやい場合が多いです。
(4)
関数の変域問題です。
関数 \(\,y=x^2\,\)
\(\,x\,\)の変域 \(\,-1\,≦\,x\,≦\,3\,\)
\(\,x=-1\,\)のとき\(\,(\,-1\,,\,1\,)\,\)
\(\,x=3\,\)のとき\(\,(\,3\,,\,9\,)\,\)
ですが、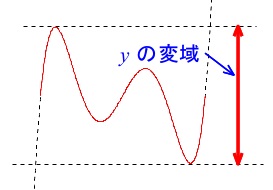
\(\,y\,\)の変域に\(\,(\,-1\,,\,1\,)\,\)は関係ありません。
答え \(\,\underline{ 0\,≦\,y\,≦\,9 }\,\)
変域から数値だけを見るより、
簡単なグラフを書いて考えた方が早くて確実です。
データの活用（代表値とヒストグラム）
(5)
代表値が与えられている正しいヒストグラムを探します。
平均値を計算したいところですが、階級値に度数をかけて、という計算を繰り返すのは時間がかかります。
中央値と最頻値から間違っているものを消していきましょう。
\(\,20\,\)人のデータだから、
小さい順に\(\,10\,\)人目と\(\,11\,\)人目がいる階級の階級値が中央値です。
中央値は、
ア：\(\,7\,\)点 イ：\(\,6\,\)点 ウ：\(\,7\,\)点 エ：\(\,6\,\)点
中央値は\(\,\color{red}{7}\,\)点なので\(\,イ\,\)と\(\,エ\,\)は違います。
最頻値は度数が一番多い階級の階級値なので、
ア：\(\,7\,\)点 ウ：\(\,7\,\)点
2つとも最頻値は\(\,\color{blue}{7}\,\)点で一致しています。
最頻値は問題になくても良いですが、最頻値から見れば、\(\,エ\,\)がすぐに除外できます。
平均値は\(\,\color{magenta}{6.3}\,\)点です。
アとウの平均値は、階級値と度数をかけて合計して\(\,20\,\)で割れば出てきますが、
アのヒストグラムは\(\,7\,\)点を軸に左右対称になっているので平均点は\(\,7\,\)点なので違っています。
残ったのは\(\,\color{red}{ウ}\,\)です。
ウの平均値を確認しておきます。
\(\hspace{10pt}\displaystyle \frac{3\times 2+4\times 2+5\times 2+6\times 3+7\times 6+8\times 3+9\times 2}{20}\\
\displaystyle =\frac{6+8+10+18+42+24+18}{20}\\
\displaystyle =\frac{126}{20}\\
=6.3\)
平均値\(\,\color{magenta}{6.3}\,\)に一致しました。
答え \(\,\underline{ ウ }\,\)
平均値からすべて見るとかなり時間が必要になりますよ。
ここまでで配点の半分以上なのでここで区切ります。
⇒ 2019年度群馬県公立高校の入試前期数学の問題と解説【後半】
後半は、
\(\,3\,\)が文字式、確率、角度
\(\,4\,\)が1次関数の文章題
\(\,5\,\)が平行四辺形の性質と面積比
となっています。
前期は選抜試験が早い時期に行われるので中学最後の方の単元内容が薄い分簡単にはなりますが、
前期後期ともに例年出題分野に偏りが少ない問題構成です。
クラブ活動で忙しい！
塾に通っているのに数学が苦手！
数学の勉強時間を減らしたい！
数学の勉強方法が分からない！
その悩み、『覚え太郎』が解決します！！！
