2019年群馬県公立高校後期入試の数学の問題と解説

2019年（平成31年）度に群馬県で行われた公立高校後期選抜入試の数学の問題と解説です。
全体で20問程度ありますが手を動かせばそれほど応用が必要な問題はありません。
数値はきれいで計算力もそれほど必要とはしません。
試験時間は45分から60分で学校ごとに指定されますが45分は満点とるには十分な時間です。

問題は群馬県が公開してくれています。

⇒　2019年度群馬県立高校入試後期数学の問題

大問で\(\,　1　\,\)から\(\,　6　\,\)まであります。

１．計算中心の基本問題小問集合

式の計算と無理数の性質

(1)
式の計算です。

①
符号を忘れないようにしましょう。
　\(\hspace{10pt}-4\times 3\\
=\underline{　-12　}\)

②
約分しますが分母と分子をはっきり区別すれば問題ありません。

　\(\hspace{10pt}\displaystyle 6\,a^2\times \frac{1}{2}\,a\\
\displaystyle =\frac{6\,a^2\times a}{\color{red}{2}}\\
=\underline{　3\,a^3　}\)

分母にくるのは\(\,\color{red}{2}\,\)だけです。

③
同類項をまとめます。

　\(\hspace{10pt}\displaystyle \frac{x+y}{2}+\frac{x-y}{4}\\
\displaystyle =\frac{2(x+y)+(x-y)}{4}\\
\displaystyle =\frac{2x+2y+x-y}{4}\\
\displaystyle =\underline{　\frac{3x+y}{4}　}\)

分母を1つにして、分子の計算に集中すると分数計算はミスしにくいですよ。
分子には（かっこ）が付いていることを忘れないようにして下さい。

(2)
ルートの付いた無理数の大小はルートの中身の大小になります。
　\(\hspace{10pt}\color{blue}{2}\,＜\,\sqrt{a}\,＜\,\color{red}{3}\\
\color{blue}{\sqrt{4}}\,＜\,\sqrt{a}\,＜\,\color{red}{\sqrt{9}}\)
よって、これを満たす自然数\(\,a\,\)は
　\(a=\underline{　5\,,\,6\,,\,7\,,\,8　}\)

正の数は平方しても大小関係は変わらないので、
　\(\hspace{10pt}\color{blue}{2}\,＜\,\sqrt{a}\,＜\,\color{red}{3}\\
\hspace{10pt}\color{blue}{4}\,＜\hspace{5pt}a\hspace{4pt}\,＜\,\color{red}{9}\)
としても良いですよ。

因数分解と代入計算と２次方程式の解

(3)
定数項に着目します。
かけて定数項の\(\,-6\,\)になる整数の組み合わせは
　\(\color{black}{\fbox{1×( – 6 )}}\)　　\(\color{black}{\fbox{2×( – 3 )}}\)　
　\(\color{black}{\fbox{( – 1 )×6}}\)　　\(\color{black}{\fbox{( – 2 )×3}}\)
この中で、2つの因数を足して\(\,x\,\)の\(\,1\,\)次の係数\(\,+5\,\)になるのは
　\((-1)\times 6\)
なので
　\(\hspace{10pt}x^2+5x-6\\
=\underline{　(x-1)(x+6)　}\)

(4)
代入するのは与式（求値式）を簡単にしてからです。

　\(\hspace{10pt}(-a\,b)^3\div a\,b^2\\
\displaystyle =-\frac{a^3\,b^3}{a\,b^2}\\
=-a^2\,b\\
=-(3)^2\times (-4)\\
=\underline{　36　}\)

代入するときは正の数であろうが負の数であろうが（かっこ）を付けておくとミスは減ります。

(5)
\(\,2\,\)次方程式に限らず方程式では左辺にすべての項を集めて右辺を\(\,0\,\)にするのが基本です。

　\(\begin{eqnarray}
x^2&=&6x\\
x^2-6x&=&0\\
x(x-6)&=&0\\
x&=&\underline{　0\,,\,6　}
\end{eqnarray}\)

共通因数として出てくる\(\,x=0\,\)を忘れないようにして下さい。

円周角の定理と確率

(6)
中心角は円周角の\(\,2\,\)倍です。
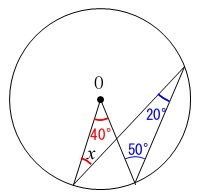円周角が\(\,\color{blue}{20°}\,\)なので中心角は\(\,\color{red}{40°}\,\)です。

三角形の内角の和が一定であることと、対頂角が等しいことから、
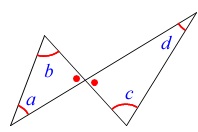図において
　\(\hspace{10pt}a+b=c+d\)
よって、
　\(\begin{eqnarray}
x+\color{red}{40^{\circ}}&=&\color{blue}{20^{\circ}}+\color{blue}{50^{\circ}}\\
x&=&70^{\circ}-\color{red}{40^{\circ}}\\
&=&\underline{　30^{\circ}　}
\end{eqnarray}\)

(7)
\(\,4\,\)枚の硬貨を\(\,\mathrm{A,B,C,D}\,\)と区別して樹形図ですぐ解決します。
ここでは表が\(\,○\,\)、裏が\(\,×\,\)として表にしておきます。
　\(\begin{array}{|c|c|c|c|c|} \hline
\,\mathrm{A}\, & \,\mathrm{B}\, & \,\mathrm{C}\, & \,\mathrm{D}\, & \\ \hline
○ & ○ & ○ & ○ & \\ \hline
○ & ○ & ○ & × & \\ \hline
○ & ○ & × & ○ & \\ \hline
○ & ○ & × & × &　\color{red}{●}　\\ \hline
○ & × & ○ & ○ & \\ \hline
○ & × & ○ & × &　\color{red}{●}　 \\ \hline
○ & × & × & ○ & 　\color{red}{●}　\\ \hline
○ & × & × & × & \\ \hline
× & ○ & ○ & ○ & \\ \hline
× & ○ & ○ & × &　\color{red}{●}　 \\ \hline
× & ○ & × & ○ &　\color{red}{●}　 \\ \hline
× & ○ & × & × & \\ \hline
× & × & ○ & ○ &　\color{red}{●}　 \\ \hline
× & × & ○ & × & \\ \hline
× & × & × & ○ & \\ \hline
× & × & × & × & \\ \hline
\end{array}\)

よって求める確率は
　\(\displaystyle \frac{6}{16}=\underline{　\frac{3}{8}　}\)
樹形図の方が早いし見やすいですね。笑

(7)
円柱の表面積を求めますが、数値だけ見ていても始まりません。
底面の半径が\(\,\color{red}{3}\,\)、高さが\(\,\color{blue}{4}\,\)の円柱です。（単位は\(\,\mathrm{cm}\,\)です。）
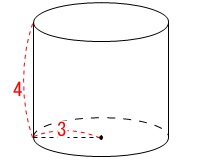求めるのは表面積なので当然展開図を書きます。
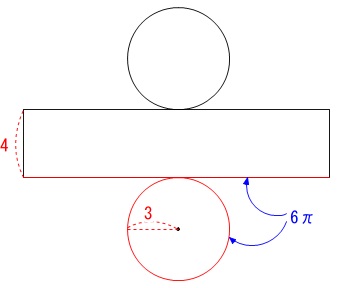底面の周の長さと側面の横の長さは等しくなるので、
側面積は
　\(\hspace{10pt}6\,\pi \times 4=\color{blue}{24\,\pi}\)
底面積は円2つ分なので、
　\(\hspace{10pt}2\times \pi\,(3)^2=\color{red}{18\,\pi}\)
求める表面積は、
　\(\hspace{10pt}\color{blue}{24\,\pi} +\color{red}{18\,\pi}\\
=\underline{　42\,\pi　(\mathrm{cm^2})}\)