2020年東京都立高校入試前期数学の関数問題の解説(第3問)

2020年（令和2年）に行われた東京都立入試前期の第3問関数問題の解説です。
第3問は関数総合問題で放物線と値域、2点を通る直線の式、四角形と三角形の面積の比が一定になるときの点を求める問題があります。
第3問の文字設定さえ迷わなければ、扱う数値はきれいな数値だけです。

\(\color{black}{\fbox{　3　}}\)の問題です。

⇒　2020円東京都立高校入試の数学第3問の問題

\(\color{black}{\fbox{　3　}}\)に共通する条件を書き出しておきます。
これは全問に対して利用する条件になります。

　曲線\(\,\ell\,\)は関数\(\displaystyle \,y=\frac{1}{4}x^2\,\)
　点\(\,\mathrm{A}\,\)は曲線\(\,\ell\,\)上の点で\(\,x\,\)座標が\(\,\color{red}{4}\,\)
　点\(\,\mathrm{P}\,\)は\(\,\ell\,\)上の点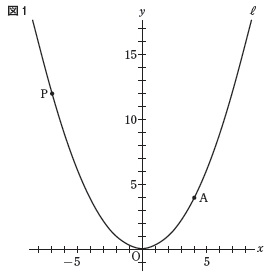

〔問１〕放物線の変域

点\(\,\mathrm{A}\,\)は\(\,\ell\,\)上の点での\(\,x\,\)座標が\(\,\color{red}{4}\,\)と分かっているので\(\,y\,\)座標も分かります。

　\(\begin{eqnarray}\displaystyle
y&=&\frac{1}{4}\times (\color{red}{4})^2\\
&=&4
\end{eqnarray}\)

なので\(\,\mathrm{\color{blue}{A\,(\,4\,,\,4\,)}}\,\)です。

問題の\(\,a\,\)と\(\,b\,\)はそれぞれ、
　\(\,a\,\)は\(\,x\,\)の変域（定義域）
　\(\,b\,\)は\(\,y\,\)の変域（値域）
を表しているだけで難しく考えてはダメです。

　\(\,-8≦a≦2\,\)なので\(\,-8≦x≦2\,\)
このとき関数\(\displaystyle \,y=\frac{1}{4}x^2\,\)の\(\,y\,\)の変域はどうなるか、が問題です。

　\(\,x=-8\,\)のとき\(\displaystyle \,y=\frac{1}{4}\times (-8)^2=16\,\)

　\(\,x=2\,\)のとき　\(\displaystyle \,y=\frac{1}{4}\times (2)^2=1\,\)

ですが\(\,y\,\)の変域は
　\(\,1≦y≦16\,\)
ではありません。
\(\,y\,\)の値は一度\(\,0\,\)まで減少して、もう一度\(\,1\,\)まで増加しています。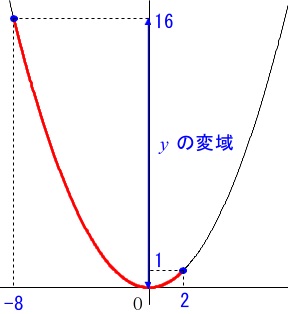
\(\,y\,\)の変域は\(\,0≦y≦16\,\)です。

つまり、
　\(\color{black}{\fbox{　0　}}\)\(\,≦b≦\,\)\(\color{black}{\fbox{　16　}}\)

答え　①　\(\,\underline{　ウ　}\,\)　②　\(\,\underline{　キ　}\,\)

\(\,y\,\)の変域（値域）は、
　\(\,x\,\)の下限（一番小さいとき）の値
と
　\(\,x\,\)の上限（一番大きいとき）の値
で決まるわけではありません。

\(\,x\,\)が動ける範囲での\(\,y\,\)の最大と最小の範囲が\(\,y\,\)の範囲（値域）です。
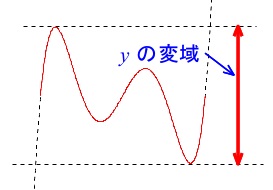すべての関数で同じなので高校になってややこしい関数（グラフ）になっても間違えないようにしましょう。

〔問２〕2点を通る直線の式の傾きと切片

点\(\,\mathrm{P}\,\)は放物線上の点なので、
　\(\,x=-6\,\)のとき\(\displaystyle \,y=\frac{1}{4}\times (-6)^2=9\,\)
だから
　\(\,\mathrm{P\,(\,-6\,,\,9\,)}\,\)
この点と
　\(\,\mathrm{A\,(\,4\,,\,4\,)}\,\)
の\(\,2\,\)点を通る直線を求めます。

求める直線を\(\,y=ax+b\,\)とおいて、連立方程式を解いても良いです。
ここでは傾きから求めます。

傾きは変化の割合と同じで
　\(\displaystyle \color{red}{(傾き)=\frac{　y\,の増加量　}{　x\,の増加量　}}\)
だから
　\(\begin{eqnarray}
傾き&=&\frac{　4-9　}{　4-(-6)　}\\
&=&\frac{-5}{10}\\
&=&-\frac{1}{2}
\end{eqnarray}\)

このとき求める直線は
　\(\displaystyle y=-\frac{1}{2}x+b\)
とおけて、これが点\(\,\mathrm{A,P}\,\)を通るのでどちらかを代入して切片\(\,b\,\)を求めます。

点\(\,\mathrm{A\,(\,4\,,\,4\,)}\,\)を代入すると、
　\(\begin{eqnarray}
4&=&-\frac{1}{2}\times (4)+b\\
&=&-2+b\\
b&=&6
\end{eqnarray}\)

よって求める直線は、
　\(\displaystyle y=\color{black}{\fbox{\(\,-\frac{1}{2}\,\)　}}x+\color{black}{\fbox{　6　}}\)

答え　③　\(\,　エ　\,\)　④　\(\,　イ　\,\)

軽く見直す程度にグラフに書き込むと計算ミスのおおよその確認ができます。
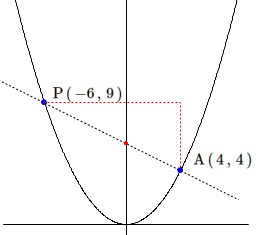傾きも切片（\(\,y\,\)切片）も出てきた数値と一致しているようです。

問題にあるグラフに\(\,2\,\)点を通る直線を書き込んで、「傾きと切片がだいたいこれくらい」ということから答えを選ぶのはやめておきましょう。
この問題では\(\,x\,\)軸方向と\(\,y\,\)軸方向の長さの比率が同じなので良いですが、わざと変えてある場合があるので気をつけておくと良いです。
　

〔問３〕四角形と三角形の面積比が4:1となる点を求める

点\(\,\mathrm{P}\,\)が放物線上の点であることは変わりません。
ただし、\(\,x\,\)座標は\(\,4\,\)より大きい値です。

点\(\,\mathrm{A(4,4)}\,\)は固定
点\(\,\mathrm{B}\,\)は\(\,y\,\)軸を対称の軸とする点\(\,\mathrm{A}\,\)の対称な点
点\(\,\mathrm{Q}\,\)は点\(\,\mathrm{P}\,\)と\(\,x\,\)座標が同じ\(\,x\,\)軸上の点
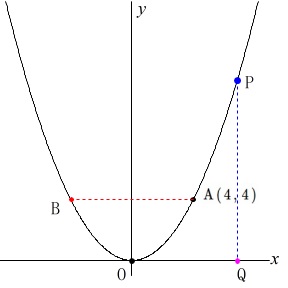このあと点と点を結ぶ説明がありますが読まなくて良いです。笑

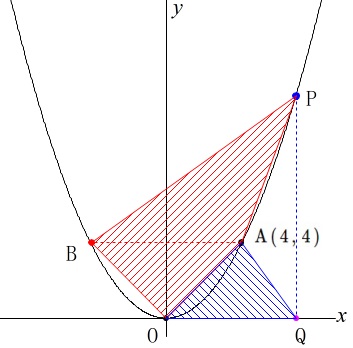
　四角形\(\,\mathrm{OAPB}\,\)の面積が\(\,\mathrm{△AOQ}\,\)の\(\,4\,\)倍になるとき、
言い換えると
　四角形\(\,\mathrm{OAPB}\,\)と\(\,\mathrm{△AOQ}\,\)の面積比が\(\,\color{red}{4}:\color{blue}{1}\,\)となるとき
の点\(\,\mathrm{P}\,\)の\(\,x\,\)座標を求めます。

\(\,y\,\)軸対称なので点\(\,\mathrm{B}\,\)の\(\,y\,\)座標は点\(\,\mathrm{A}\,\)と同じで
　\(\,\mathrm{B\,(\,-4\,,\,4\,)}\,\)

点\(\,\mathrm{P}\,\)の\(\,x\,\)座標を\(\,t\,\)とおくと、
（文字は何でも良いですよ。）
　\(\displaystyle \,\mathrm{P}\,\left(\,t\,,\,\frac{1}{4}\,t^2\,\right)\,\)
　\(\mathrm{Q}\,(\,t\,,\,0\,)\)

となります。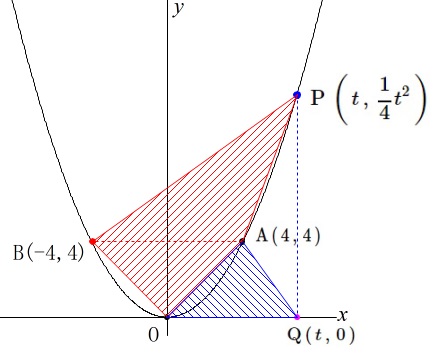それぞれの面積を文字で表しますが、分かる部分の長さを図に書き込みます。
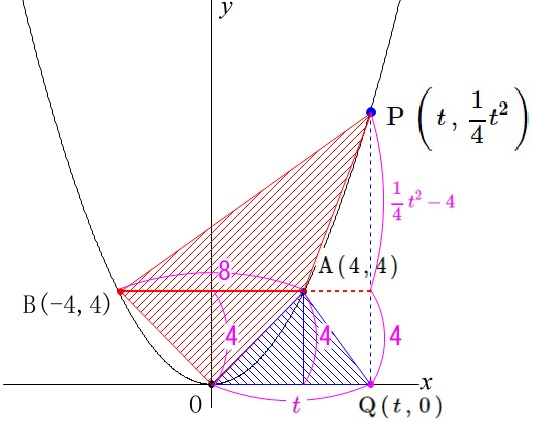四角形\(\,\mathrm{OAPB}\,\)と\(\,\mathrm{△AOQ}\,\)の面積は、それぞれ次のようになります。

　\(\begin{eqnarray}\displaystyle
四角形\mathrm{OAPB}&=&\mathrm{△OAB+△ABP}\\
&=&\frac{1}{2}\times 8\times 4+\frac{1}{2}\times 8\times (\frac{1}{4}t^2-4)\\
&=&16+t^2-16\\
&=&\color{red}{t^2}
\end{eqnarray}\)

　\(\begin{eqnarray}\displaystyle
\mathrm{△AOQ}&=&\frac{1}{2}\times t\times 4\\
&=&\color{blue}{2\,t}
\end{eqnarray}\)

ただし、これは点\(\,\mathrm{P}\,\)の\(\,x\,\)座標\(\,t\,\)が\(\,4\,\)より大きいものとしてあります。
※
点\(\,\mathrm{P}\,\)の\(\,x\,\)座標が負の場合も考えるときは、
\(\,\mathrm{△AOQ}\,\)の面積は絶対値が必要になるので符号が変わります。
四角形\(\,\mathrm{OAPB}\,\)の面積はそのままで構いません。

話を戻して、
　四角形\(\,\mathrm{OAPB}\,:\,\mathrm{△AOQ}\,=\color{red}{4}:\color{blue}{1}\)
のとき
　\(\begin{eqnarray}
\color{red}{t^2}:\color{blue}{2\,t}&=&\color{red}{4}:\color{blue}{1}\\
t^2&=&8\,t\\
t^2-8\,t&=&0\\
t\,(\,t-8\,)&=&0\\
t&=&0\,,\,8
\end{eqnarray}\)

ここで、\(\,t\,＞\,4\,\)なので
　\(\,t=8\,\)

つまり点\(\,\mathrm{P}\,\)の\(\,x\,\)座標が\(\,8\,\)のとき、
\(\,四角形\mathrm{OAPB}\,\)の面積が\(\,\mathrm{△AOQ}\,\)の面積の\(\,4\,\)倍になります。

答え　\(\,\underline{　8　}\,\)

点\(\,\mathrm{P}\,\)の\(\,x\,\)座標が負の場合にも面積比が\(\,4:1\,\)になる場合がありますが、
ここでは聞かれていないので関係ありません。
（注意はしておきましょう。）

座標の文字設定には慣れておいた方が良いですね。
『超え太郎』の「座標と図形」の単元を繰り返して慣れておけば、高校に進学しても関数の文字設定にほとんど困ることはありません。

⇒　一人でできる中学数学短期攻略教材『覚え太郎』

もちろん宣伝ですが、おすすめです。

⇒　2020年東京都立高校入試前期数学の平面図形問題の解説(第4問)

\(\color{black}{\fbox{　4　}}\)は平面図形ですがここまでは基本問題です。

⇒　東京都公立高校入試数学の過去問と解答解説

この年の数学の平均点は例年より高めではないでしょうか。