2020年東京都立高校入試前期数学の平面図形問題の解説(第4問)

2020年（令和2年）に行われた東京都立入試前期の第4問平面図形問題の解説です。
正方形があって、角度、合同な三角形の証明、および線分比を求める問題があります。
どれも基本問題なので、教科書の内容を理解していれば詳しい説明は必要ないでしょう。

\(\color{black}{\fbox{　4　}}\)の問題です。

⇒　2020年東京都立高校入試数学の第4問の問題

四角形\(\,\mathrm{ABCD}\,\)は正方形です。
正方形は平行四辺形であり、長方形であり、ひし形でもあります。

問題全体に通じる条件は
　四角形\(\,\mathrm{ABCD}\,\)は正方形
　\(\,\mathrm{CP=CQ}\,\)
です。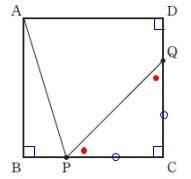

〔問１〕平行線の錯角は等しい

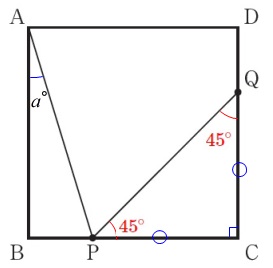
\(\,∠\mathrm{BAP}=a^{\circ}\,\)としたときの\(\,\mathrm{∠APQ}\,\)の大きさを求めます。

\(\,\mathrm{△CPQ}\,\)は直角二等辺三角形なので
　\(\,\mathrm{∠CPQ=∠CQP=\color{red}{45^{\circ}}}\,\)

ここまでは\(\,\mathrm{CP=CQ}\,\)という条件が与えられているのですぐに分かるでしょう。
ここからはいろいろな方向で答えがでますが、
平行線の錯角が等しくなる、という性質を利用した単純な方法で答えを出しておきます。

平行線の錯角を利用して角度を求める問題は教科書でもやったことあるでしょう。
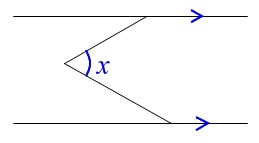このように平行線があって\(\,x\,\)を求める問題です。

平行線を引くんですよね。
同じことをします。

\(\,\mathrm{P}\,\)を通り、\(\,\mathrm{AB\,,\,DC}\,\)に平行な線を引くと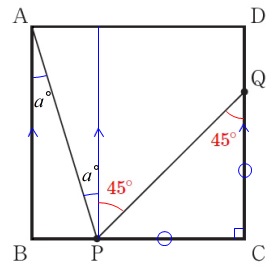平行線の錯角は等しいので、
　\(\begin{eqnarray}
\,\mathrm{∠APQ}\,&=&\,\mathrm{∠BAP+∠CQP}\,\\
&=&a^{\circ}+45^{\circ}\\
&=&(\,a+45\,)\,度
\end{eqnarray}\)

答え　\(\,\underline{　ウ　}\,\)

\(\,\mathrm{∠BPA}=90^{\circ}-a^{\circ}\,\)として、
　\(\,\mathrm{∠APQ=180^{\circ}-(∠BPQ+∠CPQ)}\,\)
から求めても良いですよ。

方程式にしても同じです。
\(\,\mathrm{∠APQ}=x\,\)とすると

　\(\begin{eqnarray}
90-a+x+45&=&180\\
x&=&180-135+a\\
&=&a+45
\end{eqnarray}\)

大した差はありませんが、錯角を利用するのが楽、でしょう。

〔問２〕合同の証明と相似な図形と線分比

図\(\,1\,\)の正方形に条件が加わります。

　\(\,\mathrm{AD=DE}\,\)
　直線\(\,\mathrm{EQ}\,\)と線分\(\,\mathrm{AP}\,\)との交点を\(\,\mathrm{R}\,\)

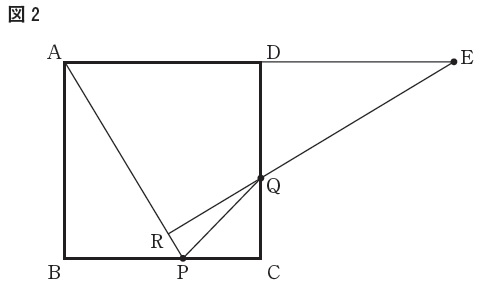
合同の証明手順

\(\,　①　\,\)合同の証明です。

　\(\,\mathrm{△ABP\,≡\,△EDQ}\,\)であることを証明します。

ここまでの条件を図に書き込みますが、
\(\,\mathrm{△CPQ}\,\)が直角二等辺三角形という条件は変わりません。

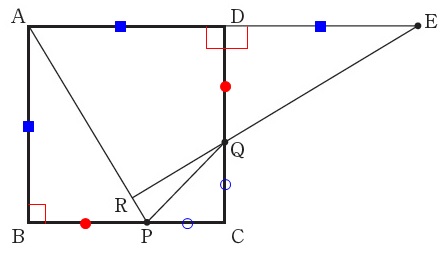すでに証明されていますが、一応説明しておきます。

　\(\,\mathrm{△ABP}\,\)と\(\,\mathrm{△EDQ}\,\)において
四角形\(\,\mathrm{ABCD}\,\)は正方形で
　\(\,\mathrm{\color{red}{AD}=\color{blue}{AB}}\,\)
仮定から\(\,\mathrm{\color{red}{AD}=\color{magenta}{DE}}\,\)なので
　\(\,\mathrm{\color{blue}{AB}=\color{magenta}{ED}　･･･①}\,\)

また、正方形であることから
　\(\,\mathrm{\color{blue}{BC}=\color{blue}{DC}}\,\)
および仮定から\(\,\mathrm{\color{magenta}{CP}=\color{magenta}{CQ}}\,\)
なので
　\(\,\mathrm{\color{red}{BP}=\color{blue}{BC}-\color{magenta}{CP}}\,\)
　\(\,\mathrm{\color{red}{DQ}=\color{blue}{DC}-\color{magenta}{CQ}}\,\)
であり、
　\(\,\mathrm{\color{red}{BP}=\color{red}{DQ}　･･･②}\,\)

さらに
　\(\,\mathrm{∠ABP=∠EDQ=90^{\circ}　･･･③}\,\)

①②③より
　\(\,2\,\)辺とその間の角がそれぞれ等しい
ので
　\(\,\mathrm{△ABP}\,≡\,\mathrm{△EDQ}\,\)

合同の証明や相似の証明は図の中で終わらせておくことです。
図で示せていないことを文章にするのは難しいですよ。
　

相似な図形と線分比の求め方

\(\,②\,\)　線分比を求めます。

①で合同を証明しているので利用するのだろう、という予想はしておいた方が良いですよ。
ただし、それだけで終わる単発問題ではありません。

長さの条件が加わります。

　\(\,\mathrm{AB=\color{red}{4}\,,\,BP=\color{red}{3}}\,\)
（単位は\(\,\mathrm{cm}\,\)ですが、必要無いので省略します。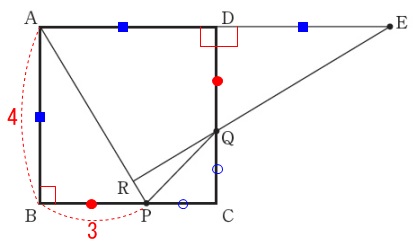）①から
　\(\,\mathrm{△ABP　≡　△EDQ}\,\)
なので、\(\,\mathrm{ED=\color{red}{4}\,,\,DQ=\color{red}{3}}\,\)
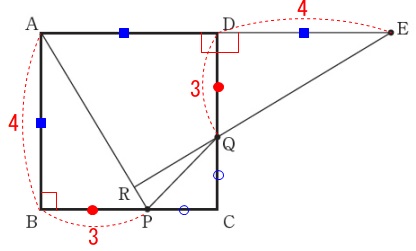　\(\,\mathrm{△EDQ}\,\)において三平方の定理から、
（比を覚えている場合は計算しなくて良いです。）

　\(\begin{eqnarray}
\mathrm{EQ^2}&=&\mathrm{ED^2+DQ}\\
&=&4^2+3^2\\
&=&25\\
\mathrm{EQ}&=&\pm 5
\end{eqnarray}\)

\(\,\mathrm{EQ}\,\)は長さなので\(\,\mathrm{BQ＞0}\,\)だから
　\(\mathrm{EQ}=\color{blue}{5}\)

\(\,\mathrm{AD=DE=4}\,\)であることも加えて図に示します。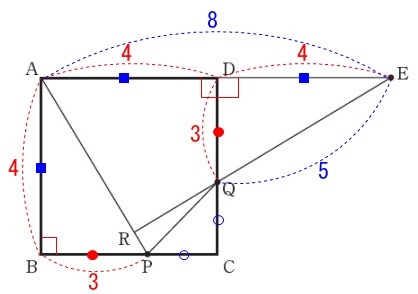
合同であることと正方形から明らかなように

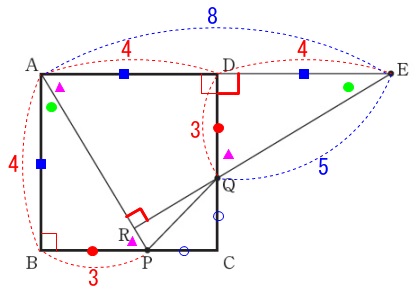
　\(\,\mathrm{△EDQ}\)　∽　\(\,\mathrm{△ERA}\,\)
このことから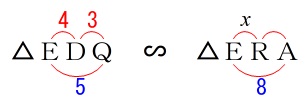　
　\(\begin{eqnarray}\displaystyle
\mathrm{ED:ER}&=&\mathrm{EQ:EA}\\
4:\mathrm{ER}&=&5:8\\
5\times \mathrm{ER}&=&8\times 4\\
\mathrm{ER}&=&\color{red}{\frac{32}{5}}
\end{eqnarray}\)

このとき
　\(\begin{eqnarray}\displaystyle
\mathrm{QR}&=&\mathrm{ER-EQ}\\
&=&\color{red}{\frac{32}{5}}-\color{blue}{5}\\
&=&\frac{32-25}{5}\\
&=&\color{magenta}{\frac{7}{5}}
\end{eqnarray}\)
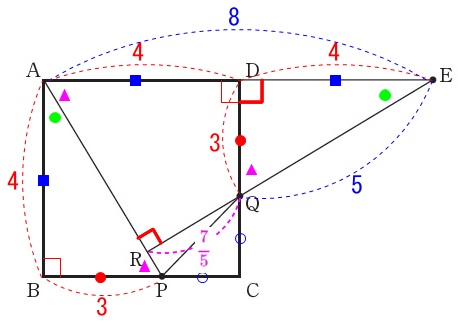　よって、
　\(\begin{eqnarray}\displaystyle
\mathrm{EQ:QR}&=&\color{blue}{5}:\color{magenta}{\frac{7}{5}}\\
&=&\underline{　25:7　}
\end{eqnarray}\)