2020年(令和2年)度東京都公立高校入試前期数学の問題と解説(第2問)

2020年(令和2年)度東京都公立高校入試前期数学の第2問の問題と解説です。
例年と同じく生徒と先生の問題の出し合いですが、単なる円柱の体積問題です。
具体的な数値ではなく文字式のまま処理するので、答えは選択と証明だから計算ミスはそれほど気にしなくて良いですね。

東京都立入試前期数学の第\(\,2\,\)問の問題です。

⇒　2020年東京都立高校入試前期第2問の問題

長い問題文ですが、展開図から立体をイメージしているかどうかを聞いている問題です。

〔問１〕2つの円柱の体積の差

問題に書いてありますが、図１図２は円柱の展開図です。

図１は底面の円の半径が\(\,a\,\)で、高さが\(\,h\,\)の円柱
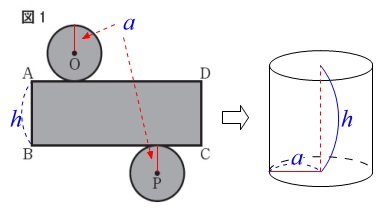図１は底面の円の半径が\(\,b\,\)で、高さが\(\,h\,\)の円柱

図１の円柱の体積\(\,\mathrm{X}\,\)は
　底面の面積が\(\,\pi\,a^2\,\)、高さが\(\,h\,\)
なので
　\(\hspace{10pt}\mathrm{\color{red}{X}}=\pi\,a^2\,h\)

図２の円柱の体積は
　底面の面積が\(\,\pi\,b^2\,\)、高さが\(\,h\,\)
なので
　\(\hspace{10pt}\mathrm{\color{blue}{Y}}=\pi\,b^2\,h\)

2つの円柱は高さが同じ\(\,\color{blue}{h}\,\)で、
底面の円の半径が\(\,\color{red}{a}＞\color{magenta}{b}\,\)なので、
図１の円柱の体積の方が大きいことは分かりますよね。

このことから
　\(\begin{eqnarray}
\mathrm{\color{red}{X}-\color{blue}{Y}}&=&\pi\,a^2\,h-\pi\,b^2\,h\\
&=&\pi\,h\,(a^2-b^2\,)
\end{eqnarray}\)

問題の答えの中に合わせると
　\(\,\underline{　ア　}\,\)　\(\,\pi\,(\,a^2-b^2\,)h\,\)

見取り図を書くか書かないかで問題の感じがものすごく変わることが分かるでしょう。

〔問２〕体積の和と差を文字式を利用して証明する問題

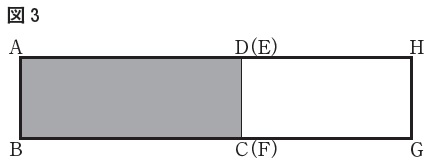
図３は図１の円柱と図２の円柱の側面をつなげた長方形です。
円柱の底面の周と側面の横の長さは等しくなるので、
　\(\hspace{10pt}\mathrm{\color{red}{AD}}=\color{red}{2a\,\pi}\,\)
　\(\hspace{10pt}\mathrm{\color{blue}{EH}}=\color{blue}{2b\,\pi}\,\)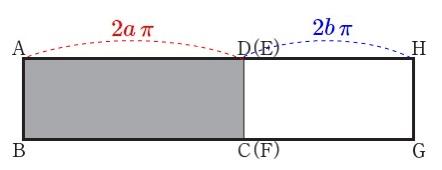

つまり、図３の長方形の横の長さは
　\(\hspace{10pt}\color{red}{2a\,\pi}+\color{blue}{2b\,\pi}=\color{magenta}{2(a+b)\,\pi}\)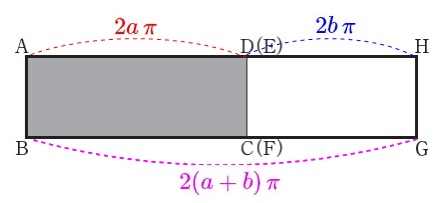
円の半径\(\,r\,\)と円周\(\,\ell\,\)との関係は
　\(\hspace{10pt}\ell=2\,\pi \,r=2\,r\,\pi\)
なので図４の円柱の底面の半径は円周が\(\,\color{magenta}{2(a+b)\,\pi}\,\)であることから
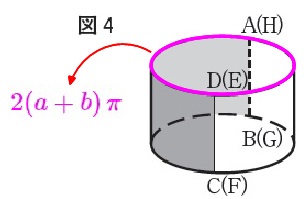図４の円柱の底面の半径\(\,\color{red}{r}\,\)は
　\(\begin{eqnarray}
2\,\color{red}{r}\,\pi&=&\color{magenta}{2\,(\,a+b\,)\,\pi}\\
\color{red}{r}&=&\color{red}{a+b}
\end{eqnarray}\)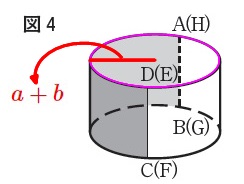高さは\(\,\color{blue}{h}\,\)なので、

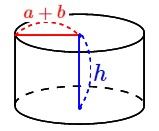
図４の円柱の体積\(\,\mathrm{Z}\,\)は

　\(\begin{eqnarray}
\mathrm{Z}&=&\pi\,(\,\color{red}{a+b}\,)^2\times \color{blue}{h}\\
&=&\color{magenta}{\pi\,(\,a+b\,)^2\,h}
\end{eqnarray}\)

また、図１の円柱と図２の円柱の体積の和\(\,\mathrm{W}\,\)は

　\(\hspace{10pt}\mathrm{W}=\color{blue}{\pi\,a^2\,h+\pi\,b^2\,h}\)

よって、
　\(\begin{eqnarray}
\mathrm{Z-W}&=&\color{magenta}{\pi\,(\,a+b\,)^2\,h}-(\color{blue}{\pi\,a^2\,h+\pi\,b^2\,h})\\
&=&\pi\,h\,\color{magenta}{(a+b)^2}-\pi\,h\,(\,\color{blue}{a^2+b^2}\,)\\
&=&\pi\,h\,\{(a+b)^2-(a^2+b^2)\}\\
&=&\pi\,h(a^2+2ab+b^2-a^2-b^2)\\
&=&\pi\,h\,(2ab)\\
&=&2\,\pi\,a\,b\,h
\end{eqnarray}\)
（証明終わり）

3行目で\(\,\{\,\)中かっこ\(\,\}\,\)を使っているのでわかりにくければ、
　\(\begin{eqnarray}
\mathrm{Z}&=&\pi\,(\,\color{red}{a+b}\,)^2\times \color{blue}{h}\\
&=&\pi\,h\,(\,a^2+2ab+b^2\,)
\end{eqnarray}\)
と展開しておいて、
　\(\begin{eqnarray}
\mathrm{Z-W}&=&\pi\,h\,(\,a^2+2ab+b^2\,)-(\pi\,a^2\,h+\pi\,b^2\,h)\\
&=&\pi\,h\,(a^2+2ab+b^2)-\pi\,h\,(\,a^2+b^2\,)\\
&=&\pi\,h\,(a^2+2ab+b^2-a^2-b^2)\\
&=&2\,\pi\,a\,b\,h
\end{eqnarray}\)
としても良いです。

どっちもにたようなものですけど。笑

長々と説明する問題でもないのですが、
部分的に必要なところを抜き取ってまとめれば証明になります。
ただ、文字式がややこしいので難しいという思い込みだけはしないようにしてください。

先ずは分かることを書き出してみることです。
そうすれば証明は終わっていますよ。

⇒　2020年東京都立高校入試前期数学の関数問題の解説(第3問)

\(\color{black}{\fbox{　3　}}\)は関数の問題です。

⇒　東京都公立高校入試数学の過去問と解答解説

問題内容は変わっても問題構成と基本的なことを聞いてくるのは毎年同じです。