2020年東京都立高校入試前期数学の第5問立体問題の解説

2020年（令和2年）に行われた東京都立入試前期の第5問立体問題の解説です。
空間図形も平面図形の組み合わせなので利用する基本は平面と同じです。
ポイントは三平方の定理の利用と四角錐の体積の高さとなる垂線を求めるだけですが、錐体の体積の基本に戻ると別解が見えてきます。

\(\color{black}{\fbox{　5　}}\)の問題です。

⇒　2020年東京都立高校前期入試の数学第5問の問題

見つけいにくいのは〔問２〕の四角錐の体積を求めるときの高さですが、
平面として抜き出せば基本的な相似問題になります。

最初から長さの条件が与えられているので確認しておきます。

　\(\,\mathrm{ABCD-EFGH}\,\)は直方体
　\(\,\mathrm{AB=6\,,\,AD=8\,,\,AE=12}\,\)
（単位は省略しておきます。）
　点\(\,\mathrm{P}\,\)は線分\(\,\mathrm{CF}\,\)上の点
　点\(\,\mathrm{Q}\,\)は辺\(\,\mathrm{AB}\,\)上の点（\(\,\mathrm{B}\,\)には一致しない）

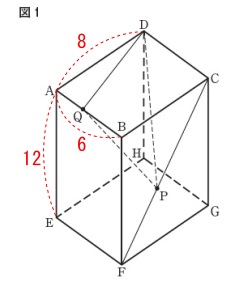
〔問１直角三角形の面積〕

〔問１〕点\(\,\mathrm{P}\,\)が頂点\(\,\mathrm{F}\,\)にあり、
点\(\,\mathrm{Q}\,\)が頂点\(\,\mathrm{A}\,\)に一致するときの\(\,\mathrm{△DQP}\,\)の面積を求めます。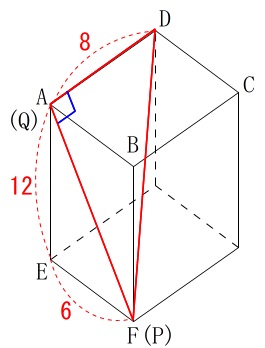このとき、（\(\,\mathrm{ABCD-EFGH}\,\)は直方体）
　辺\(\,\mathrm{DA}\,\)（辺\(\,\mathrm{DQ}\,\)）と面\(\,\mathrm{AEFB}\,\)は垂直
なので、
　辺\(\,\mathrm{DQ}\,\)と辺\(\,\mathrm{AF}\,\)（辺\(\,\mathrm{PQ}\,\)）も垂直
になっています。

つまり、\(\,\mathrm{△DQP}\,\)は直角三角形なので面積は簡単に求まります。

三平方の定理から
　\(\begin{eqnarray}
\mathrm{PQ^2}&=&\mathrm{AE^2+EF^2}\\
&=&12^2+6^2\\
&=&144+36\\
&=&180\\
\mathrm{PQ}&=&\pm 6\sqrt{5}
\end{eqnarray}\)

\(\,\mathrm{PQ}\,\)は長さだから\(\,\mathrm{PQ＞0}\,\)で
　\(\mathrm{PQ}=\color{blue}{6\sqrt{5}}\)

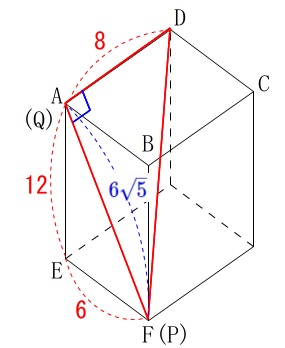よって
　\(\begin{eqnarray}\displaystyle
\mathrm{△DQP}&=&\frac{1}{2}\times \mathrm{PQ}\times \mathrm{DQ}\\
&=&\frac{1}{2}\times \color{blue}{6\sqrt{5}}\times \color{red}{8}\\
&=&\color{black}{\fbox{　\(\,24\,\)　}}\sqrt{\color{black}{\fbox{　\(\,5\,\)　}}}　
\end{eqnarray}\)

答え　くけ　\(\,\underline{　24　}\,\)　こ　\(\,\underline{　5　}\,\)

ここまではすんなり進んだでしょう。
図に点\(\,\mathrm{P}\,\)や点\(\,\mathrm{Q}\,\)を書き込みさえすればですけどね。

〔問２〕の求め方がいろいろとあるので、めんどくさ、、、いわけではないけれど、
どれが適切なのか、理解しやすいのか人によって違ってくるでしょう。
何度も言っていることですが、数学の答えは１つでも、求め方は１つではないんですよ。

〔問２〕四角錐の体積のお求め方

〔問２〕は立体\(\,\mathrm{P-DQRH}\,\)の体積、つまり四角錐の体積を求める問題です。

条件が加わります。

　点\(\,\mathrm{Q}\,\)を通り\(\,\mathrm{AE}\,\)に平行な線と\(\,\mathrm{EF}\,\)との交点を\(\,\mathrm{R}\,\)
　\(\,\mathrm{AQ=4}\,\)
　\(\,\mathrm{CP:PF=3:5}\,\)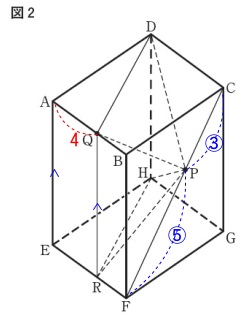
求める立体が四角錐なので、
　底面積\(\,\mathrm{DQRH}\,\)の面積と高さ\(\,h\,\)
を求める方法が考えられます。
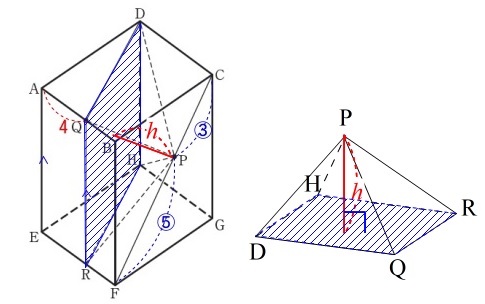このとき底面となる四角形\(\,\mathrm{DQRH}\,\)は長方形です。
問題なのは高さとなる\(\,h\,\)です。

これは点\(\,\mathrm{P}\,\)を通る面\(\,\mathrm{ABCD}\,\)に平行な面で切り取れば分かるのですが、
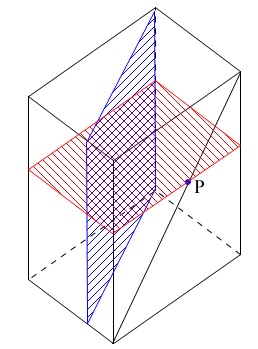いきなりだとわかりにくいと思うので少し説明しておきます。

例えば点\(\,\mathrm{P}\,\)が頂点\(\,\mathrm{C}\,\)にあるとき、
面\(\,\mathrm{ABCD}\,\)と面\(\,\mathrm{DQRH}\,\)は面どうしが垂直なので、
点\(\,\mathrm{P}\,\)から面\(\,\mathrm{DQ}\,\)に垂線を下ろすとそれが高さになります。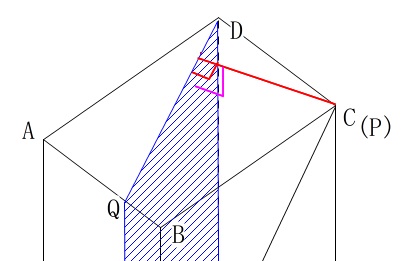錐体の高さは頂点と底面との距離で、
「最短距離」を意味しているので垂直に下りていなくてはなりません。
（底面を水平にしていれば頂点から水を垂らして落下する点までの距離が高さです。）

点\(\,\mathrm{P}\,\)が線分\(\,\mathrm{CF}\,\)上を移動した場合、
点\(\,\mathrm{C}\,\)から面\(\,\mathrm{ABCD}\,\)に下ろした垂線と平行に移動することになるので、
高さとなる垂線は面\(\,\mathrm{ABCD}\,\)に平行になります。
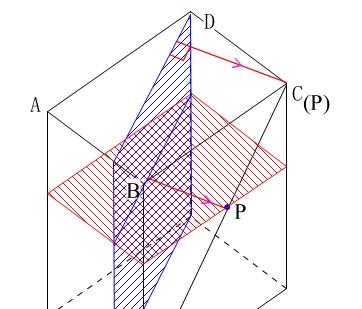点\(\,\mathrm{P}\,\)が\(\,\mathrm{CP:PF=3:5}\,\)という条件を満たしたときの垂線は、
相似を使えば簡単に求まります。

三平方の定理から
　\(\begin{eqnarray}
\mathrm{DQ^2}&=&\mathrm{AD^2+AB^2}\\
&=&8^2+6^2\\
&=&80\\
\mathrm{DQ}&=&\color{blue}{4\sqrt{5}}　（＞0）
\end{eqnarray}\)

なので分かる部分の長さを書き込みます。
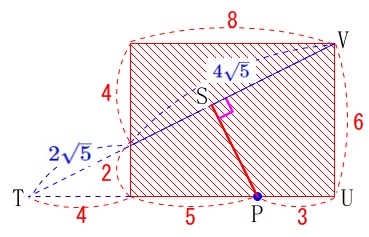相似を使って長さを出すのはどの相似でも良いです。
面積を出して底辺を変えるという回りくどい方法もありますが相似を利用した方が早いです。
ここでは簡単そうだったので下の図の部分から長さを出しました。
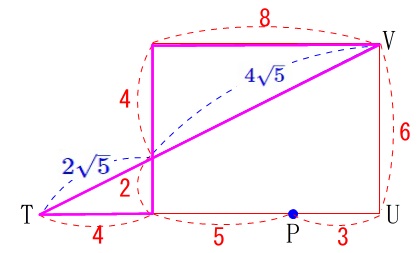では、高さとなる\(\,\mathrm{PS}\,\)を求めに行きましょう。
　\(\,\mathrm{△TSP}\,\)　∽　\(\,\mathrm{△TUV}\,\)
なので、
　\(\begin{eqnarray}
\mathrm{TP:TV}&=&\mathrm{PS:VU}\\
(\color{red}{4}+\color{red}{5}):(\color{blue}{2\sqrt{5}}+\color{blue}{4\sqrt{5}})&=&PS:6\\
9:6\sqrt{5}&=&\mathrm{PS}:6\\
6\sqrt{5}\mathrm{PS}&=&9\times 6\\
\mathrm{PS}&=&\frac{9\times 6}{6\sqrt{5}}\\
&=&\color{magenta}{\frac{9}{\sqrt{5}}}
\end{eqnarray}\)

分母は有理化しても良いですが、
底面の長方形\(\,\mathrm{DQRH}\,\)の面積は
　
　\(\begin{eqnarray}
　(長方形\mathrm{DQRH})&=&\,\mathrm{DQ}\times \mathrm{QR}\,\\
&=&\color{blue}{4\sqrt{5}\times 12}
\end{eqnarray}\)

だから約分できるのでそのままかけることにします。

これは底面である長方形の面積を先に出しておけば気がつくことなので、
順番としてはおかしくはないでしょう。
高さが問題になるということで、高さの話を先にしただけです。
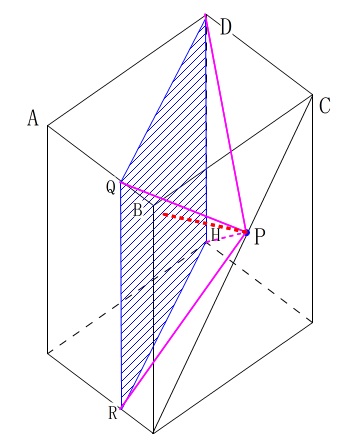よって、求める立体\(\,\mathrm{P-DQRH}\,\)の体積\(\,V\,\)は
　\(\begin{eqnarray}
V&=&\frac{1}{3}\times\color{blue}{ 4\sqrt{5}\times 12}\times \color{magenta}{\frac{9}{\sqrt{5}}}\\
&=&\underline{　144　}
\end{eqnarray}\)

答え　\(\color{black}{\fbox{ さしす }}\)　\(\,\underline{　144　}\,\)

これが一番普通でしょう。

〔問２の別解〕

他にもいくつか方法はありますが、
　四角錐の体積は四角柱の体積の\(\displaystyle \,\mathrm{\frac{1}{3}}\,\)
ということから考えると、元になる四角柱は、
　長方形\(\,\mathrm{DQRH}\,\)と平行な面で点\(\,\mathrm{P}\,\)を通る長方形
で作られる四角柱になります。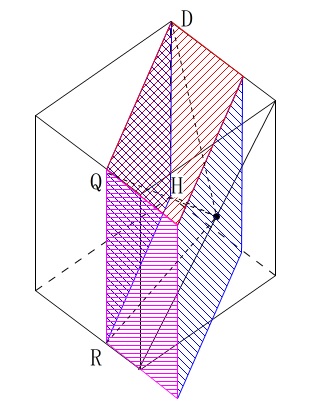

ちょっと説明を省きますが、
長方形\(\,\mathrm{DQRH}\,\)と平行になる長方形\(\,\mathrm{WXYZ}\,\)は
　\(\,\mathrm{CP:PF=3:5}\,\)
となる点\(\,\mathrm{P}\,\)を通るので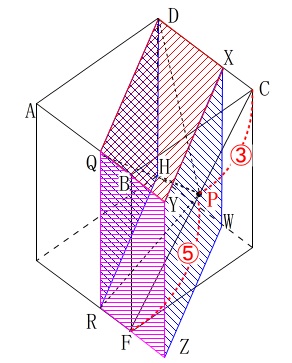平面\(\,\mathrm{ABCD}\,\)を抜き出すと、
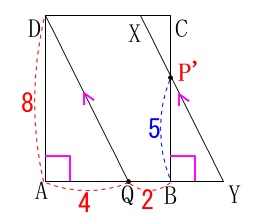\(\,\mathrm{△AQD}\,\)と\(\,\mathrm{△BYP’}\,\)が相似なので線分\(\,\mathrm{QY}\,\)の長さが簡単に求まるので、
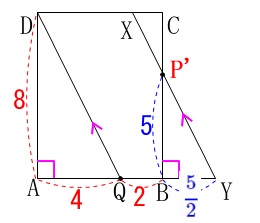平行四辺形\(\,\mathrm{DQYX}\,\)の面積が求まります。

　\(\begin{eqnarray}\displaystyle
(\mathrm{DQYX})&=&\mathrm{QY}\times \mathrm{AD}\\
&=&\left(\color{red}{2}+\color{blue}{\frac{5}{2}}\right)\times \color{red}{8}\\
&=&\frac{9}{2}\times 8
\end{eqnarray}\)

四角柱の体積はこれに高さとなる\(\,\mathrm{AE=12}\,\)をかけて

　\(\displaystyle \frac{9}{2}\times 8\times 12\)

よって求める錐体の体積\(\,V\,\)は
　\(\begin{eqnarray}\displaystyle
V&=&\frac{1}{3}\times \frac{9}{2}\times 8\times 12\\
&=&\underline{　144　}
\end{eqnarray}\)

でも良いです。

泥くさくても答えを出すことが優先される試験会場だと、
　\(\,(部分)=(全体)-(部分)\,\)
なので四角柱から4つの錐体を引いても良いですね。
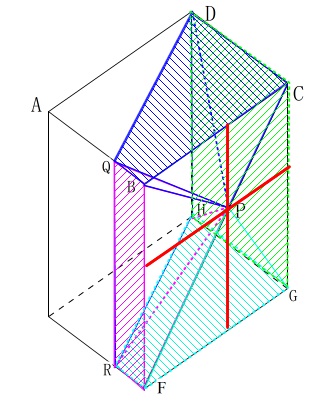（赤線は引く錐体の高さとなる部分です。）
それほどややこしい計算はありません。

もう一つ、最初に解いた四角錐の高さは、
　点\(\,\mathrm{P}\,\)が頂点\(\,\mathrm{C}\,\)にあるとき
と
　点\(\,\mathrm{P}\,\)が頂点\(\,\mathrm{F}\,\)にあるとき
の垂線の長さから
　点\(\,\mathrm{P}\,\)が\(\,\mathrm{CP:PF=3:5}\,\)となるとき
の長さを求めて体積を出しました。確認して見てください。