2020年(令和2年)度埼玉県公立高校一般入試の数学問題と解説

2020年(令和2年)度に行われた埼玉県公立高校一般入試の数学問題と解説です。
第3問，第4問は学校選択問題と同じ問題なので、学校選択問題の解説の一部はこちらを見ておいてください。
昨年度との違いは、幅広い基本的な数学の習得度を測る公立高校らしい入試問題になった、ということでしょう。

埼玉県が公開してくれている一般入試数学の問題です。

⇒　2020年(令和2年)度埼玉県公立高校一般入試数学の問題

埼玉県の解説を昨年度までは\(\,\mathrm{VIP}\,\)会員の方にお任せしておりましたが、再現に時間がかかる（らしい）、知り合いの方も無事合格されたということで、\(\,2020\,\)年度からは私がこのサイトで直に書くことにします。

昨年度との違いを冒頭で書きましたが、業者の匂いが消えた、という感じがしただけです。
埼玉県はずいぶん前から高校入試に業者が関与していると有名でしたので、なんとなくですが公立、公平になってきているのかな、と。

まあ、そんなことは毎年行われる受験の結果に関係ありませんが、
今年、通塾生を除いて全国で\(\,1\,\)番最初に当会へご報告をくれたのは、埼玉県の難関高校受験生の合格報告でした。
ありがとうございました。

では、一般入試の数学問題解説を始めます。
解いていけば、「あれ、もう終わり？」となりますが、解説するとなると長くなるので分けるかもしれません。笑
（この時点では一気に行く予定です。が、たぶん長くなります。笑）

『覚え太郎』シリーズで勉強している人にそれほど解説は必要ない問題ですね。

第１問小問集合

\(\color{black}{\fbox{　1　}}\)はいろいろな分野の基本用語に関する小問集合です。

式の計算・方程式

\(\,(1)\,\)同類項をまとめます。
　\(\hspace{10pt}7x-5x\\
=\underline{　2x　}\)

\(\,(2)\,\)足し算引き算よりかけ算割り算が先です。
　\(\hspace{10pt}\color{red}{(-5)\times (-2)}+3\\
=\color{red}{10}+3\\
=\underline{　13　}\)

\(\,(3)\,\)文字式計算の基礎です。
割り算は分数計算にします。\(\,「\div」\,\)（割る）の直後が分母になります。
　\(\hspace{10pt}6x\times 2xy\color{red}{\div 3y}\\
=\displaystyle \frac{6x\times 2xy}{\color{red}{3y}}\\
=\underline{　4x^2　}\)

\(\,(4)\,\)
\(\,1\,\)次方程式です。
方程式の基本はすべての項を左辺に集めることですが、
\(\,1\,\)次方程式は\(\,1\,\)次の項を左辺に、定数項を右辺に集めると早いです。
　\(\begin{eqnarray}
5x+3&=&2x+6\\
5x-2x&=&6-3\\
3x&=&3\\
x&=&1
\end{eqnarray}\)

ちょっとしたポイントなのですが、方程式の処理をするときに、
\(5x+3=2x+6\\
5x-2x=6-3\\
3x=3\\
x=1\)
と、文字の最初をそろえるより、等号（\(\,=\,\)）をそろえるときれいに見えます。笑
きれいに見えるということは全体の処理も早くなり、計算ミスも減るということです。

まあ、この程度のことは学校でも普通の塾でも最初にいわれているだろうからいうまでもありませんね。

\(\,(5)\,\)無理数の計算です。
　\(\hspace{10pt}\color{red}{\sqrt{18}}-6\sqrt{2}\\
=\color{red}{3\sqrt{2}}-6\sqrt{2}\\
=\underline{　-3\sqrt{2}　}\)

無理数は根号（ルート）の中が違う数字のときは足し算引き算できません。
素因数分解はきっちりやって計算ミスをしないようにしましょう。

\(\,(6)\,\)\(\,2\,\)次式の因数分解です。
定数項\(\,-12\,\)に着目ですね。
　\(\color{black}{\fbox{\(\,1\times 12\,\)}}\)　\(\color{red}{\fbox{\(\,2\times 6\,\)}}\)　\(\color{black}{\fbox{\(\,3\times 4\,\)}}\)
のどちらかの因数に\(\,－\,\)を着けて\(\,1\,\)次の項の係数\(\,+4\,\)になるようにすれば良いだけです。
　\(\,-\,2\,\)　と　\(\,+\,6\,\)　の組合わせで\(\,+\,4\,\)になります。
　\(\hspace{10pt}x^2+4x-12\\
=\underline{　(x-2)(x+6)　}\)

答えは\(\,\underline{　(x+6)(x-2)　}\,\)の順番でも良いですよ。
因数の順序に問題の指定はありません。
※
問題\(\,1\,\)枚目の注意事項は各都道府県で毎年それほど変わるわけではありませんので、受験前に必ず確認しておくようにしましょう。
もちろん試験本番でも変更点があるかもしれないので再度確認はしておきましょう。

\(\,(7)\,\)連立方程式です。
解を求める単なる計算処理なので、一文字消去が基本です。
　　\( \begin{cases}
\hspace{7pt} 6x-\hspace{4pt}y=1\\ \\
\hspace{7pt} 3x-2y=-7
\end{cases}\)

どちらを消去するのでも大した差はありません。
先に\(\,y\,\)を消去する方向で説明します。

上の第一方程式を\(\,2\,\)倍して下の第二方程式を左辺右辺ともに引きます。
　\(\hspace{10pt}12x-2y=2\\
\underline{-\,)\,3x-2y=-7}\\
\hspace{14pt}9x\hspace{22pt}=9\\
\hspace{40pt}x=\underline{　\color{red}{1}　}\)

これをどの方程式でも良いので代入すると\(\,y\,\)が求まります。
一番上の方程式に代入すると、
　\(\begin{eqnarray}
6\times (\color{red}{1})-y&=&1\\
6-y&=&1\\
-y&=&-5\\
y&=&\underline{　5　}
\end{eqnarray}\)

代入するときは正の数でも負の数でも（かっこ）を着けて代入するようにしておくと計算ミスが減りますよ。

もちろん、\(\,x\,\)を最初に消去する、でも同じなのでやってみてください。
問題集の解説がどうなっていようが、解を導く方法が1つだけということはありません。

\(\,(8)\,\)２次方程式です。
すべての項を左辺に集めてありますが左辺が因数分解できないので解の公式ですね。

⇒　２次方程式を解の公式で解く問題の見分け方と例題

２次方程式は
　\(\color{red}{3}x^2\color{blue}{-5}x\color{magenta}{+1}=0\)
なので
　\(\begin{eqnarray}\displaystyle
x&=&\frac{-(\color{blue}{-5})\pm \sqrt{(\color{blue}{-5})^2-4\times \color{red}{3}\times \color{magenta}{1}}}{2\times 3}\\
&=&\frac{5\pm \sqrt{25-12}}{6}\\
&=&\underline{　\frac{5\pm \sqrt{13}}{6}　}
\end{eqnarray}\)

平面図形・変化の割合・空間図形

\(\,(9)\,\)教科書でよく見る平行線と角度の問題です。
角のある所で平行線を引けば錯角が使えて早いです。
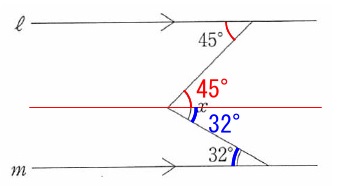平行線の場合は錯角が等しいので、
　\(\begin{eqnarray}
x&=&45^{\circ}+32^{\circ}\\
&=&\underline{　77^{\circ}　}
\end{eqnarray}\)

線分を延長するのも1つの手です。
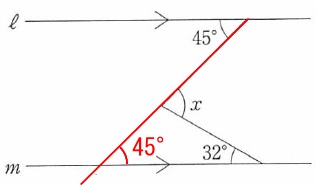何でも良いです。思いついた方法で一つひとつ角度を求めていけばほとんどの角度を求める問題は答えが出ます。

\(\,(10)\,\)変化の割合は、\(\,1\,\)次関数の傾きと同じです。
　\((変化の割合)=\displaystyle \frac{　(\color{red}{\,y\,の増加量})　}{　(\color{blue}{\,x\,の増加量})　}\)

関数\(\,y=2x^2\,\)において
　\(\,x=2\,\)のとき\(\,y=2(2)^2=8\,\)
　\(\,x=4\,\)のとき\(\,y=2(4)^2=32\,\)
なので
　\((\,x\,の増加量)=4-2=\color{blue}{2}\)
　\((\,y\,の増加量)=32-8=\color{red}{24}\)
※
この増加量を計算するときは必ず同じ向きに引き算しないと変化の割合の符号が変わります。

　\((変化の割合)=\displaystyle \frac{\color{red}{24}}{\color{blue}{2}}=\underline{　12　}\)
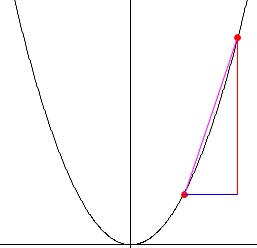グラフは適当なもので良いので\(\,2\,\)点を書き込み、
プラスかマイナスかくらいは見ておくといいですね。

\(\,(11)\,\)「ねじれの位置」とは平行でもなく、交わりもしないことです。

⇒　空間図形の位置関係問題(平行,ねじれの位置,垂直な面,平行な面)

線分を延長して交わっているものはねじれの位置とはいいませんがこの問題では気にする必要はありません。
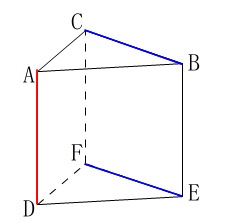ねじれの位置にある辺は2つありますが、選ぶ答えの中には1つしかありません。

　答え　\(\,\underline{　エ　}\,\)　辺\(\,\mathrm{BC}\,\)

反比例のグラフの性質と円錐の高さと体積

\(\,(12)\,\)反比例のグラフの性質に関する問題です。
誤っているものを1つ選ぶ問題なのでどれか1つを見つければ他は正しいということですが、
すべて見ていくことにします。

関数は\(\displaystyle \,y=\frac{6}{x}\,\)です。

\(\,ア\,\)　グラフは点\(\,(\,2\,,\,3\,)\,\)を通る。

グラフがその点を通るかどうかは関数を満たしているかどうかです。

\(\,(\,\color{red}{2}\,,\,\color{blue}{3}\,)\,\)を\(\displaystyle \,y=\frac{6}{x}\,\)に代入すると
　\(\displaystyle \color{blue}{3}=\frac{6}{\color{red}{2}}\)
で満たしています。（「点\(\,(\,2\,,\,3\,)\,\)を通る。」ということです。）

\(\,イ\,\)　グラフは原点中心の点対称である。

反比例のグラフは原点中心の点対称です。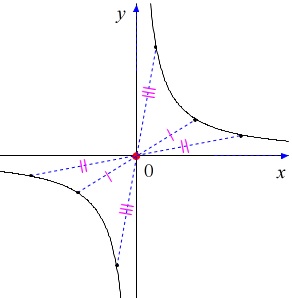
\(\,ウ\,\)　\(\,x＜0\,\)の範囲で変化の割合は一定である。

変化の割合は2点を通る直線の傾きと同じなので一定ではありません。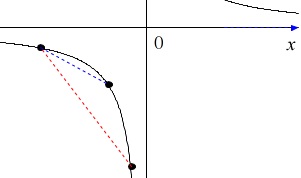
これは\(\,x＜0\,\)の範囲に限ったことではありません。
反比例のグラフで一定になるのはグラフ上の1つの点と、\(\,x\,\)軸、\(\,y\,\)軸と平行な線分で作る長方形の面積です。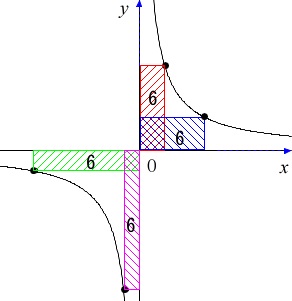すべての長方形が比例定数\(\,6\,\)になります。

だから誤りの答えは　\(\,\underline{　ウ　}\,\)

\(\,エ\,\)　\(\,x＜0\,\)の範囲で\(\,x\,\)が増加すると\(\,y\,\)は減少する。

言い換えれば\(\,x＜0\,\)の範囲（\(\,y\,\)軸より左側）で、
右に移動すればグラフは下がる、ということです。
正しいです。

\(\,(13)\,\)円すいの高さと体積を求めます。
底面の半径と母線の長さが与えられているのですぐに終わります。
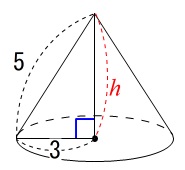母線を斜辺とする直角三角形の比が\(\,3:4:5\,\)になることを覚えていればすぐに終わりますが、
三平方の定理を利用して求めておきます。

円錐の高さを\(\,h\,\)とすると
　\(\begin{eqnarray}
h^2+3^2&=&5^2\\
h^2&=&25-9\\
&=&16\\
h&=&\pm 4
\end{eqnarray}\)

\(\,h\,\)は長さなので\(\,h＞0\,\)だから
　\(\hspace{10pt}h=\underline{　4　}\)

あと1つ錐体の体積は柱体の\(\displaystyle \frac{1}{3}\)なので
求める円錐の体積を\(\,V\,\)とすると
　底面積　\(\pi \times (3)^2\)
　高さ　\(h=4\)
なので
　\(\begin{eqnarray}\displaystyle
V&=&\frac{1}{3}\times \pi \times (3)^2\times 4\\
&=&12\,\pi
\end{eqnarray}\)

確率と代表値と標本

\(\,(14)\,\)さいころ2つの確率問題です。
確率問題なので樹形図でも良いですが、さいころ2つの場合は表を使うと早いです。

さいころは、\(\,1\,\)から\(\,6\,\)までの普通のさいころです。
大きいさいころの出た目を\(\,a\,\)、小さいさいころの出た目を\(\,b\,\)として、\(\,a＞b\,\)となる確率を求めますが大小逆でも確率は同じですね。

出た目のすべての場合を表にしておきます。
どちらでも同じですが
　数字が赤は大のさいころの出た目\(\,\color{red}{a}\,\)
　数字が青は小のさいころの出た目\(\,\color{blue}{b}\,\)
と見てください。

条件\(\,\color{red}{a}＞\color{blue}{b}\,\)となる場合を\(\,\color{magenta}{●}\,\)で印をしておきます。
　\(\begin{array}{|c|c|c|c|c|c|c|} \hline
& \color{red}{1} & \color{red}{2} & \color{red}{3} & \color{red}{4} & \color{red}{5} & \color{red}{6} \\ \hline
\color{blue}{1} & & \color{magenta}{●} & \color{magenta}{●} & \color{magenta}{●} & \color{magenta}{●} & \color{magenta}{●} \\ \hline
\color{blue}{2} & & & \color{magenta}{●} & \color{magenta}{●} & \color{magenta}{●} & \color{magenta}{●} \\ \hline
\color{blue}{3} & & & & \color{magenta}{●} & \color{magenta}{●} & \color{magenta}{●} \\ \hline
\color{blue}{4} & & & & & \color{magenta}{●} & \color{magenta}{●} \\ \hline
\color{blue}{5} & & & & & & \color{magenta}{●} \\ \hline
\color{blue}{6} & & & & & & \\ \hline
\end{array}\)

全部で\(\,36\,\)通りの場合があるので
　\(\displaystyle \frac{15}{36}=\underline{　\frac{5}{12}　}\)

この表を書き慣れてくると
　\(\color{red}{a}=\color{blue}{b}\)の場合（\(\,×\,\)）を除いて対称
になっているので
　（\(\,a＞b\,\)の場合\(\,\color{magenta}{●}\,\)と\(\,a＜b\,\)の場合\(\,○\,\)が同じだけある）
　\(\begin{array}{|c|c|c|c|c|c|c|} \hline
& \color{red}{1} & \color{red}{2} & \color{red}{3} & \color{red}{4} & \color{red}{5} & \color{red}{6} \\ \hline
\color{blue}{1} & × & \color{magenta}{●} & \color{magenta}{●} & \color{magenta}{●} & \color{magenta}{●} & \color{magenta}{●} \\ \hline
\color{blue}{2} & ○ & × & \color{magenta}{●} & \color{magenta}{●} & \color{magenta}{●} & \color{magenta}{●} \\ \hline
\color{blue}{3} & ○ & ○ & × & \color{magenta}{●} & \color{magenta}{●} & \color{magenta}{●} \\ \hline
\color{blue}{4} & ○ & ○ & ○ & × & \color{magenta}{●} & \color{magenta}{●} \\ \hline
\color{blue}{5} & ○ & ○ & ○ & ○ & × & \color{magenta}{●} \\ \hline
\color{blue}{6} & ○ & ○ & ○ & ○ & ○ & × \\ \hline
\end{array}\)

を思い浮かべて（表を書かずに）
　\(\displaystyle \frac{36-6}{36}\times \frac{1}{2}=\frac{5}{12}\)
と求めることもできますが、表を書くか、樹形図を書いた方が確実です。

(15)データの活用の代表値、平均値と中央値を求める問題です。

⇒　代表値とは？度数分布表の平均値,中央値の求め方と最頻値の答え方

具体的な数値データは小さい順か、大きい順に並べるのが基本です。

\(\,5\,\)人の成功した回数
　\(\,5\,,\,4\,,\,7\,,\,5\,,\,9\,\)

小さい順に並べ替えると
　\(\,4\,,\,5\,,\,5\,,\,7\,,\,9\,\)

中央値は並び替えたデータの真ん中の値なので
　\(\,\underline{　5　}\,\)

平均値は総得点を度数合計で割れば良いので、
　\(\displaystyle \frac{4+5+5+7+9}{5}\\
\displaystyle =\frac{30}{5}=\underline{　6　}\)

度数が少なく、奇数なので引っかかることもありませんね。

\(\,(16)\,\)標本の正しい選び方を選ぶ問題です。
標本を採るときは、「特定」ということを無くすことがポイントです。
ある条件をつけて抽出しないということです。

『全校生徒』の調査なので、『\(\,3\,\)年生』などの条件が付くと抽出（選び方）としては正しくありません。

正しいのは　\(\,\underline{　イ　}\,\)

「乱数さい」というのはさいころの1つで正二十面体でできています。
このさいころに\(\,0\,\)から\(\,9\,\)までの\(\,10\,\)個の各数字が二十面に\(\,2\,\)回ずつ印されたさいころだと思ってください。
　\(\,0\,が\,2\,面、\,1\,が\,2\,面、\cdots 、\,9\,が\,2\,面の合計\,20\,面\)

正多面体だからどの数字も同じ確率で出るということと、十進数が\(\,10\,\)個の数字を使うということから倍数の\(\,20\,\)面というのが便利な所です。
（正多面体は\(\,4,6,8,12,20\,\)しか無いですよ。）

\(\,1\,\)回ふれば一桁、\(\,2\,\)回振れば二桁、\(\,3\,\)回降れば三桁とふる回数を増やせば、
大きな桁数の数もランダムに（無作為に）作れるというさいころです。

\(\,600\,\)人なので\(\,000\,～\,599\,\)までの通し番号を付け、
百の位は普通のさいころの各面を\(\,0\,～\,5\,\)とすればムダは減るでしょうけどね。
（この問題としては選択する文章が長くなるので「大きなお世話」でしょう。笑）

\(\,\large{1}\,\)は以上です。
配点が半分以上ありますので、見直しを大切にしておきましょう。

やはり長くなったので、というより\(\,\large{1}\,\)の問題数が多い（配点も大きい）ので、
ここで区切ろうと考えたのですが、
\(\,\large{2},\large{3}\,\)は平面図形なのでまとめるとすると、
学校選択問題が\(\,\large{3},\large{4}\,\)と同じなのでどうしよう。

と考えるより、\(\,\large{2}\,\)までをここで解説しておくことにします。

第２問作図と合同の証明

\(\,\large{2}\,\)は垂線の作図と三角形の合同の証明です。
基本問題\(\,2\,\)問なのでさっさと済ませます。

垂線の作図

(1)作図のポイントはコンパスの針をどこに刺して円を描くかです。
「頂点\(\,\mathrm{A}\,\)から垂線を引く」ので頂点\(\,\mathrm{A}\,\)に針を刺すことを考えましょう。
といっても垂線の作図と角の二等分線の作図は基本中の基本なので説明もいらないでしょう。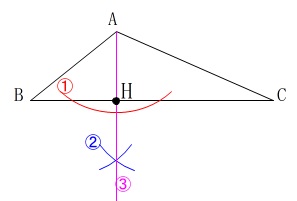
\(\,\color{red}{①}\,\)頂点\(\,\mathrm{A}\,\)から辺\(\,\mathrm{BC}\,\)と2点交わるように1つの円を描きます。
\(\,\color{blue}{②}\,\)点\(\,\mathrm{BC}\,\)との交点2つを中心とする同じ半径の円を描きます。
\(\,\color{magenta}{③}\,\)頂点\(\,\mathrm{A}\,\)と\(\,\color{blue}{②}\,\)の2つの円の交点とを結ぶ直線を描きます。

\(\,\color{magenta}{③}\,\)の直線と辺\(\,\mathrm{BC}\,\)との交点が求める点\(\,\mathrm{H}\,\)です。

三角形の合同の証明

\(\,(2)\,\)平行四辺形の性質を利用して内部の三角形の合同を証明します。

合同の証明も相似の証明も図の中で完成させておく、ということがポイントです。
このサイトのあちこちでいっていることですが、図の中で証明できていないことは日本語の文章にすることはなかなかできませんよ。

見逃してはいけないのはさりげなく書かれた条件、「平行四辺形\(\,\mathrm{ABCD}\,\)」ですね。
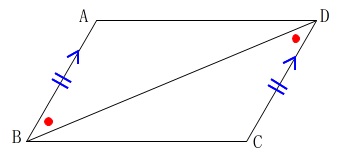対辺は平行で等しく、錯角が等しくなるので、仮定の垂線を条件に加えれば証明が終わっています。
（証明）
　\(\,\mathrm{△ABE}\,\)と\(\,\mathrm{△CDF}\,\)において
四角形\(\,\mathrm{ABCD}\,\)が平行四辺形であることから、
　\(\,\mathrm{ＡＢ＝ＣＤ}\,\)　（平行四辺形の対辺は等しい）　･･･①
　\(\,\mathrm{∠ABE=∠CDF}\,\)　（平行線の錯角は等しい）　･･･②
また、仮定から
　\(\,\mathrm{∠BEA=∠DFC=90^{\circ}}\,\)　･･･③
①②③より
　直角三角形の斜辺と1つの鋭角がそれぞれ等しい
ので
　\(\,\mathrm{△ABE}\,\)　≡　\(\,\mathrm{△CDF}\,\)
（証明終わり）