2020年度埼玉県公立高校一般入試の数学問題(第3,4問)と解説

2020年（令和2年）度に行われた埼玉県公立高校一般入試の数学問題と解説後半です。
後半といっても残り第3問,第4問の配点はそれほどありませんので終盤ですね。
ただし、一般入試の数学で差を付けるとすればこの2問なので本番で取りに行く準備（対策）をしておきましょう。

埼玉県一般入試\(\,2020\,\)年第\(\,3\,\)問相似,第\(\,4\,\)問関数の問題です。

⇒　2020年埼玉県一般入試数学第3問第4問の問題

\(\,\large{3}\,\)は比例式の計算と相似の活用問題です。
\(\,\large{4}\,\)は関数の問題で、文字設定と正方形の関係をつなげる問題です。

比例式と相似の活用問題

教科書にある相似の活用方法そのままの問題です。
比例式の計算は\(\,1\,\)年生の内容で、使う場面はたくさんありますが相似な図形に利用することが多いです。

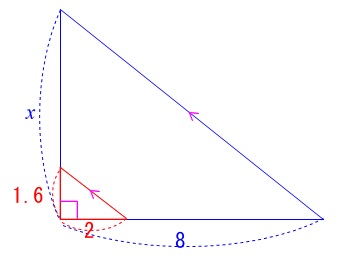
影と比例式

\(\,(1)\,\)太陽は遠いので平行な棒の先端の影の方向はすべて平行であると見なします。

長々と書かれた問題の条件を整理すると、
７行目の「ただし、」以降の２行に電柱と鉄棒が平行であることが書かれています。

よって影も平行になるので相似な三角形ができます。
これ以上説明は必要ないでしょう。

求める電柱の高さを\(\,x\,\)とすると比例式を解いて
　\(\begin{eqnarray}\displaystyle
1.6:x&=&2:8\\
2x&=&1.6\times 8\\
x&=&\frac{1.6\times 8}{2}\\
&=&\underline{　6.4　}　(　m　)
\end{eqnarray}\)

比例式の取り方は
　\(1.6:2=x:8\)
でも良いですよ。

三角定規の比を利用した関係式の立式

\(\,(2)\,\)今度は鉄塔の高さを求めますが、影の長さが分かりません。
先生の説明も長々と書かれているので読むのをあきらめたくなりますが、笑
与えあられた図が大きなヒントになっているので長さを書き込んで行けばすぐに求まります。

ただ、三角定規の比を思い出せるかどうかが問題になるだけです。
分かっているのは
　\(\,\mathrm{AA’=BB’=1.5}\,\)
　\(\,\mathrm{AB=50}\,\)
（単位は\(\,\mathrm{m}\,\)ですが省略します。）
という長さと角度です。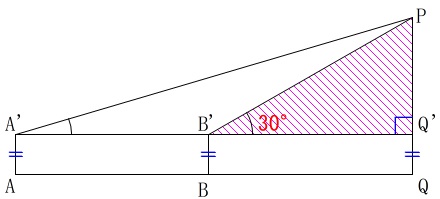図の\(\,\mathrm{△PB’Q’}\,\)は三角定規なのですべての角度が分かります。
すると\(\,\mathrm{△A’B’P}\,\)が二等辺三角形だと分かるので線分比もすべてわかります。
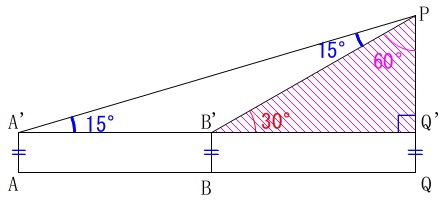線分\(\,\mathrm{PQ’}=x\,\)とすると、
三角定規の比\(\,(1:2:\sqrt{3})\,\)から
　\(\mathrm{PB’}=2x\)
二等辺三角形であることから
　\(\mathrm{A’B’=B’P}=2x\)
\(\,\mathrm{AB}=50\,\)なので
　\(\begin{eqnarray}\displaystyle
2x&=&50\\
x&=&25
\end{eqnarray}\)

また、目の高さ\(\,\mathrm{AA’=BB’=1.5}\,\)なので\(\,\mathrm{QQ’=1.5}\,\)を加えると、
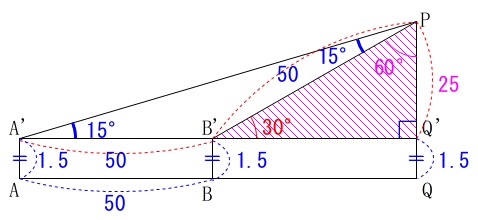鉄塔の高さは
　\(\begin{eqnarray}
\mathrm{PQ}&=&\mathrm{PQ’+Q’Q}\\
&=&25+1.5\\
&=&\underline{　26.5　}　(　\mathrm{m}　)
\end{eqnarray}\)

問題の図を利用できるのでかなり短時間で答えは出てくるでしょう。

ポイントは三角定規であることに気がついて、
分かる角度を書き込んで行くという基本的な作業（手を動かすこと）をするかしないかですね。

残るは\(\,\large{4}\,\)だけです。
あんまり余計な説明をしていると長くなるので先に進みます。

関数（文字設定と関係式の作り方）

\(\,(1)\,\)で直線を求め基本問題ですがこれを間違えていると\(\,(2)\,\)は解けません。
\(\,(2)\,\)は関数上の点の文字設定に慣れていればそれほど難しい問題ではありません。
ただ、注意することがあるので確認しておいてください。

　曲線は\(\displaystyle \,y=\frac{1}{2}\,x^2\,\)
　点\(\,\mathrm{A}\,\)の座標は\(\,(\,-6\,,\,18\,)\,\)
　点\(\,\mathrm{B}\,\)の座標は\(\,(\,4\,,\,8\,)\,\)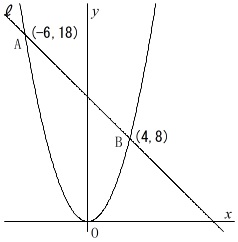これは変化しない\(\,(1)(2)\,\)に通じる条件です。

直線の求め方

(1)点\(\,\mathrm{A}\,\)と点\(\,\mathrm{B}\,\)を通る直線\(\,\ell\,\)の式を求めます。

直線が\(\,1\,\)次関数になるのは明らかなので、
　\(y=ax+b\)
とおいて\(\,\mathrm{A,B}\,\)の\(\,2\,\)点を代入して連立方程式でも良いですが、
\(\,2\,\)点が分かっているので傾きから求めます。

　\(\,(\,-6\,,\,18\,)\,\)
　\(\,(\,　4\,,\hspace{6pt}\,8\,)\,\)

傾きは変化の割合と同じです。
　\(\begin{eqnarray}\displaystyle
　a&=&\frac{8-18}{4-(-6)}\\
&=&\frac{-10}{10}=-1
\end{eqnarray}\)

これから求める直線は
　\(y=-x+b\)
とおけるので\(\,\mathrm{A,B}\,\)のどちらかを代入して切片を求めます。

点\(\,\mathrm{B}\,\)\(\,(\,4\,,\,8\,)\,\)を代入すると
　\(\begin{eqnarray}
(8)&=&-(4)+b\\
b&=&12
\end{eqnarray}\)

よって求める直線\(\,\ell\,\)の式は
　\(\underline{　y=-x+12　}\)

直線\(\,\ell\,\)は点\(\,\mathrm{A}\,\)\(\,(\,\color{red}{-6}\,,\,\color{blue}{18}\,)\,\)も通るので、
代入して成り立たなくては計算ミスしていますよ。
　\(\begin{eqnarray}
\color{blue}{18}&=&-(\color{red}{-6})+12\\
&=&18\end{eqnarray}\)
大丈夫です。
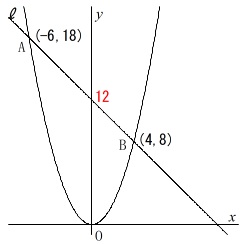グラフを見ても傾き、切片ともだいたい一致していることが大ざっぱですが確認できます。

座標の文字設定と正方形の性質

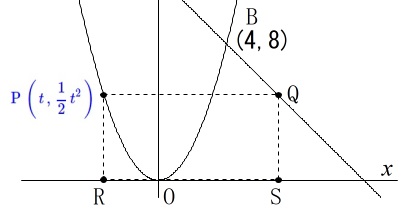
(2)点\(\,\mathrm{P\,,\,Q\,,\,R\,,\,S}\,\)が加わります。

　点\(\,\mathrm{P}\,\)は曲線上の点で\(\,\mathrm{A}\,\)から\(\,\mathrm{B}\,\)まで動く。
　点\(\,\mathrm{Q}\,\)は\(\,\mathrm{P}\,\)を通り\(\,x\,\)軸と平行な直線を引いたときの直線\(\,\ell\,\)との交点。
　点\(\,\mathrm{R}\,\)は\(\,\mathrm{P}\,\)から\(\,x\,\)軸に垂線を引いたときの\(\,x\,\)軸との交点。
　点\(\,\mathrm{S}\,\)は\(\,\mathrm{Q}\,\)から\(\,x\,\)軸に垂線を引いたときの\(\,x\,\)軸との交点。

四角形\(\,\mathrm{PRSQ}\,\)は長方形だということです。

その位置関係の1つを問題が与えてくれています。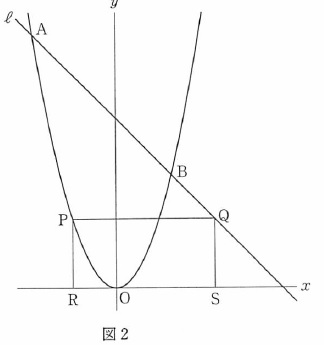
　\(\,①\,\)問題は長方形\(\,\mathrm{PRSQ}\,\)が正方形になるときの、点\(\,\mathrm{P}\,\)の座標を求めることです。

「点\(\,\mathrm{P}\,\)の\(\,x\,\)座標を\(\,t\,\)とおくと、」
とするように解答の書き始めは決められていますので迷うことはないでしょうけど、
長方形に何を条件として足せば正方形になるか、です。

ひし形の条件を長方形に足すと正方形になるので、
ひし形の条件
　\(\,4\,\)辺が等しい四角形
　対角線が直交する平行四辺形
のどちらかですが、対角線はちょっとややこしくなるので上の条件の辺ですね。
（長方形もひし形も正方形も平行四辺形ですよ。）

長方形（平行四辺形）だというのは分かっているので、
　\(\,\mathrm{PQ=PR}\,\)　または　\(\,\mathrm{PQ=QS}\,\)　または　\(\,\mathrm{RS=QS}\,\)
のどれか（となりあう\(\,2\,\)辺が等しい）を満たせば良いのです。

ここで気をつけておきたいのですが、
「すべて求めなさい。」
と問題が注意してくれているので２つ以上はあると考えておいた方が良いです。
（本当は注意書きがなくても可能性を探るのが応用になるのですが、この問題は親切です。）

後で分かりますが、普通に解いていけば答えが２つ出るので、
気をつけていない方が正解に近いかもしれませんけど。笑

答えを求める前に答えの個数だけでも推測しておきましょう。点\(\,\mathrm{P}\,\)を移動させて行くと長方形\(\,\mathrm{PRSQ}\,\)が正方形になるのはのは２つありそうです。
意味がないように見えるかもしれませんが、
これって問題を解くとき普通にやっていることです。
（私だけなのでしょうか？）

点\(\,\mathrm{P}\,\)は\(\,\mathrm{A}\,\)から\(\,\mathrm{B}\,\)まで動きます。
これは点\(\,\mathrm{P}\,\)が\(\,\mathrm{A}\,\)と\(\,\mathrm{B}\,\)に重なるときを除くと、
点\(\,\mathrm{Q}\,\)が点\(\,\mathrm{P}\,\)より右にあるということで、
点\(\,\mathrm{Q}\,\)の\(\,x\,\)座標の方が点\(\,\mathrm{P}\,\)の\(\,x\,\)座標より大きくなります。
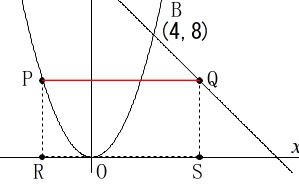どういうことかというと、
点\(\,\mathrm{Q}\,\)の\(\,x\,\)座標から点\(\,\mathrm{P}\,\)の\(\,x\,\)座標を引くと、
正の数になり、線分\(\,\mathrm{PQ}\,\)の長さになるということです。

ここまで見通しておくと、座標設定さえしておけば問題を解くのは簡単です。

　点\(\,\mathrm{P}\,\)の\(\,x\,\)座標を\(\,t\,\)とおくと、
点\(\,\mathrm{P}\,\)は点\(\,\mathrm{A}\,\)から\(\,\mathrm{B}\,\)まで動くので
　\(\color{blue}{\,-6\,≦\,t\,≦\,4\,}　･･･①\)

また、点\(\,\mathrm{P}\,\)は\(\,\displaystyle y=\frac{1}{2}x^2\,\)上の点だから、
　\(\color{blue}{\,\mathrm{P}\,\left(\,t\,,\,\displaystyle \frac{1}{2}\,t^2\,\right)}\,\)

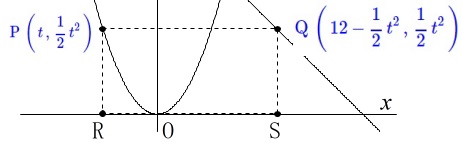
点\(\,\mathrm{Q}\,\)は直線\(\,\ell\,\)上の点で、\(\,y\,\)座標が点\(\,\mathrm{P}\,\)と同じなので、
\(\,y=-x+12\,\)に代入して\(\,x\,\)座標を求めると
　\(\begin{eqnarray}\displaystyle
\frac{1}{2}\,t^2&=&-x+12\\
x&=&12-\frac{1}{2}\,t^2
\end{eqnarray}\)
これから点\(\,\mathrm{Q}\,\)の座標は
　\(\color{blue}{\mathrm{Q}\displaystyle \,\left(\,12-\frac{1}{2}\,t^2\,,\,\frac{1}{2}\,t^2\,\right)}\,\)

点\(\,\mathrm{R}\,\)は点\(\,\mathrm{P}\,\)と\(\,x\,\)座標が同じで\(\,x\,\)軸上の点なので
　\(\,\color{blue}{\mathrm{R}\,(\,t\,,\,0\,)}\,\)
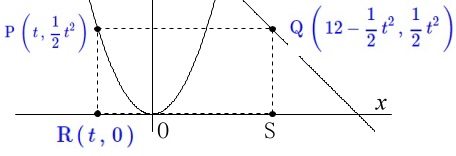点\(\,\mathrm{S}\,\)の座標も出せますが必要ありません。

正方形になるには隣り合う\(\,2\,\)辺が等しい長方形であれば良いので、
　\(\,\mathrm{PQ=PR}\,\)
となることが条件です。\(\,\mathrm{Q}\,\)の\(\,x\,\)座標の方が\(\,\mathrm{P}\,\)の\(\,x\,\)座標より大きいので、
線分\(\,\mathrm{PQ}\,\)の長さ（大きさ）は
　\(\displaystyle \mathrm{PQ}=\left(12-\frac{1}{2}\,t^2\right)-(\,t\,)　･･･②\)
\(\,\mathrm{PR}\,\)の長さは\(\,y\,\)座標の差ですが点\(\,\mathrm{P}\,\)の\(\,y\,\)座標の方が大きいので、
　\(\displaystyle \mathrm{PR}=\left(\frac{1}{2}\,t^2\,\right)-(\,0\,)=\frac{1}{2}\,t^2　･･･③\)

よって、\(\,②=③\,\)を満たす\(\,t\,\)を求めると
　\(\begin{eqnarray}\displaystyle
12-\frac{1}{2}\,t^2-t&=&\frac{1}{2}\,t^2\\
24-t^2-2t&=&t^2\\
-2\,t^2-2t+24&=&0\\
t^2+t-12&=&0\\
(t+4)(t-3)&=&0\\
t&=&-4\,,\,3
\end{eqnarray}\)

この2つは\(\,①\,\)の条件を満たしています。

このとき点\(\,\mathrm{P}\,\)座標は
　\(\displaystyle \underline{　\color{blue}{(\,-4\,,\,8\,)\,,\,\left(\,3\,,\,\frac{9}{2}\,\right)}　}\)

\(\,t\,\)の値を点\(\,\mathrm{P}\,\)を\(\,t\,\)で表した座標に代入するところを省略していますので自分で計算しておいてください。
※
この計算はミスしていないか、\(\,t\,\)の値を\(\,\mathrm{Q}\,\)に入れて\(\,\ell\,\)上にあるか確認するなど、
必ず見直すようにしておいた方が良いですよ。
　\(\,t=3\,\)のとき、\(\,\mathrm{P\,,\,Q}\,\)の\(\,y\,\)座標が\(\displaystyle \,\frac{9}{2}\,\)なので\(\,x\,\)座標は
　\(\begin{eqnarray}\displaystyle
\frac{9}{2}&=&12-x\\
x&=&12-\frac{9}{2}\\
&=&\frac{15}{2}\\
\end{eqnarray}\)
このとき点\(\,\mathrm{Q}\,\)は
　\(\displaystyle \color{blue}{\left(\,\frac{15}{2}\,,\,\frac{9}{2}\,\right)}\)
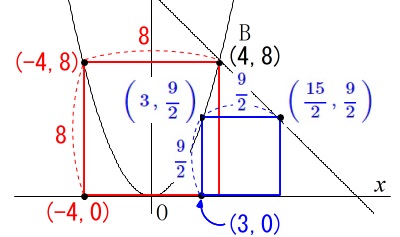確かに正方形になっています。　

三角形の面積比を一定にする点の座標

②は\(\,\mathrm{△BPQ:△OPQ=1:3}\,\)になるときの点\(\,\mathrm{Q}\,\)の座標を求めます。

この問題\(\,5\,\)点分あるのですが、やること（考え方）は\(\,①\,\)と同じですから見なくて良いです。笑
※
やることが同じというのは答えを推測しておくために手を動かすということですよ。

点\(\,\mathrm{P}\,\)は\(\,\mathrm{A}\,\)から\(\,\mathrm{B}\,\)まで動くのは\(\,①\,\)と同じで、
辺\(\,\mathrm{PQ}\,\)をどちらも底辺として持つので高さの比が\(\,1:3\,\)になれば良いだけです。

辺\(\,\mathrm{PQ}\,\)は\(\,x\,\)軸に平行なので高さは\(\,y\,\)座標、または\(\,y\,\)座標の差となることを確認しておきます。
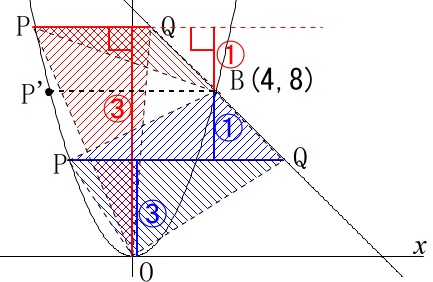点\(\,\mathrm{P}\,\)が\(\,\mathrm{P’}\,\)より上にあるときと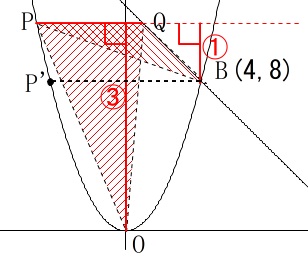
下にあるときで高さの取り方が変わります。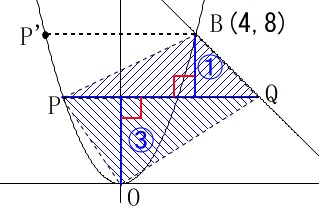それさえ分かれば答えは座標設定なしでも簡単にでます。

\(\,\mathrm{P}\,\)が\(\,\mathrm{P’}\,\)より上にあるときは、
\(\,\mathrm{Q}\,\)の\(\,y\,\)座標と\(\,\mathrm{B}\,\)の\(\,y\,\)座標の比が\(\,3:2\,\)なるときなので、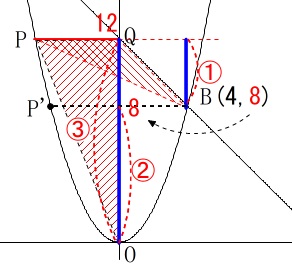
\(\,\mathrm{Q}\,\)の\(\,y\,\)座標は
　\(\begin{eqnarray}
y:8&=&3:2\\
2y&=&8\times 3\\
y&=&12
\end{eqnarray}\)
このとき、\(\,\mathrm{Q}\,\)の\(\,x\,\)座標は直線\(\,\ell\,\)の式が\(\,y=-x+12\,\)なので
　\(\begin{eqnarray}
12&=&-x+12\\
x&=&0
\end{eqnarray}\)

よって一つ目の\(\,\mathrm{Q}\,\)の座標は
　\(\,\underline{　(\,0\,,\,12\,)　}\,\)

\(\,\mathrm{P}\,\)が\(\,\mathrm{P’}\,\)より下にあるときは\(\,\mathrm{B}\,\)の\(\,y\,\)座標\(\,\color{red}{8}\,\)を\(\,1:3\,\)に分けるときなので、
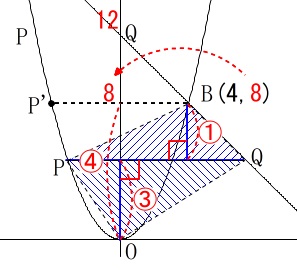\(\,\mathrm{Q}\,\)の\(\,y\,\)座標が\(\,\color{blue}{6}\,\)のときです。
直線\(\,\ell\,\)の式は\(\,y=-x+12\,\)なので
　\(\begin{eqnarray}
\color{blue}{6}&=&-x+12\\
x&=&6
\end{eqnarray}\)
よって、もう一つの\(\,\mathrm{Q}\,\)の座標は
　\(\,\underline{　(\,6\,,\,6\,)　}\,\)

答え　\(\,\underline{　(\,0\,,\,12\,)\,,\,(\,6\,,\,6\,)　}\,\)

\(\,①\,\)で設定した座標を使ってももちろん求めることはできます。
ただし、自分でやってください。笑
考え方は同じですし、計算もややこしいものではないのでそれほど時間はかかりませんよ。
求めるものが点\(\,\mathrm{P}\,\)ではなくて点\(\,\mathrm{Q}\,\)だということは忘れずに。

\(\,2020\,\)年度埼玉県一般入試数学の解説は以上です。
長くなったのでちょっと説明を省きましたが、\(\,\large{1}\,,\,\large{2}\,\)からもう一度見てください。

⇒　2020年(令和2年)度埼玉県公立高校一般入試の数学問題と解説（第1,2問）

応用問題ばかりではなく、基本問題がほとんどだと分かったでしょう。

⇒　埼玉県公立高校入試の数学（一般・学校選択）過去問と解説

対策するなら応用問題ばかりやって無駄な時間を過ごすのではなく、基本中心に反復した方がいいですよ。